
教学设想
李白的诗歌以他想像的丰富奇特,风格的雄健奔放,色调的瑰玮绚丽,语言的清新自然著称于世。“言出天地外,思出鬼神表”(皮日休)是对李白诗歌最准确的概括。学习《蜀道难》这首诗要引导学生认真疏导文句、熟读成诵,把握文章结构、章法,了解其主旨、寓意,从而深刻体会李白诗歌的特点,提高学生鉴赏诗歌的能力,以加深学生对诗人对祖国大好河山的热爱的认识。
课时安排
三课时。
第一课时
教学要点
解题,疏通文句,为赏析诗歌打好基础。
教学内容和步骤
《蜀道难》教案2
教学目的
20. 已知函数 ,数列
,数列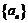 是公差为d的等差数列,
是公差为d的等差数列,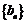 是公比为q
是公比为q
(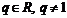 )的等比数列.若
)的等比数列.若



(Ⅰ)求数列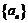 ,
,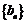 的通项公式;
的通项公式;
(Ⅱ)设数列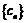 对任意自然数n均有
对任意自然数n均有 ,求
,求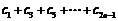 的值;
的值;
(Ⅲ)试比较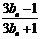 与
与 的大小.
的大小.
(Ⅰ) ∵  , ∴
, ∴ 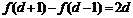 .
.
即 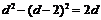 , 解得 d =2.
, 解得 d =2.
∴ 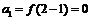 . ∴
. ∴ 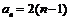 . ………………………………… 2分
. ………………………………… 2分
∵  , ∴
, ∴ 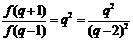 .
.
∵  , ∴
, ∴  .
.
又 , ∴
, ∴  .………………………………………… 4分
.………………………………………… 4分
(Ⅱ) 由题设知  , ∴
, ∴ .
.
当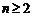 时,
时, 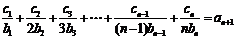 ,
,
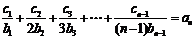 ,
,
两式相减,得 .
.
∴ 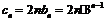 (
( 适合).…………………………… 7分
适合).…………………………… 7分
设T=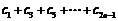 ,
,
∴ 
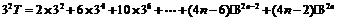
两式相减 ,得


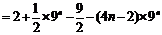
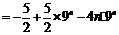 .
.
∴ 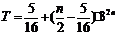 .…………………………………………………10分
.…………………………………………………10分
(Ⅲ)
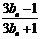
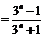
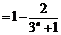 ,
, 
 .
.
现只须比较 与
与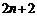 的大小.
的大小.
当n=1时,  ;
;
当n=2时,  ;
;
当n=3时, 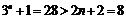 ;
;
当n=4时,  .
.
猜想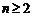 时,
时, . ………………………………13分
. ………………………………13分
用数学归纳法证明
(1)当n=2时,左边 ,右边
,右边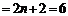 ,
, 成立.
成立.
(2)假设当n=k时, 不等式成立,即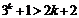 .
.
当n=k+1时, 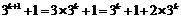
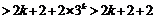
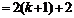 .
.
即当n=k+1时,不等式也成立.
由(1)(2),可知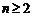 时,
时, 都成立.
都成立.
所以  (当且仅当n=1时,等号成立)
(当且仅当n=1时,等号成立)
所以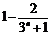
 .即
.即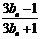
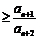 . …………… …… 16分
. …………… …… 16分
19. 已知函数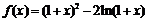 .
.
(Ⅰ)求f (x)的单调区间;
(Ⅱ)若当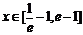 时,不等式f (x)<m恒成立,求实数m的取值范围;
时,不等式f (x)<m恒成立,求实数m的取值范围;
(Ⅲ)若关于x的方程 在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
在区间[0, 2]上恰好有两个相异的实根,求实数a的取值范围.
解:(Ⅰ)函数的定义域为(-1, +∞).…………………………………………… 1分
∵ 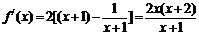 ,
,
由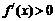 ,得x>0;由
,得x>0;由 ,得
,得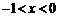 .………………… 3分
.………………… 3分
∴ f (x)的递增区间是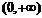 ,递减区间是(-1, 0).………………… 4分
,递减区间是(-1, 0).………………… 4分
(Ⅱ)∵ 由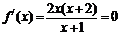 ,得x=0,x=-2(舍去)
,得x=0,x=-2(舍去)
由(Ⅰ)知f (x)在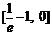 上递减,在
上递减,在 上递增.
上递增.
又 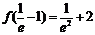 ,
, 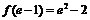 , 且
, 且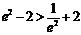 .
.
∴ 当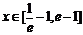 时,f (x)的最大值为
时,f (x)的最大值为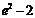 .
.
故当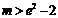 时,不等式f (x)<m恒成立.……………………………… 9分
时,不等式f (x)<m恒成立.……………………………… 9分
(Ⅲ)方程 ,
, 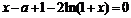 .
.
记 ,
,
∵ 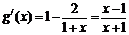 ,
,
由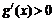 ,得x>1或x<-1(舍去). 由
,得x>1或x<-1(舍去). 由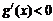 , 得
, 得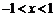 .
.
∴ g(x)在[0,1]上递减, 在[1,2]上递增. ………………………………12分
为使方程 在区间[0, 2]上恰好有两个相异的实根,
在区间[0, 2]上恰好有两个相异的实根,
只须g(x)=0在[0,1]和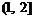 上各有一个实数根,于是有
上各有一个实数根,于是有
∵  , ………………………………14分
, ………………………………14分
∴ 实数a的取值范围是 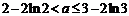 . ……………………… 16分
. ……………………… 16分
18. 某机床厂今年初用98万元购进一台数控机床,并立即投入使用,计划第一年维修保养、费用12万元,从第二年开始,每年的维修、保养修费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利总额为y元。
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利?
(3)使用若干年后,对机床的处理有两种方案:①当年平均盈利额达到最大值时,以30万元价格处理该机床;②当盈利额达到最大值时,以12万元价格处理该机床。问哪种方案处理较为合理?请说明理由。
解:解:(1)y= -2x2+40x-98,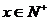 ………………4分
………………4分
(2)由-2x2+40x-98>0
解得, ,且
,且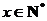 ,
,
所以
故从第三年开始盈利。 ………………10分
(3)由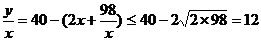 ,当且仅当x=7 时“=”号成立,
,当且仅当x=7 时“=”号成立,
所以按第一方案处理总利润为 (万元)……12分
(万元)……12分
由y= -2x2+40x-98= -2-- (x-10)2+102 ,
,
所以按第二方案处理总利润为102+12=114(万元) ………………14分
由于第一方案使用时间短,则选第一方案较合理. …………16分
17.在数列 中,
中, ,
, ,
, ,
,
(Ⅰ)证明:数列 是等比数列;
是等比数列;
(Ⅱ)设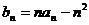 ,求数列
,求数列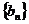 的前n项和
的前n项和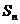 ;
;
解:(Ⅰ)证明:由题设 ,
,
|
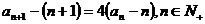
|
 ∴
∴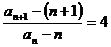
|
 是首项为1,且公比为4的等比数列
是首项为1,且公比为4的等比数列
|
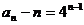
|

∴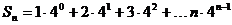 ……①
……①
|
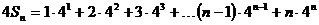 ……②
……②
|
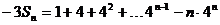
|
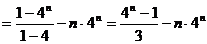
∴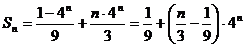
|
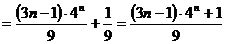
16. 已知向量 a = (cos x,sin x),b = (-cos x,cos x),c = (-1,0)
(I) 若 x = ,求向量 a、c 的夹角;
(II) 当 x∈[,] 时,求函数 f (x) = 2a·b + 1 的最大值。
解:解:(I) 当 x = 时,cos <a,c> = ………… 1分
= ………… 2分
= -cos x = -cos = cos ………… 3分
∵ 0≤<a,c>≤p, ………… 4分
∴ <a,c> = ………… 6分
(II) f (x) = 2a·b + 1 = 2 (-cos 2 x + sin x cos x) + 1 ………… 7分
= 2 sin x cos x-(2cos 2 x-1) ………… 8分
= sin 2x-cos 2x ………… 9分
= sin (2x-) …………10分
∵ x∈[,],∴ 2x-∈[,2p], ………… 11分
故 sin (2x-)∈[-1,] ………… 12分
∴ 当 2x-= ,即 x = 时,f (x)max = 1 ………… 14分
15.在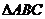 中,
中, ,
, .
.
(Ⅰ)求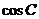 ;
;
(Ⅱ)设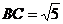 ,求
,求 的值.
的值.
解:解:(Ⅰ)由 ,
,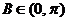 ,得
,得 ………1分
………1分
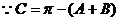 ,
,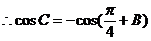 ,
………………3分
,
………………3分
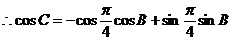 ………………6分
………………6分
即 .
………………7分
.
………………7分
(Ⅱ)根据正弦定理得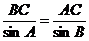 ,
,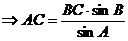 , ………………9分
, ………………9分
由 ,得
,得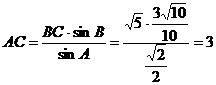 , ………………12分
, ………………12分
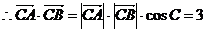 .
………………14分
.
………………14分
14. 下列说法:①当 ;②
;②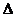 ABC中,
ABC中,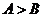 是
是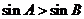 成立的充要条件;③函数
成立的充要条件;③函数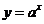 的图象可以由函数
的图象可以由函数 (其中
(其中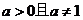 )平移得到;④已知
)平移得到;④已知 是等差数列
是等差数列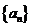 的前
的前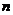 项和,若
项和,若 ,则
,则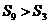 .;⑤函数
.;⑤函数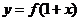 与函数
与函数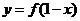 的图象关于直线
的图象关于直线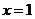 对称。其中正确的命题的序号为 ②
③ ④
对称。其中正确的命题的序号为 ②
③ ④
13. 已知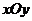 平面内一区域
平面内一区域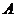 ,命题甲:点
,命题甲:点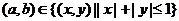 ;命题乙:点
;命题乙:点
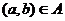 .如果甲是乙的充分条件,那么区域
.如果甲是乙的充分条件,那么区域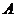 的面积的最小值是
2.
的面积的最小值是
2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com