
3.掌握一次函数的概念和性质;
2.直线的斜率和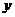 轴上的截距;
轴上的截距;
1.一次函数的性质与图像;
2.2.1一次函数的性质与图像 学案
[预习要点及要求]
引导学生对一次函数和正比例函数小结: 
⑴定义; ⑵图象(形状、画法); ⑶性质。
⒈一次函数图象的形状:
⑴电脑显示:我们画过的函数y=x,y=x+0.5,和作业中画过的函数y=4x-1,y=4x+1的图象。
⑵问:这几个函数分别是什么函数?它们的图象分别是什么图形?
⑶观察、讨论与归纳:所有一次函数的图象都是一条直线。
⒉一次函数的图象的画法:
⑴问:我们知道一次函数的图象是一条直线,那么今后我们画一次函数的图象是否还是通过描出许多点再连线呢?有没有简捷的方法呢?
⑵讨论:两点确定一条直线,画一次函数的图象只需描出两点,再过这两点作直线。
⑶结论:一次函数图象的画法──“两点法”。
⒊取两适当点画正比例函数的图象:
⑴问题:取怎样的两点画函数y=0.5x,y=-0.5x的图象合适呢? (学生可以自学看书)
⑵讨论:计算简便,描点方便。
⑶画图:师生分别画图。
⑷小结:画正比例函数的图象时,常选取(0 ,0)、(1,k)两点连线。正比例函数的图象必过原点。
,0)、(1,k)两点连线。正比例函数的图象必过原点。
⒋取两适当点画一次函数的图象:
⑴问题:怎样取合适的两点画一次函数y=kx+b 的图象呢?
⑵自学:学生自学例题1; (电脑动画显示函数图象的作图过程)
⑶思考 与讨论:
与讨论:
①横坐标为0点在---上,纵坐标为0点在---上。
②在y=kx+b中,当x=0时,y=---;当y=0时,x=---。
③画一次函数的图象,常选取(0,--)、(--,0)两点连线。
⑷小结:
画一次函数y=kx+b图象的一般步骤:
①在横轴上取点(-b/k,0) ,在纵轴上取点(0,b);
,在纵轴上取点(0,b);
②过这两点作直线;
⒌正比例函数的 性质:
性质:
⑴问题:正比例函数有着特殊形状,那么它有什么性质呢?
⑵观察、思考与讨论:在坐标平面内,对于直线y=0.5x与y=-0.5x,点的横坐标增大时,纵坐标怎样变 化?(引导学生分别从列表、图象上点的升降分析)
化?(引导学生分别从列表、图象上点的升降分析)
⑶归纳:引导学生归纳正比例函数的性质。
⒍一次函数的性质:
⑴思考:一次函数y=kx+b又有什么性质呢?
⑵类比与归纳:引导学生用总结y=kx的性质的方法,总结一次函数y=kx+b 的性质。
已知函数的解析式,我们可以画出函数的图象,那么一次函数(包括正比例函数)的图象是什么形状呢?它们又有什么性质呢?
(教师板书课题──一次函数的图象和性质)
什么叫一次函数?什么叫正比例函数?它们有何关系?
(学生回答后教师板书定义式)
创设情境,引入课题 
前面我们己学习了一次函数的概念,一般地,如果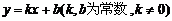 ,那么
,那么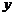 叫
叫 的一次函数。特别地:当
的一次函数。特别地:当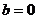 时,一次函数就变成了正比例函数
时,一次函数就变成了正比例函数 。
。
在同一直角坐标系中投影出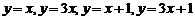 的函数图象,让学生观察它们的图象都是直线并引入课题。
的函数图象,让学生观察它们的图象都是直线并引入课题。
所有的一次函数的图象都是直线。因此要画一次函数的图象--一条直线,就没有必要把所有的点都描出来,只要描出两个点就可以了,因为两个点确定一条直线。利用这个结论,我们可以更快地作出一次函数的图象,并对它的性质进行研究。
描点画图,归纳画法
[过渡]下面我们一起来画首先共同画出正比例函数 与
与 的图象。并由此归纳出正比例函数
的图象。并由此归纳出正比例函数 的图象为过
的图象为过 和
和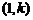 两点的直线。
两点的直线。
观察图象、研究性质
然后提出问题1:让学生自己画图,研究正比例函数有何性质?即正比例函数 中,
中,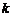 对函数图象有何影响?并填写实验报告(课前印好发给学生,或者学生在网络上填写)。
对函数图象有何影响?并填写实验报告(课前印好发给学生,或者学生在网络上填写)。
研究问题1时,我首先通过几何画板与学生共同归纳正比例函数 与
与 的图象性质,特别是
的图象性质,特别是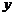 随
随 的变化趋势。
的变化趋势。
打开几何画板,进行演示。点在直线上运动,对应着 轴上射影(用红点显示)、
轴上射影(用红点显示)、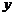 轴上的射影(用绿点显示)同时运动。从左到右拖动红点,使点的横坐标从小到大变化,红点的运动引起绿点的运动,绿点的运动又使点的纵坐标发生变化。在
轴上的射影(用绿点显示)同时运动。从左到右拖动红点,使点的横坐标从小到大变化,红点的运动引起绿点的运动,绿点的运动又使点的纵坐标发生变化。在 演示的同时,启发学生注意观察坐标的变化并得到:对于
演示的同时,启发学生注意观察坐标的变化并得到:对于 ,
,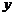 随
随 的增大而增大;对于
的增大而增大;对于 ,
,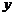 随
随 的增大而减小。
的增大而减小。
然后把学生分成两人一组,进行继续用几何画板研究其它正比例函数的性质,并把结论发到网络的“展示区”上。填写实验报告如下:
实验报告: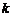 对正比例函数
对正比例函数 的图象的影响。
的图象的影响。
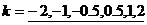
|
|
解析式 |
图象示意图 |
图象所在的象限 |
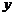 随 随 的变化趋势 的变化趋势 |
 |
 [来源:ZXXK] [来源:ZXXK] |
在刚才所画  直 直 角坐标系中分别画出,图象如下所示。 角坐标系中分别画出,图象如下所示。 |
1,3象限 |
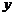 随 随 的增大而增大 的增大而增大 |
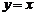 |
1,3象限 |
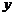 随 随 的增大而增大 的增大而增大 |
||
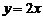 |
1,3象限 |
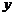 随 随 的增大而增大 的增大而增大 |
||
 |
 |
2,4象限 |
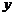 随 随 的增大而减小 的增大而减小 |
|
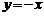 |
2,4象限 |
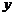 随 随 的增大而减小 的增大而减小 |
||
 |
2,4象限 |
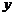 随 随 的增大而减小 的增大而减小 |
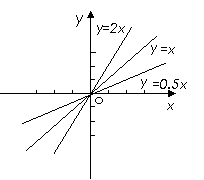

在实验报告的基础上,让学生利用几何画板动手实验:拖动点N,让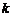 的值连续变化,引导学生观察正比例
的值连续变化,引导学生观察正比例 的图象的变化并归纳出它的性质:
的图象的变化并归纳出它的性质:
当 时,图象在1,3象限,
时,图象在1,3象限,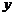 随
随 的增大而增大;
的增大而增大;
当 时,图象在2,4象
时,图象在2,4象 限,
限,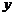 随
随 的增大而减小。
的增大而减小。
为了达到及时巩 固的效果,归纳之后进行练习1。练习1结合课本练习,培养学生
固的效果,归纳之后进行练习1。练习1结合课本练习,培养学生 的数形结合能力。
的数形结合能力。
第1、2、3题都是由函数解析式判断图象的性质;
第4题是由函数图象性质判断函数的解析式。
并通过填空、选择的形式,让学生进行自我评 价。(1)做完练习1后,会显示每道题目的答案正确与否,同时根据
价。(1)做完练习1后,会显示每道题目的答案正确与否,同时根据 学生练习完成的情况,给出鼓励性
学生练习完成的情况,给出鼓励性 评价;(2)老师可以对全体学生练习情况进行即时统计,从而进行针对性教学;(3)练习完成的好的学生可以进入英雄榜,让学生更乐于学习。
评价;(2)老师可以对全体学生练习情况进行即时统计,从而进行针对性教学;(3)练习完成的好的学生可以进入英雄榜,让学生更乐于学习。
类比联想、探索性质
首先学习例3:在同一直角坐标系中画出 与
与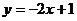 的图象。在画图的过程中利用表格(如下):
的图象。在画图的过程中利用表格(如下):
|
解析式 |
与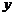 轴的交点 轴的交点 |
与 轴的交点 轴的交点 |
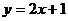 |
 |
 |
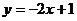 |
 |
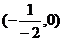 |
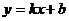 |
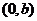 |
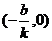 |
归纳出一 次函数
次函数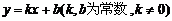 为过
为过 和
和 两点的直线。
两点的直线。
然后提出问题2:讨论一次函数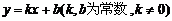 中,
中, 对函数图象有何影响?
对函数图象有何影响?
在解决问题2时,首先抓住正比例函数是一次函数的特殊情况,让学生了解这一关系并从中直接得出一次函数性质。
然后利用网络让学生动手实验:
先固定 的值,拖动滑板,让
的值,拖动滑板,让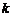 的值连续变化,观察图象的变化,归纳出一次函数
的值连续变化,观察图象的变化,归纳出一次函数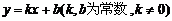 的性质:
的性质:
当 时,
时,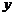 随
随 的增大而增大;
的增大而增大;
当 时,
时,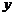 随
随 的增大而减小。
的增大而减小。
再固定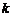 的值,拖动滑板,让
的值,拖动滑板,让 的值连续变化,观察图象的变化,归纳出
的值连续变化,观察图象的变化,归纳出 的变化引起图象变化规律:一次函数
的变化引起图象变化规律:一次函数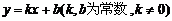 图象与
图象与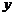 轴的交点为
轴的交点为 。
。
练习反馈、巩固性质
为了加强学生对“数”与“形”的双向沟通,我在课本练习基础上设计了一些 “由数到形”及“由形到数”的题目,供学生练习。练习2采用
“由数到形”及“由形到数”的题目,供学生练习。练习2采用 题组分层次教学,先后通过A、B、C三组(9题)进行练习,每组题均由浅入深,各有针对性。
题组分层次教学,先后通过A、B、C三组(9题)进行练习,每组题均由浅入深,各有针对性。
A组题为只考虑一个常数 的题目;
的题目;
B组题为只考虑一个常数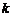 的题目;
的题目;
A、B两组题为必做题;
C组综合考虑两个常数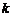 与
与 的题目,C组题为选做题。
的题目,C组题为选做题。
这样遵循循序渐进的规律进行题组教学,顾及到了各个层次的学生,达到了预期的目的。
小结归纳,揭示 规律
规律
先由学生归纳,再由老师总结,培养学生的归纳能力。
(1)正比例函数 的图象的画法:过原点与点
的图象的画法:过原点与点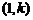
 的直线即所求的图象;
的直线即所求的图象;
(2)一次函数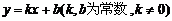 图象的画法:在
图象的画法:在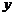 轴上取点
轴上取点 ,在
,在 轴上取点
轴上取点 ,过这两点的直线即所求的图象;
,过这两点的直线即所求的图象;
(3)正比例函数 与一次函数
与一次函数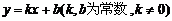 的性质。
的性质。
“实践探究、启发引导、归纳概括” 的引导探究法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com