8．★★★★(教材1.1例1变式)从某大学中随机选取8名女大学，其身高与体重的数据如下：

(1)不画散点图判断体重与身高是否具有相关关系；

(2)如果体重与身高具有相关关系，求回归直线方程，并预测身高为172cm的女大学生的体重.

实践演练

7．★★★(教材1.1例1变式)一位母亲记录了她儿子3岁到9岁的身高，数据如下：

由此建立了身高与年龄的回归模型:

y=73.93+7.19x，她用这个模型预测儿子10岁时的身高，则下列叙述正确的是(　)

A．她儿子10岁时的身高一定145.83cm

B．她儿子10岁时的身高在145.83cm 以上

C．她儿子10岁时的身高在145.83cm 左右

D．她儿子10岁时的身高在145.83cm 以下

6．★★★在利用线性回归模型进行预报时，有以下四种说法：

①样本数据是来自那个总体，预报时也仅适用于这个总体；

②线性回归模型具有时效性；

③建立模型时自变量的取值范围决定了预报时模型的适用范围，通常不能超出太多；

④在回归模型中，因变量的值不能由自变量的值完全确定.

其中说法正确的有　　　　.

(只填你认为正确说法的序号)

变式活学

5．★★同一资料，如果将作为自变量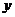，作为因变量，得回归系数；将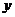作为自变量，因变量，得回归系数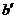，则相关系数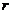与的关系是　　　　　

4．★作一个两个变量散点图的主要目的是

3．★★★由一组样本数据，，

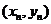，得到回归直线方程，那么下列说法中不正确的是(　)

A．直线必经过点

B．直线至少经过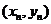点，，，中的一个点

C．直线的斜率为

D．直线的纵截距为

2．★★在画两个变量的散点图时，下面叙述正确的是(　)

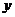A．预报变量在轴上，解释变量在轴上

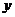B．解释变量在轴上，预报变量在轴上

C．可以选择两个变量中任意一个变量在轴上

D．可以选择两个变量中任意一个变量在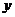轴上

1．★下列现象属于相关关系的是(　)

A．家庭收入越多，消费也越多　

B．圆的半径越大，圆的面积越大

C．气体体积随温度升高而膨胀，随压力加大而减小

D．在价格不变的条件下，商品销售量越大销售额也越大

3.1回归分析的基本思想及其初步应用(1)

双基再现

3.1回归分析的基本思想及其初步应用

A卷(课堂针对训练一)