5．A．f(x)=(x-a)(x-b)-2　 ∴令g(x)=(x-a)(x-b)

f(x)=0方程的根即为f(x)=h(x)交点横坐标　 α<a<b<β

4．B．画出|f(x)|和g(x)的图象即可。

3．D．见函数图象(一)解答题10题(1)问，方法相同。

2．D．　 的图象向右平移1个单位长度。

1．B．|log_ax|>1　 ∴log_ax>1或loga^x< -1　　

log_ax>1在上恒成立　 ∴

loga^x< -1在上恒成立，则 　　∴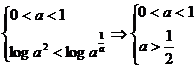

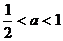
10．解：(1)f(0)=f(0)f(0)　　 f²(0)=f(0)

　　 ∴f(0)=0或f(0)=1

若f(0)=0　 对任意x，有f(x+0)=f(x)f(0)

∴f(x)=0还与x<0, f(x)>1矛盾

∴f(0)=1

若x>0, -x<0, f(-x)>1

f(x-x)=f(x)f(-x)　　 f(0)=f(x)·f(-x)

又∵f(0)=1　　 ∴

又∵f(-x)>1　 0<f(x)<1　 ∴x∈R, f(x)>0

设x₁>x₂　

∵x₁>x₂　 ∴x₁-x₂>0

0<f(x₁-x₂)<1　 ∴f(x₂)<f(x₂)　

∴y=f(x)在R上单调递减

(2)∵y=f(x)单调　　 ∴f(a_n+1)=f(2+a_n)　 ∴a_n+1=a_n+2　　 ∴a_n+1-a_n=2

∴{a_n}是以a₁=f(0)=1为首项，公差为Z的等差数列

∴a_n=a₁+(n-1)d=1+(n-1)×2=2n-1

b₁+b₂+…+b_n

=

函数图象性质(二)答案

9．略

8．a^x-b^x>0 即 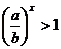且，依题意f(x)在(0,+∞)上是增函数，且f(1)=0, f(1)=lg(a-b)

令lg(a-b)=0　 ∴a-b=1

7．分a>1和0<a<1，分别运用图象交换的方法作函数y=|a^x-1|以及y=2a的图象

6．f(x)=a|x-b|+2　 对称轴x=b　 b≤0 　a<0