3．碳酸钠和碳酸氢钠与酸的反应

本实验也可采用下述方法进行：

取相同式样的100 mL细口瓶两只，各注入25 mL 1．0 moL·L^－1 HCl溶液．再取两只气球，一只装入1.0 g无水碳酸钠，另一只装入1.0 g碳酸氢钠，分别套在两只细口瓶的口上．

实验时，掀起两只气球，使里面的固体全部落到细口瓶里的盐酸中，比较反应的剧烈程度，碳酸氢钠的反应剧烈得多，碳酸氢钠放出的气体也比碳酸钠多．

(1)钠的物理性质及钠跟水的反应

新切开的钠的断面是光亮的银白色，易跟氧起反应，但产物较复杂，如氧化钠(Na₂O)、过氧化钠(Na₂O₂)等．

金属钠跟水反应生成氢气的实验，用拇指堵住试管口倒放入烧杯中，这样的操作对学生来讲，不熟练可能会使一部分空气进入试管．所以在正式做收集气体的实验之前，教师可安排学生练习几次放入试管的操作．如果操作还是有困难，可用一个与试管口大小合适的橡皮塞堵住试管口，放入水中后再拔去橡皮塞．本实验也可以用水槽代替烧杯，这样口径比较大，操作方便．

注意在实验时不能取用较大的钠块．这是因为钠的性质很活泼，它跟水反应时放出大量的热，甚至能使周围的水沸腾，因此钠同时也跟水蒸气反应．如果在水面上游动的钠被容器壁上的油污粘住，不能游动，放出的热不易扩散，会使氢气着火燃烧，甚至还会发生小爆炸，使生成的氢氧化钠飞溅出来．

(2)钠与氧气的反应

在做钠与氧气反应的实验时，为了保证倾斜的空气能够流通，玻璃管不能太细，而且装入玻璃管中的钠粒不能太大．待玻璃管中的钠受热溶化并开始燃烧时，稍稍倾斜玻璃管即可看到燃烧后由白色变为黄色的过程．实验时如果没有太粗的玻璃管，也可用去底的试管代替．注意本实验中所用的钠块，应去掉其表面的氧化物，否则燃烧时会使试管壁显黑色，影响对实验现象的观察．

2．碳酸氢钠受热分解

碳酸氢钠粉末在试管中应铺平些，这样受热比较均匀，分解也比较完全，澄清的石灰水变浑浊后，应将盛石灰水的试管移去，因为若通入过多的二氧化碳，会使生成的碳酸钙变成碳酸氢钙而溶解于水中，使浑浊现象消失．

当实验结束时，一定要先移去装有石灰水的烧杯，再熄灭酒精灯，以防止水倒流，使试管炸裂．

2．地理计算综合题的复习备考策略

近年高考试题中的地理综合计算题，大致可分为两种类型。一是提供信息材料运用教材中相关地理概念、规律和原理加以计算；二是提供信息材料和计算公式(教材中未涉及的计算方法)来计算。针对这一高考命题思想，我们在复习备考中应抓好以下几方面的工作。

⑴归纳整理教材中的相关地理计算原理。运用地理规律、原理，通过一定的运算，求出各种地理数据，是学习地理应掌握的基本技能之一。在现行中学地理教材中，相关地理计算的规律、原理还是较多的，同学们在复习备考的过程中，应归纳整理相关的地理计算原理，搞清各种计算方法。例如：①比例尺的计算，包括比例尺的三大要素的相互换算、经纬网图中实际距离的计算等；②等高线地形图中的高度计算，包括陡崖的相对高度计算、水库大坝高度计算等；③温度计算，包括利用气温递减率计算某一高度的气温、利用地温递增率计算某一深度的地温等；④时间的相关计算，包括地方时、时区、区时计算和逆向的根据时间推算经度，两天不同日期范围计算等；⑤昼夜长短的相关计算；包括昼长与日出、日落时间的相互换算、光照图中的昼长计算、极昼极夜的纬度推算等；⑥正午太阳高度的相关计算，包括正午太阳高度的计算、建筑物合理间距的计算、根据正午太阳高度推算纬度等；⑦人口密度计算；⑧人口出生率、死亡率和自然增长率的计算；⑨森林覆盖率计算；⑩各类构成比例的计算，包括农业产值构成计算、工业产值构成计算、能源消费构成计算等等。

⑵强化材料信息的处理能力。从各类资料中认定和提取地理信息，并对其做出判断和思考，是目前高考地理的十大能力要求之一。近年的高考地理计算综合题充分反映了这一能力要求趋向，或以文字材料、或以图像材料、或以表格材料展现地理信息，要求考生从中提取有效的解题信息，再根据相关的地理计算规律、原理或公式加以计算，得出正确的结论。在备考阶段，对考生而言，则应以近年高考试题为样本，加强相关试题的适应性训练，从中寻找一些规律性的材料信息的处理方法和解题方法，以提高自身的解题能力

1．各类“地理计算”的关键知识与思路：

3．其他计算

2．与地球运动有关的计算

①时区、区时和地方时的计算

Ⅰ地方时：不同经度的时间。掌握东加西减、东早西晚的原则，每相差15度，时间上相差1小时，4分钟相差1度。根据已知时间求经度时，注意用时间的早晚来确定经度的东西方位。 Ⅱ区时：各地没有特殊说明情况下使用的时间。先掌握时区的计算，区时的计算方法与地方时的原则相同，每相差一个时区时间相差一个小时。注意地方时与区时的相互转换。 Ⅲ标准时：各国统一使用的时间。绝大部分国家只有一个标准时，多采用这个国家东部时区的区时，也有采用半区时的国家，如印度等；少数大国有两个标准时，如中国、美国、俄罗斯等。注意一个国家的任何地区，所使用的时间都为标准时，除非有特别说明是所在时区的区时或所在经线的地方时时例外。 Ⅳ北京时间：我国全国统一使用的时间，即东八区的区时，东经120度的地方时。注意北京时间不等于北京地方时，在有关日出日落时间的题目中多采用的是地方时。 ⑵不同日期的分界线及范围的计算

①日期的变换有两种变换，即自然变换和人为变换。

自然变换是某地区时间为24点时，其日期事实上已是新的一天。 人为变换是指日界线，过日界线日期变换的原则是向东减一天，向西加一天。东、西十二区这两个半时区，在区时上是相同的，但日期上相差一天，东十二区是全球时间最早的地方，而西十二区是全球时间最晚的地方，即全球最东和最西的地方。 ②全球总是被两条经线分割为两个日期，分割日期的经线分别是日界线和地方时为0时的经线，这两条经线可以重合，当二者重合的一瞬间，全球只有一个日期。注意真实的情况下，日界线和180度经线并非完全重合，在俄罗斯、阿留申群岛、南太平洋等地有明显弯曲。 　　 今天范围的计算，采用的多为地方时。180度时间如果为T，那么地球上新的一天范围为T/124，旧的一天范围为(24－T)/24。也可以把T转化为北京时间Q，即Q＝T－4。 如果使用的区时，那么新的一天范围可用时区数表示，时区数为180度经线的区时T+0.5个时区。注意一般情况下没有24点，它可表示第二天的0点。 ⑶正午太阳高度的计算 ①正午太阳高度的计算公式是：H＝［90°－β(当地纬度和太阳直射点纬度)］，其中β的求采用同一半球相减、不同半球相加的原则，永远取正值。 ②利用垂直物体的日影计算：cotH＝影长/物体长度。 ③太阳能热水器的采光面与楼房顶面的夹角＝β(β同①) ④南北半球中纬度地区楼房间隔L的计算：L＝楼高×cotH°( H°即当地全年最小的正午太阳高度角，北半球为冬至日的正午太阳高度，南半球为夏至日的正午太阳高度)。在楼房布局时建议采用东北－西南向或西北－东南向。 ⑤一个地区年正午太阳高度最大差值： 赤道地区是23°26’ 南北半球热带地区介于23°26’和46°52′之间，具体度数是(当地纬度+23°26′)。 南北半球温带地区是46°52′。 南北半球寒带地区是46°52′，但也可以当作当地最大正午太阳高度的数值。 ⑷昼夜长短的计算

①可以利用一个地区昼弧所跨的经度范围来计算，方法是在日照图上某条纬度与晨昏线有两上交点，两点之间在昼半球的部分即是白昼的时间。 　　 ②可以利用已知的日出和日落时间来求算。方法是：白昼长＝2×(12－日出时间)或白昼长＝2×(日落时间－12)。 　　 ③同一半球相同纬度地区昼长相同。而南北半球相同纬度地区的昼夜长短相反，如北纬40度的昼长是15时，那么南纬40度的地区夜长为15时。 ④注意极昼区、极夜区的昼长分别是24时和0时。赤道地区的昼长永远是12时。

1．地图的计算

⑴两地之间距离的计算

两地之间距离的计算主要有两种类型：一是已知比例尺求实际距离，只要量出所求两点之间的图上距离再用公式(实际距离=图上距离/比例尺)进行计算即可，需要注意的是单位一定要一致。二是通过经度或纬度差来进行计算，纬度差1度的经线长约为111千米，经度差1度的纬线长约等于111千米×cosφ(φ为所求地的纬度)。

⑵相对(断崖)高度的计算

断崖在等高线地形图上表现为若干条等高线的重叠处，其顶部的海拔高度应为几条重叠等高线中海拔最大值或之上，而底部的海拔高度应为几条重叠等高线中海拔最小值或之下，同时通过归纳得出，断崖的顶部和底部的相对高度H为：d(n-1)≤ H ＜ d(n+1) (其中d为等高距，n为重叠的等高线条数)

16.(18分)如图所示为某种弹射装置的示意图，光滑的水平导轨MN右端N处与水平传送带理想连接，传送带长度L=4.0m，皮带轮沿顺时针方向转动，带动皮带以恒定速率v=3.0m/s匀速传动。三个质量均为m=1.0kg的滑块A、B、C置于水平导轨上，开始时滑块B、C之间用细绳相连，其间有一压缩的轻弹簧，处于静止状态。滑块A以初速度v0=2.0m/s沿B、C连线方向向B运动，A与B碰撞后粘合在一起，碰撞时间极短，可认为A与B碰撞过程中滑块C的速度仍为零。因碰撞使连接B、C的细绳受扰动而突然断开，弹簧伸展，从而使C与A、B分离。滑块C脱离弹簧后以速度vC=2.0m／s滑上传送带，并从右端滑出落至地面上的P点。已知滑块C与传送带之问的动摩擦因数μ=0.20，重力加速度g取10m／s2。求 (1)滑块c从传送带右端滑出时的速度大小；　

(2)滑块B、C用细绳相连时弹簧的弹性势能Ep；

(3)若每次实验开始时弹簧的压缩情况相同，要使滑块C总能落至P点，则滑块A与滑块B碰撞前速度的最大值Vm是多少?

15．(12分)如图所示，质量 m =1kg的物块(可视为质点)在水平恒力F= 10N作用下，从水平面上 A点由静止开始运动，运动2s后再加一反向的水平恒力=16N，问再经多少时间物块运动到B点，且A、B两点间的距离为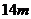，已知物块与水平面间的动摩擦因数μ=0.20。(g=10m/s2)

14．(12分)如图所示，固定的光滑竖直圆形圆形轨道，其半径为R，在它的底端静止一个质量为m小球，现给小球一个水平冲量，使小球始终不离开圆形轨道在竖直圆内运动，试求冲量应满足的条件？