5．答案：

说明：本题是由课本例题改编的．关键是要把空间问题转化为平面问题．

基础训练5变式：

4．答案：

3．答案：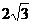　 　　

点评：三视图识别的过程是学生根据视图进行想象，在大脑中构建一个立体形象的过程,对空间想象能力要求较高，思维难度较大，应让学生紧紧抓住三个视图 在量上的关系“长对正，高平齐，宽相等”特征。

2．答案：由三视图知该几何体是底面为正方形的长方体，显然①可能，②不可能，③④⑤如右图知都有可能。

点评：将几何体的概念与三视图结合起来考查较为灵活。

1．答案：①④

点评：考查三棱锥概念的认识。由此复习回顾各种几何体的概念。

设计意图：考查柱、锥、台、球及其简单组合体的识图问题

5、(江苏省南通市2008届高三第二次调研考试)有一根长为6cm，底面半径为0.5cm的圆柱型铁管，用一段铁丝在铁管上缠绕4圈，并使铁丝的两个端点落在圆柱的同一母线的两端，则铁丝的长度最少为　 　　　cm．

二　感悟解答

4、(江苏省南京市2008届高三第一次调研测试)如图，已知一个多面体的平面展开图由一边长为1的正方体和4个边长为1的正三角形组成，则该多面体的体积是　 　▲　　 ．

3、(广东省佛山市2008年高三教学质量检测一)如图,水平放置的三棱柱的侧棱长和底边长均为2，且侧棱,正视图是边长为2的正方形，

该三棱柱的左视图面积为(　 ).

考点2、柱、锥、台、球的表面积和体积

2、(广东省揭阳市2008年高中毕业班高考调研测试)已知一几何体的三视图如下，正视图和侧视图都是矩形，俯视图为正方形，在该几何体上任意选择4个顶点，它们可能是如下各种几何形体的4个顶点，这些几何形体是　　　　　　　　 (写出所有正确结论的编号)．

①矩形；

②不是矩形的平行四边形；

③有三个面为直角三角形，有一个面为等腰三角形的四面体；

④每个面都是等腰三角形的四面体；

⑤每个面都是直角三角形的四面体．

1、(湖北省黄冈市麻城博达学校2008届三月综合测试)下面是关于三棱锥的四个命题：

①底面是等边三角形，侧面与底面所成的二面角都相等的三棱锥是正三棱锥；

②底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；

③底面是等边三角形，侧面的面积都相等的三棱锥是正三棱锥；

④侧棱与底面所成的角都相等，且侧面与底面所成的二面角都相等的三棱锥是正三锥．

其中真命题的编号是_____________