[例1]一直线与直二面角的两个面所成的角分别为α，β，则α+β满足(　　 ).

A.α+β<90⁰　　 B.α+β≤90⁰　 C.α+β>90⁰　 D.α+β≥90⁰

错解:A.

错因：忽视直线与二面角棱垂直的情况.

正解：B.

[例2].如图，△ABC是简易遮阳棚，A，B是南北方向上两个定点，正东方向射出的太阳光线与地面成40°角，为了使遮阴影面ABD面积最大，遮阳棚ABC与地面所成的角应为(　 ).

A．90°　　　 　B．60°　 　 　C．50°　　　 　D．45°

错解:A.

正解：C

[例3]已知正三棱柱ABC-A₁B₁C₁底面边长是10，高是12，过底面一边AB，作与底面ABC成角的截面面积是_____.

错解：.用面积射影公式求解：S_底=S截=.

错因：没有弄清截面的形状不是三角形而是等腰梯形.

正解：.

[例4]点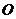是边长为4的正方形的中心，点，分别是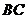，的中点．沿对角线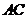把正方形折成直二面角D－AC－B．

(1)求的大小；

(2)求二面角的大小．

错解:不能认识折叠后变量与不变量.不会找二面角的平面角.

正解：(1)如图，过点E作EG⊥AC，垂足为G，过点F作FH⊥AC，垂足为H，则，．

因为二面角D－AC－B为直二面角，

又在中，，

．

．　

(2)过点G作GM垂直于FO的延长线于点M，连EM．

∵二面角D－AC－B为直二面角，∴平面DAC⊥平面BAC，交线为AC，又∵EG⊥AC，∴EG⊥平面BAC．∵GM⊥OF，由三垂线定理，得EM⊥OF．

∴就是二面角的平面角．

在RtEGM中，，，，

∴．∴．

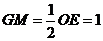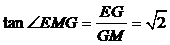所以，二面角的大小为

[例5]如图，平面α∥平面β∥平面γ，且β在α、γ之间，若α和β的距离是5，β和γ的距离是3，直线和α、β、γ分别交于A、B、C，AC＝12，则AB＝　　　 ，BC＝　　　　 .

解:作′⊥α，

∵　α∥β∥γ，∴　′与β、γ也垂直，

′与α、β、γ分别交于A₁、B₁、C₁.

因此，A₁B₁是α与β平面间的距离，B₁C₁是β与γ平 面间的距离，A₁C₁是α与γ之间的距离.　

∴　A₁B₁＝5，B₁C₁＝3，A₁C₁＝8，又知AC＝12

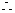AB= ， ，BC= .

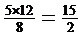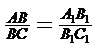答：AB= ，BC＝ .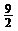

[例6] 如图，线段PQ分别交两个平行平面α、β于A、B两点，线段PD分别交α、β于C、D两点，线段QF分别交α、β于F、E两点，若PA＝9，AB＝12，BQ＝12，△ACF的面积为72，求△BDE的面积.

解：∵平面QAF∩α＝AF，平面QAF∩β＝BE

又∵α∥β，∴　AF∥BE

同理可证：AC∥BD.∴∠FAC与∠EBD相等成互补

由FA∥BE，得：BE：AF＝QB：QA＝12：24＝1：2，∴BE=　

由BD∥AC，得：AC：BD＝PA：PB＝9：21＝3：7，∴BD=　

又∵△ACF的面积为72，即 ＝72

S=

=,

答：△BDE的面积为84平方单位.

[例7]如图，B为ACD所在平面外一点，M、N、G分别为ABC、ABD、BCD的重心.

(1)求证：平面MNG∥平面ACD

(2)求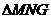S：S

解:(1)连结BM、BN、BG并延长交AC、AD、CD分别于P、F、H

∵　M、N、G分别为△ABC、△ABD、△BCD的重心，

则有：

连结PF、FH、PH有MN∥PF

又PF 平面ACD

∴　MN∥平面ACD

同理：MG∥平面ACD，MG∩MN＝M

∴　平面MNG∥平面ACD.

(2)由(1)可知：

∴MG=，又PH=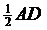

∴MG=　 ，

同理：NG= ，

∴　△MNG∽△ACD，其相似比为1：3

∴S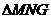：S₌　1：9

[例8]如图，平面EFGH分别平行于CD、AB，E、F、G、H分别在BD、BC、AC、AD上，且CD＝a，AB＝b，CD⊥AB.

(1)求证：EFGH是矩形.

(2)求当点E在什么位置时，EFGH的面积最大.

(1)证明：∵CD∥面EFGH,而面EFGH∩面BCD＝EF.∴CD∥EF

同理HG∥CD.∴EF∥HG

同理HE∥GF.∴四边形EFGH为平行四边形

由CD∥EF，HE∥AB

∴∠HEF为CD和AB所成的角或其补角，

又∵CD⊥AB.∴HE⊥EF.∴四边形EFGH为矩形.

(2)解：由(1)可知在△BCD中EF∥CD，其中DE＝m，EB＝n

∴

由HE∥AB

∴

又∵四边形EFGH为矩形

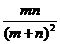∴S_矩形EFGH＝HE·EF＝·b·a＝ab

∵m+n≥2，∴(m+n)²≥4mn

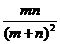∴≤，当且仅当m＝n时取等号，即E为BD的中点时,

S_矩形EFGH=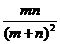ab≤ab，

　　 矩形EFGH的面积最大为ab.

点评：求最值时经常转化为函数求最值、不等式求最值、导数求最值、线性规划求最值等.

5．注意二面角的范围是，找二面角的平面角时要注意与棱的垂直直线，这往往是二面角的平面角的关键所在.求二面角的大小还有公式,用的时候要进行交代.在二面角棱没有给出的情况下求二面角大小方法一：补充棱；方法二：利用“如果”；方法三：公式等，求二面角中解三角形时注意垂直(直角)、数据在不同的面上转换.

4.在证明垂直时注意线线垂直、线面垂直及面面垂直的判定定理和性质定理的反复运用.

3．对于命题“三个平面两两相交，有三条交线，则这三条交线互相平行或者相交于同一点.”要会证明.

2．面面平行也是推导线面平行的重要手段；还要注意平行与垂直的相互联系，如：如果两个平面都垂直于同一条直线，则这两个平面平行；如果两条直线都垂直于一个平面，则这两条直线平行等.在证明平行时注意线线平行、线面平行及面面平行的判定定理和性质定理的反复运用.

1．两个平面的位置关系关系的判定关键看有没有公共点.

4．二面角的有关概念(从一条直线出发的两个半平面所组成的图形叫做二面角)与运算； 二面角的平面角(以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角)，二面角的平面角的常见作法(定义法、三垂线定理及逆定理法、垂面法等).

3．理解并掌握空间两个平面垂直的定义(一般地，两个平面相交，如果它们所成的二面角是直二面角,就说这两个平面垂直)；判定定理(如果一个平面经过另一个平面的一条垂线，那么这两个平面垂直)和性质定理(如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面).

2．理解并掌握空间两个平面平行的定义；掌握空间两个平面平行判定定理(如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行)和性质定理(如果两个平行平面同时和第三个平面相交，那么它们的交线平行).

1．空间两个平面的位置关系(有交点的是相交；没交点的是平行).