4．从七边形的某个顶点出发，分别连接这个顶点与其余各顶点，可以把七边形分成_____个三角形．

3.下列平面图中不能围成立方体的是(　).

2．直角三角形绕它最长边(即斜边)旋转一周得到的几何体为(　)

1．一个直立在水平面上圆柱体的主视图、俯视图、左视图分为(　)

A．长方形、圆、矩形　　　　　　 B．矩形、长方形、圆

C．圆、长方形、矩形　　　　　　 D．长方形、矩形、圆

[例1]如图，该物体的俯视图是(　).

错解：B.

错因：投影方向不对.

正解：C.

[例2] 如图所示的正方体中，E、F分别是AA₁,D₁C₁的中点，G是正方形BDB₁D₁的中心，则空间四边形AGEF在该正方体面上的投影不可能是( )

A　　　　　　　　 B　　　　　　　 C　　　　　　　 D

错解：C.

正解：D

　[例3]水平放置的△ABC有一边在水平线上，它的直观图是正△A₁B₁C₁，则△ABC是(　 )

A. 锐角三角形　B. 直角三角形　　C. 钝角三角形　 　D. 任意三角形

错解：B.

错因：不熟悉斜二侧画法的规则.

正解:C.

[例4] 正方体的全面积是a²，它的顶点都在球面上，这个球的表面积是(　 ).

A. 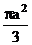　　　　 B. 　　　　 C. 　　　　　　 D.

错解：A.

错因：对正方体和球的关系理解不清.

正解:B.正方体的对角线就是球的直径.

[例5](06年江西卷)如图，在四面体ABCD中，截面AEF经过四面体的内切球(与四个面都相切的球)球心O，且与BC，DC分别截于E、F，如果截面将四面体分成体积相等的两部分，设四棱锥A－BEFD与三棱锥A－EFC的表面积分别是S₁，S₂，则必有(　 )

A.S₁<S₂B.S₁>S₂C.S₁=S₂D.S₁，S₂的大小关系不能确定

解：连OA、OB、OC、OD

则V_A－BEFD＝V_O－ABD+V_O－ABE+V_O－BEFD

V_A－EFC＝V_O－ADC+V_O－AEC+V_O－EFC又V_A－BEFD＝V_A－EFC而每个三棱锥的高都是原四面体的内切球的半径，故S_ABD+S_ABE+S_BEFD＝S_ADC+S_AEC+S_EFC又面AEF公共，故选C

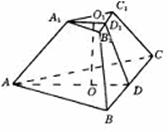[例6]正三棱台A₁B₁C_1-ABC的侧面与底面成45°角，求侧棱与底面所成角的正切值.

解：解法一　如图，设O₁，O为上下底面正三角形的中心，连接O₁O，A₁O₁交A₁B₁于D₁，AO交AB于D.连接D₁D.易证A₁O₁⊥B₁C₁，AD⊥BC，D₁D⊥BC，过A₁，D₁分别作A₁E⊥底面ABC，D₁F⊥底面ABC，易证E、F在AD上.

因为正三棱台A₁B₁C_1-ABC的侧面与底面成45°的二面角，所以∠D₁DA=45°.因此A₁E=O₁O=D₁F=FD.设该正三棱台上下底面的边长为a,b,则AD=b,A₁D₁=a.

所以　 A₁E=O₁O=D₁F=FD=b-= (b-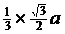a).

AE=(b-a).

所以　 tan∠A₁AE=.

解法二　如图，延长AA₁，BB₁，CC₁，则AA₁，BB₁，CC₁相交于一点S.显然点S在DD₁的延长线上.由解法一得知，∠SDA为二面角S-BC-A的平面角，故∠SDA=45°.

所以　 在RtΔSOD中，SO=OD，

因为　 AO=2·OD，所以　 tan∠SAO=.

点评:由此例可以看出，在解决棱台的问题时，“还台为锥”利用棱锥的性质来解决棱台问题是一种快捷方便的方法.

[例7] 粉碎机的下料斗是正四棱台形，如图所示，它的两底面边长分别是80 mm和440 mm，高是200 mm，计算：

(1)这个下料斗的体积；

(2)制造这样一个下料斗所需铁板的面积(保留两个有效数字)？

分析：要求下料斗所需铁板的面积，就是求正四棱台的侧面积.正四棱台的侧面积公式是S_侧＝(c+c＇)h＇.

解：(1)因为S_上＝440²mm²，S_下＝80² mm²，h＝200 mm

(2)下底面周长c＇＝4×80＝320mm，

　　　 下底面周长c＝4×440＝1760mm，

　　　 斜高h＇＝

　　　 S_正棱台侧＝(c+c＇)h＇＝(1760+320)×269≈2.8×10⁵(mm²)

答：这个下料斗的体积约为1.6×10⁷mm³，制造这样一个下料斗需铁板约2.8×10⁵mm².

点评：对于实际问题，须分清是求几何体的表面积，还是求侧面积，还是求侧面积与一个底面面积的和，还是求体积.

2．主视图的上、下、左、右对应物体的上、下、左、右；俯视图的上、下、左、右对应物体的后、前、左、右；左视图的上、下、左、右对应物体的上、下、后、前.

1．三视图间基本投影关系的三条规律：主视图与俯视图长对正，主视图与左视图高平齐，俯视图与左视图宽相等.概括为“长对正，高平齐，宽相等”；看不见的画虚线.

3.　　 注意投影和射影的关系，以及在解题中的作用.

2.　　 了解三视图的有关概念(视图是指将物体按正投影向投影面投　射所得到的图形.光线自物体的前面向后面投射所得的投影称之为主视图或正视图，自上而下的称为俯视图，自左向右的称为左视图，用这三种视图刻画空间物体的结构，称之为三视图);了解三视图画法规则，能作出物体的三视图.

1.　　 了解投影(投影线通过物体，向选定的面透射，并在该面上得到图形的方法)、中心投影(投射线交于一点的投影称为中心投影)、平行投影(投影线互相平行的投影称为平行投影)、斜投影(平行投影投射方向不是正对着投影面的投影)、正投影(平行投影投射方向正对着投影面的投影)的概念.