
1.直线与圆的位置关系的判定方法.
(1)方法一 直线: ;圆:
;圆: .
.

 一元二次方程
一元二次方程

(2)方法二 直线:  ;圆:
;圆: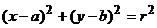 ,圆心(
,圆心( ,b)到直线的距离为
,b)到直线的距离为
d=


8.确定圆方程需要有三个互相独立的条件。圆的方程有两种形式,要知道两种形式之间的相互转化及相互联系
(1)圆的标准方程: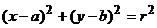 ,其中(
,其中( ,b)是圆心坐标,
,b)是圆心坐标, 是圆的半径;
是圆的半径;
(2)圆的一般方程: (
( >0),圆心坐标为(-
>0),圆心坐标为(- ,-
,- ),半径为
),半径为 =
= .
.
7.点到直线的距离公式.
(1)已知一点P( )及一条直线
)及一条直线 :
: ,则点P到直线
,则点P到直线 的距离d=
的距离d=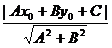 ;
;
(2)两平行直线 1:
1:  ,
,  2:
2:  之间的距离d=
之间的距离d= .
.
6.怎么判断两直线是否平行或垂直?判断两直线是否平行或垂直时,若两直线的斜率都存在,可以用斜率的关系来判断;若直线的斜率不存在,则必须用一般式的平行垂直条件来判断.
(1)斜率存在且不重合的两条直线 1∶
1∶ ,
,  2∶
2∶ ,有以下结论:
,有以下结论:
① 1∥
1∥ 2
2
 =
= ,且b1=b2
,且b1=b2
② 1⊥
1⊥ 2
2
 ·
· = -1
= -1
(2)对于直线 1∶
1∶ ,
, 2 ∶
2 ∶ ,当
,当 1,
1, 2,
2, 1,
1, 2都不为零时,有以下结论:
2都不为零时,有以下结论:
① 1∥
1∥ 2
2
 =
= ≠
≠
② 1⊥
1⊥ 2
2
 1
1 2+
2+ 1
1 2 = 0
2 = 0
③ 1与
1与 2相交
2相交
 ≠
≠
④ 1与
1与 2重合
2重合
 =
= =
=
5.两条直线的夹角。当两直线的斜率 ,
, 都存在且
都存在且 ·
· ≠ -1时,tanθ=
≠ -1时,tanθ= ,当直线的斜率不存在时,可结合图形判断.另外还应注意到:“到角”公式与“夹角”公式的区别.
,当直线的斜率不存在时,可结合图形判断.另外还应注意到:“到角”公式与“夹角”公式的区别.
4.确定直线方程需要有两个互相独立的条件。直线方程的形式很多,但必须注意各种形式的直线方程的适用范围.
|
名称 |
方程 |
说明 |
适用条件 |
|
斜截式 |
 |
 为直线的斜率 为直线的斜率b为直线的纵截距 |
倾斜角为90°的直线不能用此式 |
|
点斜式 |
 |
( ) 为直线上的已知点, ) 为直线上的已知点, 为直线的斜率 为直线的斜率 |
倾斜角为90°的直线不能用此式 |
|
两点式 |
 = = |
( ),( ),( )是直线上两个已知点 )是直线上两个已知点 |
与两坐标轴平行的直线不能用此式 |
|
截距式 |
 + + =1 =1 |
 为直线的横截距 为直线的横截距b为直线的纵截距 |
过(0,0)及与两坐标轴平行的直线不能用此式 |
|
一般式 |
 |
 , , , , 分别为斜率、横截距和纵截距 分别为斜率、横截距和纵截距 |
A、B不全为零 |
3.直线的倾斜角和斜率的关系
(1)每一条直线都有倾斜角,但不一定有斜率.
(2)斜率存在的直线,其斜率 与倾斜角α之间的关系是
与倾斜角α之间的关系是 =tanα.
=tanα.
2.定比分点公式:定比分点公式是解决共线三点A(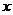 1,
1, 1),B(
1),B(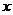 2,
2, 2),P(
2),P(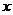 ,
, )之间数量关系的一个公式,其中λ的值是起点到分点与分点到终点的有向线段的数量之比.这里起点、分点、终点的位置是可以任意选择的,一旦选定后λ的值也就随之确定了.若以A为起点,B为终点,P为分点,则定比分点公式是
)之间数量关系的一个公式,其中λ的值是起点到分点与分点到终点的有向线段的数量之比.这里起点、分点、终点的位置是可以任意选择的,一旦选定后λ的值也就随之确定了.若以A为起点,B为终点,P为分点,则定比分点公式是 .当P点为AB的中点时,λ=1,此时中点坐标公式是
.当P点为AB的中点时,λ=1,此时中点坐标公式是 .
.
1.两点间的距离公式:不论A(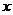 1,
1, 1),B(
1),B(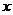 2,
2, 2)在坐标平面上什么位置,都有d=|AB|=
2)在坐标平面上什么位置,都有d=|AB|= ,特别地,与坐标轴平行的线段的长|AB|=|
,特别地,与坐标轴平行的线段的长|AB|=|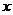 2-
2-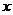 1|或|AB|=|
1|或|AB|=| 2-
2- 1|.
1|.
5. 在球心同侧有相距9cm的两个平行截面,它们的面积分别为49πcm2和400πcm2,求球的表面积.
第七章 平面解析几何初步
§7.1直线和圆的方程
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com