1、已知函数f(x)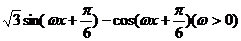＝图象的两相邻对称轴间的距离为。

(1)求f(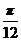)的值；(2)将函数y＝f(x)的图象向右平移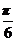个单位后，得到函数y＝g(x)的图象，求g(x)的最大值及相应的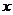的集合。

解答：由题得，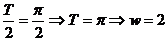

所以f(x)＝，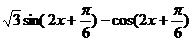

=

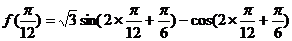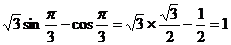
f(x)＝=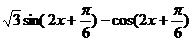

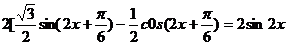
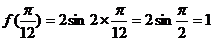
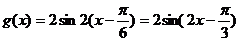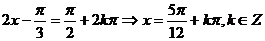，当时，

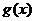有最大值2，此时

命题意图：此题是由08年高考题改编的,综合考查三角函数的求值、三角恒等变换、图象和性质。

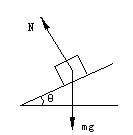
　 例1．物体在倾角为θ的斜面上滑动，则在下列两种情况下，物体加速度为多大？

(1)斜面是光滑的；

(2)斜面是粗糙的，且与物体间动摩擦因数为μ　　　　

分析：两种情况的主要差别就在于“是否受到动摩擦力的作用”

解：(1)对于光滑斜面，无论物体沿斜面向下滑或是沿斜面向上滑，其受力情况均可由图2所示，建立适当的坐标系后便可列出运动方程

　　　　　　　　 mgsinθ=ma₁，

得　　　　　　　 a₁=gsinθ.

(2)对于粗糙斜面，物体滑动时还将受动摩擦力作用，只是物体向下滑时动摩擦力方向沿斜面斜向上；物体向上滑时动摩擦力方向沿斜面斜向下，受力图分别如图3中(a)、(b)所示，建立适当的坐标系后便可分别列出方程组

　

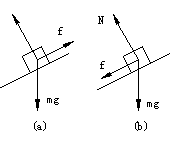
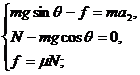
和

　

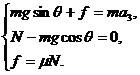
由此便可分别解得　　　　　　　　　　　　　

　　　　 a₂=g(sinθ－μcosθ)，　　　　　　　　 图3

　　　　 a₃=g(sinθ+μcosθ).

　例2．如图8-4所示，质量分别为15kg和5kg的长方形物体A和B静止叠放在水平桌面上.A与桌面以及A、B间动摩擦因数分别为μ₁=0.1和μ₂=0.6，设最大静摩擦力等于滑动摩擦力。问：

(1)水平作用力F作用在B上至少多大时，A、B之间能发生相对滑动？

(2)当F=30N或40N时，A、B加速度分别各为多少？

　

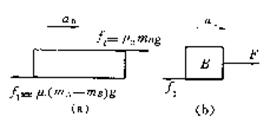
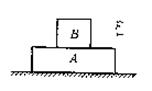
　　　　　　 图4　　　　　　　　　　　　　　　 图5

分析：AB相对滑动的条件是：A、B之间的摩擦力达到最大静摩擦力，且加速度达到A可能的最大加速度a₀，所以应先求出a₀.

解：(1)以A为对象，它在水平方向受力如图8-5(a)所示，所以有

　　　 m_Aa₀=μ₂m_Bg－μ₁(m_A+m_B)g，

a₀=g=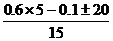×10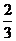m/s²=m/s²

再以B为对象，它在水平方向受力如图8-5(b)所示，加速度也为a₀，所以有

　　　　　 F－F₂=m_Ba₀，

F=f₂+m_Ba₀=0.6×5×10N+5×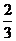N=33.3N.

即当F达到33.3N时，A、B间已达到最大静摩擦力.若F再增加，B加速度增大而A的加速度已无法增大，即发生相对滑动，因此，F至少应大于33.3N.

(2)当F=30N，据上面分析可知不会发生相对滑动，故可用整体法求出共同加速度

　a_A=a_B=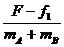=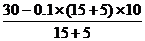m/s²=0.5m/s².

还可以进一步求得A、B间的静摩擦力为27.5N(同学们不妨一试).

当F= 40N时，A、B相对滑动，所以必须用隔离法分别求a_A、a_B，其实a_A不必另求，

　　　　　　 a_A=a₀=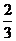m/s².

以B为对象可求得

　　　　 a_B=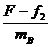=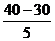m/s²=2m/s².

从上可看出，解决这类问题关键是找到情况发生变化的“临界条件”.各种问题临界条件不同，必须对具体问题进行具体分析。

例3．如图6(a)所示，质量为M的滑块与倾角为θ的斜面间的动摩擦因数为μ.滑动上安装一支架，在支架的O点处，用细线悬挂一质量为m的小球.当滑块匀加速下滑时，小球与滑块相对静止，则细线的方向将如何？

　

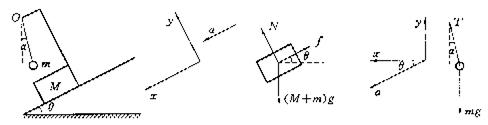
　　　 (a)　　　　　　　　　　　 (b)　　　　　　　　　　 (c)

　　　　　　　　　　　　　　　　 图6

分析：要求细线的方向，就是要求细线拉力的方向，所以这还是一个求力的问题.可以用牛顿第二定律先以整体以求加速度a(因a相同)，再用隔离法求拉力(方向).

解：以整体为研究对象，受力情况发图8-6(b)所示，根据牛顿第二定律有

　　 (M+m)gsinθ－f=(M+m)a，N－(M+m)gcosθ=0.

而f=μN，故可解得 a=g(sinθ－μcosθ).

　 再以球为研究对象，受务情况如图8-6(c)表示，取x、y轴分别为水平、竖直方向(注意这里与前面不同，主要是为了求a方便).由于加速度a与x轴间的夹角为θ，根据牛顿第二定律有

　　　　　　　　 Tsinα=macosθ，mg－Tcosα=masinθ.

　 由此得

tanα==.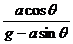

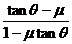　 为了对此解有个直观的认识，不妨以几个特殊μ值代入

　　 (1)μ=0，α=θ，绳子正好与斜面垂直；

(2)μ=tanθ，α=0⁰，此时物体匀速下滑，加速度为0，绳子自然下垂；

(3)μ＜tanθ，则α＜θ，物体加速下滑.

例4．如图7所示，质量M=10kg的斜面体，其斜

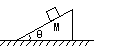面倾角θ=37⁰，小物体质量m=1kg，当小物体由静止释放

时，滑下S=1.4m后获得速度σ=1.4m/s，这过程斜面体处

于静止状态，求水平面对斜面体的支持力和静摩擦力(取

g=10m/s²)

分析：若采用隔离法求解，小物体与斜面体受力情　　　　　

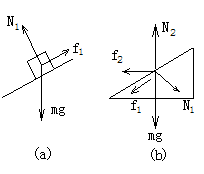况如图8(a)与(b)所示，由此根据运动学规律，

牛顿定律及平衡方程依次得

　 2as=υ²

　 mgs=θ－f₁=ma

　 N₁－mgcosθ=0

　F₂+f₁cosθ－Ns=θ=0

　　　　　 N₂－f₁s=θ－N₁cosθ－Mg=0

由此可求得水平面对斜面体的支持力N₂和静摩擦

力f₂的大小分别为

　　　　　 N₂=109.58N

　　　　　 f₂=0.56N　　　　　　　　　　　　　　　　　　　　

但若采用整体法，通知牛顿运动定律的修正形式，可给出如下简单的解合。

　 解：由运动学公式得

　　　　 2as=υ²

再由牛顿运动定律的修正形式得

　　　　　 f₂=macosθ

　　　　 mg+Mg－N₂=masinθ

于是解得

　　　　　　　 N₂=109.58N

　　　　　　　 f₂=0.56N

例5．如图9所示，升降机地板上有一木桶，桶内水面上漂浮着一个木块，当升降机静止时，木块有一半浸在水中，若升降机以a=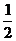g的加速度匀加速上升时，木块浸入水中的部分占总体积的__________。

分析：通常会有同学作出如下分析。

当升降机静止时，木块所受浮力F₁与重力平衡，于是

　　　 F₁－mg=0

　　　 F₁=ρ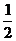Vg

当升降机加速上升时，木块所受浮力F₂比重大，此时有

　　　 F₂－mg=ma=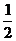mg

　　　 　F₂=ρV^/g

在此基础上可解得

　　 V^/ ：V=3 ：4

但上述结论是错误的，正确解答如下。

　解：当升降机静止时有

　　 F₁－mg=0

　　 F₁=ρ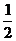Vg

当升降机加速上升时，系统处于超重状态，一方面所受浮力F₂确实大于木块的重力mg，有

　　　　　　 F₂－mg=ma=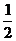mg

另一方面所排开的体积为V^/的水的视重大于其真重ρV^/g，而等于

　　　　　　 F₂=G_排=ρV^/(g+a)=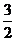ρV^/g

由此解得

　　 V^/ ：V=1 ：2

即：浸入水中的部分仍占木块体积的一半。

5．超重与失重

　 (1)真重与视重。

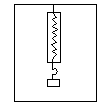如图1所示，在某一系统中(如升降机中)用

弹簧秤测某一物体的重力,悬于弹簧秤挂钩下的物体静

止时受到两个力的作用：地球给物体的竖直向上的重

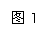力mg和弹簧秤挂钩给物体的竖直向上的弹力F，这

里，mg是物体实际受到的重力，称力物体的真重；

F是弹簧秤给物体的弹力，其大小将表现在弹簧秤的　　　　　　

示数上，称为物体的视重。

　 (2)起重与失重

　 通常情况下测物体的重力时，视重等于真重，我们就以弹簧秤的示数作为物体重力大小的测量值。当系统(升降机)做变速运动时，有时会使得视重大于真重，此时称为超重现象；有时会使得视重大小真重，此时称为失重现象；甚至有时会做视重等于零，此时称为完全为重现象。

　 (3)超重与失重的条件

　 由牛顿第二定律不难判断：当图8-1中的升降机做变速运动，有竖直向上的加速度a时，可由

F－mg=ma

　 得

　　　　　　　 　F=m(g+a)＞mg

在此条件下，系统处于超重状态；当图8-1中的升降机做变速运动，有竖直向上的加速度a时，可由

mg－F=ma

　得

F=m(g－a)＜mg

在此条件下，系统处于失重状态；当图8-1中的升降机做变速运动，有竖直向下的加速度a且

a=g

时，视重将为

F=0

在此条件下，系统处于完全失重状态。

4．牛顿第二定律的修正形式

　 通常情况下，当把该定律应用于单一物体，或者是各个部分加速度完全相同的某系统时，定律的含义并不难理解：m为物体或系统的质量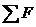，为物体或系统所受到的所有外力的矢量和，而a则为物体或系统的国速度。但若将定律直接应用于各个部分加速度并不完全相同的某系统时，一方面定律的表现形式要相应修正为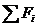=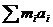；另一方面必须对定律的修正形式有一个正确的，同时也应该是更为深刻的理解：m_i为系统各部分的质量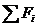，为系统各部分所受到的来自系统外部物体所施加的力的矢量和，而a_I则分别为系统各部分的不尽相同的加速度.

　 另外需要说明的是：尽管对于牛顿定律应用于加速度各不相同的系统时的修正形式，中学物理教学并未提出要求，但实际上我们确实会碰到大量的用“隔离法”(应用牛顿定律的原形)求解时非常复杂，而用“整体法”(应用牛顿定律的修正形式)则很简单的物理习题。

3．牛顿第二定律的基本应用步骤

　 (1)确定研究对象；

　 (2)分析受力情况与运动情况；

　 (3)建立适当的坐标系，将力与运动加速度作正交分解；

　 (4)沿各坐标轴方向列出动力学方程，进而求解.

2．对牛顿第二定律的理解

　 (1)内容：物体的加速度a与其合外力F成正比，与其质量m成反比.可表示为

F=ma.

　 (2)理解：F量化了迫使物体运动状态发生变化的外部作用，m量化了物体“不愿改变运动状态”的基本特性(惯性)，而a则描述了物体的运动状态(υ)变化的快慢。明确了上述三个量的物理意义，就不难理解如下的关系了：

a∝F，　 a∝.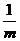

　 另外，牛顿第二定律给出的是F、m、a三者之间的瞬时关系，也是由力的作用效果的瞬时性特征所决定的。

1．对牛顿第一定律的理解

(1)内容：一切物体都将保持静止状态或匀速直线运动状态，直到有外力迫使其改变运动状态为止。

(2)理解：牛顿第一定律分别从物体的本质特征和相应的外部作用两个侧面对运动作出了深刻的剖析。就物体的本质特征而言，一切物体都具有“不愿改变其运动状态”的特性；就物体所受到的外力与其运动的关系而言，外力是迫使物体改变运动状态的原因。也就是说，牛顿第一定律一方面揭示出一切物体共同具备的本质特性--惯性，另一方面又指出了外力的作用效果之一--改变物体的运动状态。