
5. 设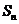 是数列
是数列 的前
的前 项和,对任意
项和,对任意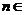 N
N 总有
总有 ,
,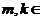 N
N 且
且 .
.
(Ⅰ)求数列 的通项公式
的通项公式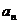 ;
;
(Ⅱ)试比较 与
与 的大小;
的大小;
(Ⅲ)当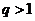 时,试比较
时,试比较 与
与 的大小.
的大小.
解:(Ⅰ)当 时,
时,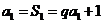 ,
,
 .
……1分
.
……1分

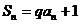 , ①
, ①
 .
②
.
②
②-①得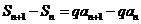 ,
,
 .
.
 .
……3分
.
……3分
 数列
数列 是首项为
是首项为 ,公比为
,公比为 的等比数列.
的等比数列.

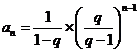 .
……4分
.
……4分
(Ⅱ)由(Ⅰ)得 . ……5分
. ……5分
令 , 则
, 则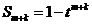 ,
, .
.
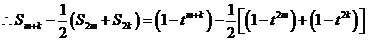 ……7分
……7分
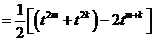
 .
.
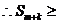
 .
……9分(Ⅲ)当
.
……9分(Ⅲ)当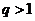 时,
时, ,
, 
 ,
,
 ,
,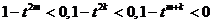 .
.
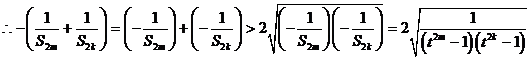 .
.
……11分
 0<
0<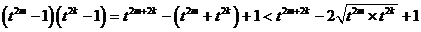
 .
.
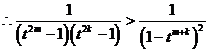 .
……13分
.
……13分
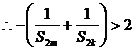
 .
.
 .
……14分
.
……14分
命题意图:本题主要考查数列的概念和不等式等知识,考查综合运用数学知识分析和解决问题能力.
4.在平面直角坐标系xOy巾,已知圆心在第二象限、半径为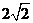 的圆C与直线
的圆C与直线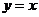 相切于坐标原点0.椭圆
相切于坐标原点0.椭圆 与圆c的一个交点到椭圆两焦点的距离之和为10.
与圆c的一个交点到椭圆两焦点的距离之和为10.
(1)求圆C的方程; (2)试探究圆C上是否存在异于原点的点Q,使Q到椭圆右焦点F的距离等于线段OF的长.若存在,请求出点Q的坐标;若不存在,请说明理由.
[解析](1)设圆的方程为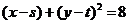 ………………………2分
………………………2分
依题意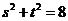 ,
,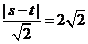 ,
,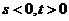 …………5分
…………5分
解得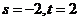 ,故所求圆的方程为
,故所求圆的方程为 ……………………7分
……………………7分
(注:此问若结合图形加以分析会大大降低运算量!)
(2)由椭圆的第一定义可得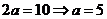 ,故椭圆方程为
,故椭圆方程为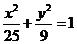 ,焦点
,焦点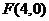 ……9分
……9分
设 ,依题意
,依题意 ,
, 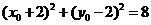 …………………11分
…………………11分
解得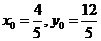 或
或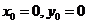 (舍去) ……………………13分 存在
(舍去) ……………………13分 存在 ……14分
……14分
命题意图:近几年的高考试题中常会出现存在性问题,让学生探究,提高学生的综合能力。
3.
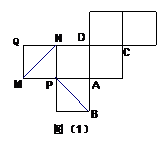 如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题。
如图(1)是一正方体的表面展开图,MN和PB是两条面对角线,请在图(2)的正方体中将MN和PB画出来,并就这个正方体解决下面问题。
(Ⅰ)求证:MN∥平面PBD;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求PB和平面NMB所成的角的大小.
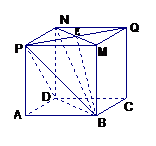
解:MN和PB的位置如右图示:(正确标出给1分)
(Ⅰ)∵ ND∥MB 且ND=MB
ND∥MB 且ND=MB
∴四边形NDBM为平行四边形
∴MN∥DB------------------------------------------3分
∵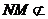 平面PDB,
平面PDB, 平面PDB
平面PDB
∴MN∥平面PBD--------------------------4分
(Ⅱ)∵ 平面ABCD,
平面ABCD,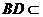 平面
平面 ,∴
,∴ -------------5分
-------------5分
又∵ ∴
∴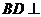 平面
平面 , ---------------------6分
, ---------------------6分
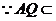 面
面 ∴
∴ ,同理可得
,同理可得 ,∵
,∵
∴ 面PDB
-------------------------------------8分
面PDB
-------------------------------------8分
(Ⅲ)连结PQ交MN于点E,
∵
 ,
,
∴ 平面
平面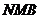
连结BE,则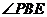 为PB和平面NMB所成的角---------12分
为PB和平面NMB所成的角---------12分
在直角三角形PEB中
∵ ∴
∴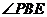 =30°
=30°
即PB和平面NMB所成的角为30°.--------------------------------------14分
命题意图:近几年文科考生对立体几何的考查要求降低了,但对传统证明方法的考查加强,对探究性问题更为重视。
2.已知a、b、c分别是△ABC中角A、B、C的对边,且 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若 ,求
,求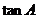 的值.
的值.
(Ⅰ)解:由余弦定理,得 =
= .
……2分
.
……2分
∵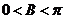 ,∴
,∴  .
……4分
.
……4分
(Ⅱ)解法一:将 代入
代入 ,得
,得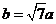 .
……6分
.
……6分
由余弦定理,得 .
……8分
.
……8分
∵ ,∴
,∴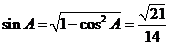 .
……10分
.
……10分
∴ .
……12分
.
……12分
解法二:将 代入
代入 ,得
,得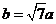 .
……6分
.
……6分
由正弦定理,得 . ……8分
. ……8分
∵ ,∴
,∴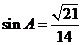 .
……10分
.
……10分
又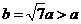 ,则
,则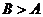 ,∴
,∴ .
.
∴ .
……12分
.
……12分
解法三:∵ ,
,
由正弦定理,得 .
……6分
.
……6分
∵ ,∴
,∴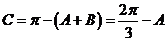 .
.
∴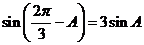 .
……8分
.
……8分
∴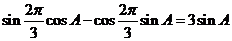 .
.
∴ .
.
∴ .
……10分
.
……10分
∴ .
……12分
.
……12分
考查意图:本小题主要考查正弦定理、余弦定理、同角三角函数的基本关系、解三角形等基础知识,考查运算求解能力
1.已知向量 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
解:  (2分)
(2分)
f´(x)=-3x2+2x+t, (3分)
若f(x)在(-1,1)上是增函数,则在(-1,1)上f´(x)≥0 (5分)
 的图象是开口向下的抛物线,
的图象是开口向下的抛物线,
∴当且仅当 即t≥5时满足条件
(10分)
即t≥5时满足条件
(10分)
所以若f(x)在(-1,1)上是增函数,则t的取值范围是[5,+∞)。 (12分)
命题意图:这道题主要涉及了向量、函数、二次函数等有关性质,是对学生基础知识的考查。
6、电信局为了配合客户不同需要,设有A、B两种方案这两种方案应付话费(元)与通话时间(分钟)之间的关系如图所示(MN//CD).
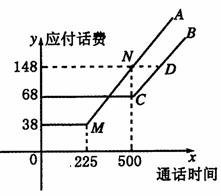 (1)若通话时间为250分钟,按方案A、B各付话费多少元?
(1)若通话时间为250分钟,按方案A、B各付话费多少元?
(2)方案B从500分钟以后,每分钟收费多少元?
(3)通话时间在什么范围内方案B才会比方案A优惠?
解:由图知M(225,38),C(500,68),N(500,148)


设这两种方案的应付话费与通话时间的函数关系式分别为 、
、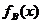 ,
,
则

(1)通话时间为250分钟时,方案A、B的费和分别为 (元),68元.
(元),68元.
(2)由直线CD的斜率的实际意义知方案B从500分钟以后每分钟收费0.4元.
(3)由图知:当
当 时,
时,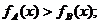 当
当 即
即
则
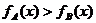 ,故当
,故当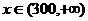 时,方案B较优惠。
时,方案B较优惠。
选题意图:本题是一道模拟原题,考查了学生读图解图能力,会由函数图象写出分段函数表达式,并用数学知识解决实际问题,是很好的一道题,若要修改,也可以是把其中一个图象换成抛物线。
5、如图,在直角梯形 中,
中, ,
, ,
, ,椭圆以
,椭圆以 、
、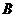 为焦点且经过点
为焦点且经过点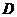 .(1)建立适当的直角坐标系,求椭圆E的方程;
.(1)建立适当的直角坐标系,求椭圆E的方程;
 (2)问是否存在过C点的直线
(2)问是否存在过C点的直线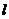 与椭圆E交于
与椭圆E交于 两点,且C为MN的中点,若存在,求出直线
两点,且C为MN的中点,若存在,求出直线  的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
解答:以AB所在直线为 轴,线段AB的中点O为坐标原点,建立直角坐标系,则
轴,线段AB的中点O为坐标原点,建立直角坐标系,则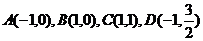 。
。
|
所以椭圆E的焦点为 即
即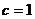 ,有椭圆E经过点D,
,有椭圆E经过点D,
所以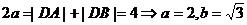 ,所以椭圆E的方程为
,所以椭圆E的方程为 。
。
(2)存在,设交点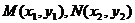 ,因为点C是MN的中点。所以
,因为点C是MN的中点。所以 ,且
,且 ,两式相减得
,两式相减得
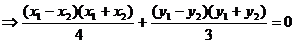
得出斜率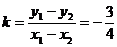 ,所以直线
,所以直线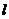 的方程为
的方程为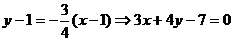
命题意图:本题是由一道模拟题,改变了第2问,考查了平面建系的思想,椭圆的定义,直线和圆锥曲线中点弦相关知识。
4、设M是由满足下列条件的函数 构成的集合:“①方程
构成的集合:“①方程
 有实数根;②函数
有实数根;②函数 在
在 上是单调递增;③直线
上是单调递增;③直线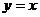 是函数
是函数 图象上的一条切线。”.试判断函数
图象上的一条切线。”.试判断函数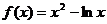 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;
解答:
 ,通过画两函数图象可知它们有交点,且交点的横坐标
,通过画两函数图象可知它们有交点,且交点的横坐标 。所以方程
。所以方程
 有实数根,
有实数根, 满足条件①;
满足条件①;
 令
令 。
。
所以 在
在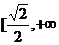 )上是增函数。故
)上是增函数。故 在
在 上是单调递增,
上是单调递增, 满足条件②;
满足条件②;
若直线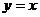 是函数
是函数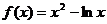 图象上的一条切线,则切线的斜率
图象上的一条切线,则切线的斜率 ,
,
设切点A( ),则有
),则有 解得
解得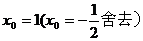 ,即
,即 ,
,
所以切点A(1,1),切线方程为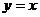 ,
, 满足条件③。所以函数
满足条件③。所以函数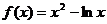 是集合M中的元素。
是集合M中的元素。
命题意图:本题是由一道模拟题改编,考查函数与方程、函数的图象、函数与导数及相关的性质。
3、如图,四棱锥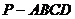 中,
中,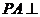 底面
底面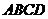 ,
,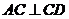 ,
,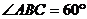 ,
,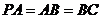 =2,CD=1,
=2,CD=1,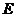 是
是 的中点.(1)求棱锥P-ABCD的体积;
的中点.(1)求棱锥P-ABCD的体积;
 (2)求证:
(2)求证: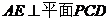 ;
;
解答: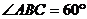 ,
,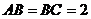

 是正三角形,AC=2
是正三角形,AC=2
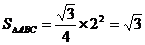
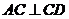


所以底面四边形ABCD的面积为
所以

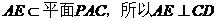 ,另
,另 ,即
,即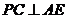 ,
,
由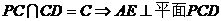 。
。
命题意图:考查四棱锥的体积运算,线线垂直、线面垂直等基础的几何知识。
2、等差数列 满足
满足 ,
,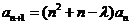 (
(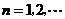 ),
), 是常数.
是常数.
(1)求出 和它的通项公式
和它的通项公式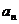 ;
;
(2)若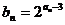 ,求证:
,求证: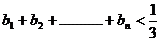 。
。
解答:当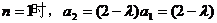 ,当
,当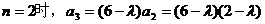
因为数列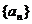 是等差数列,所以
是等差数列,所以
即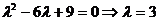 ,所以
,所以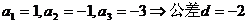 ,
,
所以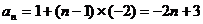 。
。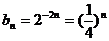 ,即数列{
,即数列{ 是等比数列,首项和公比都是
是等比数列,首项和公比都是 。所以
。所以 。
。
命题意图:本题也是一道高考修改题。考查等差数列、等比数列的重要元素、通项公式、求和公式及方程思想。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com