
4.双曲线 的左支上一点P,⊙O'为ΔPF1F2的内切圆,则圆心O'的横坐标为(B).
的左支上一点P,⊙O'为ΔPF1F2的内切圆,则圆心O'的横坐标为(B).
A、a B、-a C、 D、
D、
3. F1、F2为椭圆两个焦点,Q为椭圆上任一点,以任一焦点作∠F1QF2的外角平分线的垂线,垂足为P,则P点轨迹为(A).
A、圆 B、椭圆 C、双曲线 D、抛物线
2. 双曲线的虚轴长为4,离心率 ,F1、F2分别是它的左,右焦点,若过F1的直线与双曲线的左支交于A、B两点,且|AB|是|AF2|与|BF2|的等差中项,则|AB|为(A).
,F1、F2分别是它的左,右焦点,若过F1的直线与双曲线的左支交于A、B两点,且|AB|是|AF2|与|BF2|的等差中项,则|AB|为(A).
A、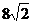 B、
B、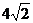 C、
C、 D、8
D、8
1. 若椭圆经过原点,且焦点为F1(1,0),F2(3,0),则其离心率为( C )
A.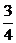 B.
B.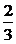 C.
C. D.
D.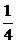
6.如图,F为双曲线C: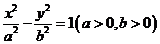 的右焦点。P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,
的右焦点。P为双曲线C右支上一点,且位于x轴上方,M为左准线上一点,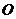 为坐标原点。已知四边形OFPM为平行四边形,|PF|=l|OF|。
为坐标原点。已知四边形OFPM为平行四边形,|PF|=l|OF|。
(Ⅰ)写出双曲线C的离心率e与l的关系式;
 (Ⅱ)当l=1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若|AB|=12,求此时的双曲线方程。
(Ⅱ)当l=1时,经过焦点F且平行于OP的直线交双曲线于A、B点,若|AB|=12,求此时的双曲线方程。
[专家解答]
∵四边形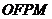 是€,∴
是€,∴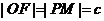 ,
,
作双曲线的右准线交PM于H,则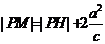 ,
,
又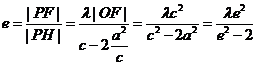 ,
,
 。
。
(Ⅱ)当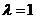 时,
时, ,
, ,
,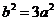 ,双曲线为
,双曲线为 四边形
四边形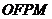 是菱形,所以直线OP的斜率为
是菱形,所以直线OP的斜率为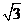 ,则直线AB的方程为
,则直线AB的方程为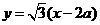 ,代入到双曲线方程得:
,代入到双曲线方程得: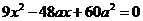 ,
,
又 ,由
,由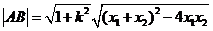 得:
得: ,解得
,解得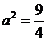 ,则
,则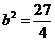 ,所以
,所以 为所求。
为所求。
★★★高考要考什么
[考点透视]
椭圆、双曲线、抛物线的定义,标准方程,简单的几何性质,椭圆的参数方程。
[热点透析]
主要题型:
(1)定义及简单几何性质的灵活运用;
(2)求曲线方程(含指定圆锥曲线方程及轨迹方程)。
题型一般为二小一大,小题基础灵活,解答题一般在中等难度以上,一般具有较高的区分度。
★★★突破重难点
[范例1]过椭圆左焦点F,倾斜角为60°的直线交椭圆于A、B两点,若|FA|=2|FB|,则椭圆的离心率为( B )
(A)  (B)
(B)  (C)
(C)
 (D)
(D)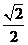
解:设点A、B到椭圆左准线的距离分别为d1,d2,|FA|=r1,|FB|=r2,
则 =e,即d1=
=e,即d1= ,同理d2=
,同理d2= ,两式相减得
,两式相减得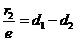 .
.
因为直线AB的倾斜角为60°, \ 2|d1-d2|=|AB|=3r2,e=
[点晴]本题的关键在于利用椭圆的第二定义将60°倾斜角、|FA|=2|FB|这两个条件与椭圆的离心率建立联系。
[文]若F1、F2为双曲线 的左、右焦点,O为坐标原点,点P在双曲线的左支上,点M在双曲线的右准线上,且满足:
的左、右焦点,O为坐标原点,点P在双曲线的左支上,点M在双曲线的右准线上,且满足:
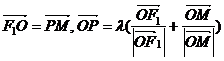
 ,
,
则该双曲线的离心率为( )
A. B.
B.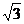 C.
C.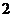 D.3
D.3
解:由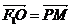 知四边形F1OMP是平行四边形,又
知四边形F1OMP是平行四边形,又
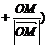
知OP平分∠F1OM,即F1OMP是菱形,设|OF1|=c,则|PF1|=c.
又|PF2|-|PF1|=2a, ∴|PF2|=2a+c,
由双曲线的第二定义知 ,且e>1,∴e=2,故选C.
,且e>1,∴e=2,故选C.
[范例2]定长为3的线段AB的两个端点在y=x2上移动,AB中点为M,求点M到x轴的最短距离。
分析:(1)可直接利用抛物线设点,如设A(x1,x12),B(x2,x22),又设AB中点为M(x0,y0)用弦长公式及中点公式得出y0关于x0的函数表达式,用函数思想求出最短距离。
(2)M到x轴的距离是一种“点线距离”,可先考虑M到准线的距离,想到用定义。
|
则
由①得(x1-x2)2[1+(x1+x2)2]=9, 即[(x1+x2)2-4x1x2]·[1+(x1+x2)2]=9 ④
由②、③得2x1x2=(2x0)2-2y0=4x02-2y0 代入④得[(2x0)2-(8x02-4y0)]·[1+(2x0)2]=9
∴ ,
,
 ≥
≥
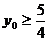
当4x02+1=3 即 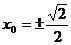 时,
时,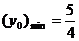 此时
此时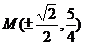
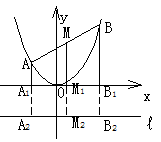 法2:如图
法2:如图
∴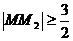 , 即
, 即 ,
,
∴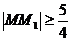 , 当AB经过焦点F时取得最小值。
, 当AB经过焦点F时取得最小值。
∴M到x轴的最短距离为
[点晴]解法一是列出方程组,利用整体消元思想消x1,x2,从而形成y0关于x0的函数,这是一种“设而不求”的方法。而解法二充分利用了抛物线的定义,巧妙地将中点M到x轴的距离转化为它到准线的距离,再利用梯形的中位线,转化为A、B到准线的距离和,结合定义与三角形中两边之和大于第三边(当三角形“压扁”时,两边之和等于第三边)的属性,简捷地求解出结果的,但此解法中有缺点,即没有验证AB是否能经过焦点F,而且点M的坐标也不能直接得出。请思考:当|AB|在什么范围内取值时不能用解法二?
[文](北京卷)椭圆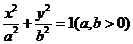 的两个焦点F1、F2,点P在椭圆C上,且PF1⊥PF2,| PF1|=
的两个焦点F1、F2,点P在椭圆C上,且PF1⊥PF2,| PF1|= ,| PF2|=
,| PF2|=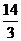 .
.
(I)求椭圆C的方程;
(II)若直线l过圆x2+y2+4x-2y=0的圆心M交椭圆于A、B两点,且A、B关于点M对称,求直线l的方程。
解法一:(Ⅰ)因为点P在椭圆C上,所以 ,a=3.
,a=3.
在Rt△PF1F2中,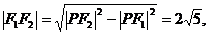 故椭圆的半焦距c=
故椭圆的半焦距c=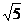 ,
,
从而b2=a2-c2=4, 所以椭圆C的方程为 =1.
=1.
(Ⅱ)设A,B的坐标分别为(x1,y1)、(x2,y2).
由圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1). 从而可设直线l的方程为y=k(x+2)+1, 代入椭圆C的方程得
(4+9k2)x2+(36k2+18k)x+36k2+36k-27=0.
因为A,B关于点M对称. 所以
解得 ,
,
所以直线l的方程为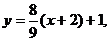 即8x-9y+25=0. (经检验,符合题意)
即8x-9y+25=0. (经检验,符合题意)
解法二:(Ⅰ)同解法一.
(Ⅱ)已知圆的方程为(x+2)2+(y-1)2=5,所以圆心M的坐标为(-2,1).
设A,B的坐标分别为(x1,y1),(x2,y2).由题意x1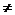 x2且
x2且
 ①
①
 ②
②
由①-②得  ③
③
因为A、B关于点M对称,所以x1+ x2=-4, y1+ y2=2,
代入③得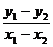 =
=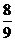 ,即直线l的斜率为
,即直线l的斜率为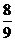 ,
,
所以直线l的方程为y-1=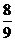 (x+2),即8x-9y+25=0.
(x+2),即8x-9y+25=0.
(经检验,所求直线方程符合题意.)
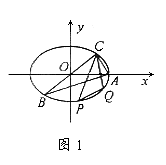 [范例3]如图1,已知A、B、C是长轴为4的椭圆上三点,点A是长轴的一个顶点,BC过椭圆中心O,且
[范例3]如图1,已知A、B、C是长轴为4的椭圆上三点,点A是长轴的一个顶点,BC过椭圆中心O,且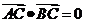 ,
,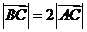 。
。
(1)建立适当的坐标系,求椭圆方程;
(2)如果椭圆上两点P、Q使直线CP、CQ与x轴围
成底边在x轴上的等腰三角形,是否总存在实数l
使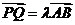 ?请给出证明。
?请给出证明。
解:(1)以O为原点,OA所在的直线为x轴建立如
图直角坐标系,则A(2,0),椭圆方程可设为
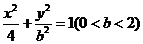 。
。
而O为椭圆中心,由对称性知|OC|=|OB|
又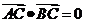 ,所以AC⊥BC
,所以AC⊥BC
又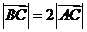 ,所以|OC|=|AC|,
,所以|OC|=|AC|,
所以△AOC为等腰直角三角形,所以点C坐标为(1,1)。将(1,1)代入椭圆方程得 ,则椭圆方程为
,则椭圆方程为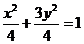 。
。
(2)由直线CP、CQ与x轴围成底边在x轴上的等腰三角形,设直线CP的斜率为k,则直线CQ的斜率为-k,直线CP的方程为y=k(x-1),直线CQ的方程为y=-k(x-1)。由椭圆方程与直线CP的方程联立,消去y得
(1+3k2)x2-6k(k-1)x+3k2-6k-1=0①
因为C(1,1)在椭圆上,所以x=1是方程①的一个根,于是
 同理
同理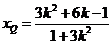
这样,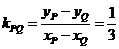 , 又B(-1,-1),所以
, 又B(-1,-1),所以 ,
,
即kAB=kPQ。所以PQ∥AB,存在实数l使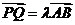 。
。
[点晴]利用斜率互为相反数关系,整体替换,可简化解题过程。
[文](06上海春)学校科技小组在计算机上模拟航天器变轨返回试验. 设计方案如图:航天器运行(按顺时针方向)的轨迹方程为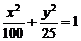 ,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以
,变轨(即航天器运行轨迹由椭圆变为抛物线)后返回的轨迹是以 轴为对称轴、
轴为对称轴、 为顶点的抛物线的实线部分,降落点为
为顶点的抛物线的实线部分,降落点为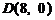 . 观测点
. 观测点 同时跟踪航天器.
同时跟踪航天器.
(1)求航天器变轨后的运行轨迹所在的曲线方程;
(2)试问:当航天器在 轴上方时,观测点
轴上方时,观测点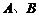 测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
测得离航天器的距离分别为多少时,应向航天器发出变轨指令?
解:(1)设曲线方程为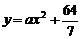 , 由题意可知,
, 由题意可知, .
.  .
.

 曲线方程为
曲线方程为 .
.
(2)设变轨点为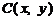 ,根据题意可知
,根据题意可知
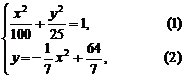
得  ,
,
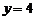 或
或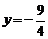 (不合题意,舍去).
(不合题意,舍去).
 .
.
得 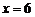 或
或 (不合题意,舍去).
(不合题意,舍去).
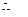
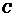 点的坐标为
点的坐标为 ,
, .
.
答:当观测点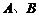 测得
测得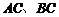 距离分别为
距离分别为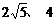 时,应向航天器发出指令.
时,应向航天器发出指令.
[范例4]过抛物线x2=4y上不同两点A、B分别作抛物线的切线相交于P点,

(1)求点P的轨迹方程;
(2)已知点F(0,1),是否存在实数l使得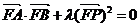 ?若存在,求出l的值,若不存在,请说明理由。
?若存在,求出l的值,若不存在,请说明理由。
解法(一):(1)设
由 得:
得:


直线PA的方程是 即
即 ①
①
同理,直线PB的方程是: ②
②
由①②得: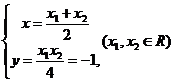 ∴点P的轨迹方程是
∴点P的轨迹方程是
(2)由(1)得:
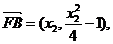

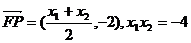 ,
,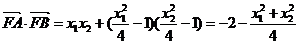
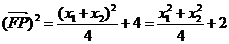 ,所以
,所以
故存在l=1使得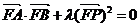
解法(二):(1)∵直线PA、PB与抛物线相切,且
∴直线PA、PB的斜率均存在且不为0,且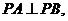
设PA的直线方程是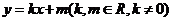
由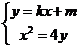 得:
得: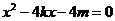
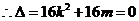 即
即
即直线PA的方程是: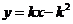
同理可得直线PB的方程是:
由 得:
得:
故点P的轨迹方程是
(2)由(1)得:
 ,
,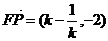
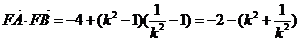
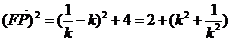
故存在l=1使得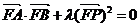
[点晴]抛物线的切线方程成了近几年高考试题中的一个考查亮点。解法一、解法二是解决抛物线切线问题的常用方法,应熟练掌握。
[文]已知△ABC的两顶点A、B分别是双曲线2x2-2y2=1的左、右焦点, 且sinC是sinA、sinB的等差中项.
(Ⅰ)求顶点C的轨迹T的方程;
(Ⅱ)设P(-2,0), 过点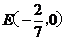 作直线l交轨迹T于M、N两点,问∠MPN的大小是否为定值?证明你的结论.
作直线l交轨迹T于M、N两点,问∠MPN的大小是否为定值?证明你的结论.
解:(Ⅰ) 由条件知A (-1 , 0 ) , B (1 , 0 ),且sinA + sinB = 2sinC
∴|BC| + |AC| = 2|AB| = 4
∴点C的轨迹是以A、B为焦点,长轴长2a = 4的椭圆(不包括x轴上两点).
∴点C的轨迹T的方程是 =1 (x≠±2)
=1 (x≠±2)
(Ⅱ) 当l⊥x轴时,直线l的方程为x =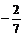 ,代入
,代入 =1解得M、N的坐标为(
=1解得M、N的坐标为( ),而|PE| =
),而|PE| = ,∴∠MPN = 90°,
,∴∠MPN = 90°,
猜测∠MPN= 90°为定值.
|
 证明:设直线l的方程为my = x +
证明:设直线l的方程为my = x +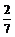 ,
,
由 ,得 (3m2 + 4) y2 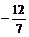 my
my = 0
= 0
∴y1 + y2
=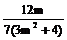 ,y1 y2 =
,y1 y2 =
∴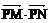 = (x1 + 2 , y1)·(x2 +2 , y2 ) = (x1 +
2 ) (x2 +2) + y1 y2
= (x1 + 2 , y1)·(x2 +2 , y2 ) = (x1 +
2 ) (x2 +2) + y1 y2
= (my1 + ) (my2 +
) (my2 + ) + y1 y2 = (m2
+1) y1 y2 +
) + y1 y2 = (m2
+1) y1 y2 + m (y1 + y2) +
m (y1 + y2) +
=(m2 +1)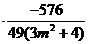 +
+ m
m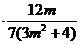 +
+ = 0
= 0
∴∠MPN = 90°,为定值.
★★★自我提升
5.已知椭圆中心在原点,一个焦点为F(-2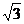 ,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是
,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 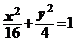 .
.
4.抛物线y=4x2上的一点M到焦点的距离为1,则点M的纵坐标是( B)
( A )  (
B )
(
B )  (
C )
(
C )  (
D ) 0
(
D ) 0
3.如果双曲线的两个焦点分别为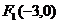 、
、 ,一条渐近线方程为
,一条渐近线方程为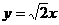 ,那么它的两条准线间的距离是( C
)
,那么它的两条准线间的距离是( C
)
A. B.
B. C.
C.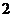 D.
D.
2.已知双曲线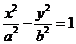 的一条渐近线方程为y=x,则双曲线的离心率为(A)
的一条渐近线方程为y=x,则双曲线的离心率为(A)
(A) (B) (C) (D)
1.已知△ABC的顶点B、C在椭圆 +y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是(C )
+y2=1上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是(C )
(A)2 (B)6 (C)4 (D)12
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com