
6. 如图,四面体ABCD中,O、E分别BD、BC的中点,
如图,四面体ABCD中,O、E分别BD、BC的中点,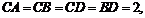

(Ⅰ)求证:AO⊥平面BCD;
(Ⅱ)求异面直线AB与CD所成角的大小;








(Ⅲ)求点E到平面ACD的距离.
[专家解答]
(I)证明:连结OC


在 中,由已知得
中,由已知得
而

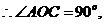 即
即

 平面
平面
(II)取AC的中点M,连结OM、ME、OE,由E为BC的中点知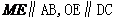
 直线OE与EM所成的锐角就是异面直线AB与CD所成的角
直线OE与EM所成的锐角就是异面直线AB与CD所成的角
在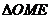 中,
中, 
 是直角
是直角 斜边AC上的中线,
斜边AC上的中线,
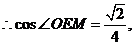
 异面直线AB与CD所成角的大小为
异面直线AB与CD所成角的大小为
(III)设点E到平面ACD的距离为


在 中,
中,

而

 点E到平面ACD的距离为
点E到平面ACD的距离为
★★★高考要考什么
[考点透视]
判断线线、线面、面面的平行与垂直,求点到平面的距离及多面体的体积。
[热点透析]
5.在正方形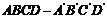 中,过对角线
中,过对角线 的一个平面交
的一个平面交 于E,交
于E,交 于F,则( )
于F,则( )
①
四边形 一定是平行四边形
一定是平行四边形
②
四边形 有可能是正方形
有可能是正方形
③
四边形 在底面ABCD内的投影一定是正方形
在底面ABCD内的投影一定是正方形
④
四边形 有可能垂直于平面
有可能垂直于平面
以上结论正确的为 ①③④ 。(写出所有正确结论的编号)
4.已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列
四个命题:①若 ; ②若
; ②若
③若 ;
;
④若m、n是异面直线, ,
,
其中真命题是( D)
A.①和② B.①和③ C.③和④ D.①和④
3.设三棱柱ABC-A1B1C1的体积为V,P、Q分别
是侧棱AA1、 CC1 上的点,且PA=QC1,则
四棱锥B-APQC的体积为( C )
A.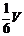 B.
B. C.
C. D.
D.
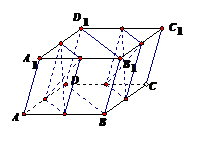
2.如图,过平行六面体ABCD-A1B1C1D1任意两条棱的中
点作直线,其中与平面DBB1D1平行的直线共有( D )
A.4条 B.6条 C.8条 D.12条
1.已知平面α外不共线的三点A,B,C到α的距离都相等,则正确的结论是( B)
 A.平面ABC必平行于α B. 存在△ABC的一条中位线平行于α或在α内
A.平面ABC必平行于α B. 存在△ABC的一条中位线平行于α或在α内
C. 平面ABC必与α相交 D. 平面ABC必不垂直于α
10.已知A(-2,0),B(2,0),动点P与A、B两点连线的斜率分别为kPA和kPB,且满足kPA·kPB=t (t≠0且t≠-1).
(1)求动点P的轨迹C的方程;
(2)当t<0时,曲线C的两焦点为F1,F2,若曲线C上存在点Q使得∠F1QF2=120O,求t的取值范围.
解:(1) 设点P坐标为(x,y),依题意得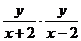 =t
=t y2=t(x2-4)
y2=t(x2-4)

 +
+ =1,轨迹C的方程为
=1,轨迹C的方程为 +
+ =1(x≠
=1(x≠ 2).
2).
(2) 当-1<t<0时,曲线C为焦点在x轴上的椭圆,
设|PF1|=r1,|PF2|=r2, 则r1+ r2=2a=4.
在△F1PF2中,|F1F2|=2c=4 , ∠F1PF2=120O,由余弦定理得
, ∠F1PF2=120O,由余弦定理得
4c2=r +r
+r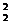 -2r1r2cos120°= r
-2r1r2cos120°= r +r
+r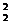 + r1r2= (r1+r2)2-r1r2≥(r1+r2)2-(
+ r1r2= (r1+r2)2-r1r2≥(r1+r2)2-( )2=3a2,
)2=3a2,
∴16(1+t)≥12, ∴t≥- .
.
所以当- ≤t<0时,曲线上存在点Q使∠F1QF2=120O
≤t<0时,曲线上存在点Q使∠F1QF2=120O
当t<-1时,曲线C为焦点在y轴上的椭圆,
设|PF1|=r1,|PF2|=r2, 则r1+ r2=2a= -4t,
在△F1PF2中,|F1F2|=2c=4 .∠F1PF2=120O,由余弦定理得
.∠F1PF2=120O,由余弦定理得
4c2=r +r
+r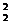 -2r1r2cos120°= r
-2r1r2cos120°= r +r
+r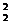 + r1r2= (r1+r2)2-r1r2≥(r1+r2)2-(
+ r1r2= (r1+r2)2-r1r2≥(r1+r2)2-( )2=3a2,
)2=3a2,
∴16(-1-t)≥-12t, ∴t≤-4.
所以当t≤-4时,曲线上存在点Q使∠F1QF2=120O
综上知当t<0时,曲线上存在点Q使∠AQB=120O的t的取值范围是
 .
.
9.求实数m的取值范围,使抛物线y2=x上存在两点关于直线y=m(x-3)对称
解法1:设抛物线上两点A(x1,y1),B(x2,y2)关于直线y=m(x-3)对称,A,B中点M(x,y),则当m=0时,有直线y=0,显然存在点关于它对称。
当m¹0时,
所以 ,所以M的坐标为
,所以M的坐标为 ,∵M在抛物线内,
,∵M在抛物线内,
则有 ,得
,得 且m¹0,综上所述,
且m¹0,综上所述,
解法2:设两点为A(x1,y1),B(x2,y2),它们的中点为M(x,y),两个对称点连线的方程为x=-my+b,与方程y2=x联立,得y2+my-b=0
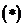
所以 y1+y2= -m,即 ,
,
又因为中点M在直线y=m(x-3)上,所以得M的坐标为
又因为中点M在直线x=-my+b上,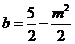 ,
,
对于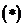 ,有D=m2+4b=10-m2>0,所以
,有D=m2+4b=10-m2>0,所以 。
。
8.如图3,抛物线y2=4x的一段与椭圆 的一段围成封闭图形,点
的一段围成封闭图形,点
 N(1,0)在x轴上,又A、B两点分别在抛物线及椭圆上,且AB//x轴,求△NAB
N(1,0)在x轴上,又A、B两点分别在抛物线及椭圆上,且AB//x轴,求△NAB
的周长l的取值范围。
解:易知N为抛物线y2=4x的焦点,又为椭圆的右焦点,
抛物线的准线l1:x=-1,椭圆的右准线l2:x=4,
过A作AC^l1于C,过B作BD^l2于D,
则C、A、B、D在同一条与x轴平行的直线上。
由 ,得抛物线与椭圆的交点M的横坐标
,得抛物线与椭圆的交点M的横坐标
 而|BN|=e|BD|=
而|BN|=e|BD|=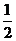 |BD|,|AN|=|AC|
|BD|,|AN|=|AC|
∴△NAB的周长l=|AN|+|AB|+|NB|=|BC|+|BN|
=|BC|+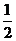 |BD|=|BC|+|BD|-
|BD|=|BC|+|BD|-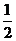 |BD|
|BD|
=|CD|-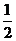 |BD|=5-
|BD|=5-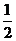 |BD|
|BD|
 ,即
,即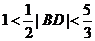
 ,即l的取值范围为(
,即l的取值范围为( ,4)
,4)
7.如图,已知A、B是椭圆 的两个顶点,
的两个顶点,
C、D是椭圆上两点,且分别在AB两侧,则四边形ABCD
面积的最大值是_______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com