
1.转化思想:
① 
② 将异面直线所成的角,直线与平面所成的角转化为平面角,然后解三角形
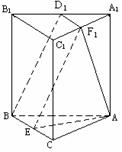
6.在棱长为 的正方体ABCD-A1B1C1D1, E、F分别为BC与A1D1的中点,
的正方体ABCD-A1B1C1D1, E、F分别为BC与A1D1的中点,
 (1) 求直线A1C与DE所成的角;
(1) 求直线A1C与DE所成的角;
(2) 求直线AD与平面B1EDF所成的角;
(3) 求面B1EDF 与 面ABCD所成的角。
[专家解答]
(1)如图,在平面ABCD内,过C作CP//DE交直
线AD于P,则 (或补角)为异面直线A1C与
(或补角)为异面直线A1C与
DE所成的角。在Δ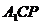 中,易得
中,易得
 ,由余弦定理得
,由余弦定理得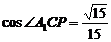 。
。
 故异面直线A1C与DE所成的角为
故异面直线A1C与DE所成的角为 。
。
(2)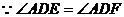 ,
,
∴AD在面B1EDF内的射影在∠EDF的平分线上。
而B1EDF是菱形,∴DB1为∠EDF的平分线。故直线
AD与面B1EDF所成的角为∠ADB1.在RtΔB1AD中,
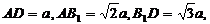 则
则 。
。
故直线AD与平面B1EDF所成的角为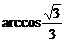 。
。
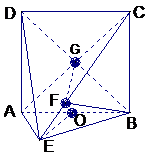
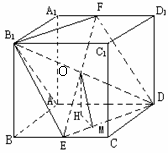 (3)连结EF、B1D,交于点O,显然O为B1D的中点,从而O为正方体ABCD-A1B1C1D1的中心,作OH⊥平面ABCD,则H为正方形ABCD的中心。再作HM⊥DE,垂足为M ,连结OM,则OM⊥DE(三垂线定理),故∠OMH为二面角B1-DE-A的平面角。
(3)连结EF、B1D,交于点O,显然O为B1D的中点,从而O为正方体ABCD-A1B1C1D1的中心,作OH⊥平面ABCD,则H为正方形ABCD的中心。再作HM⊥DE,垂足为M ,连结OM,则OM⊥DE(三垂线定理),故∠OMH为二面角B1-DE-A的平面角。
在RtΔDOE中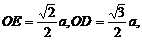
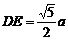 ,
,
则由面积关系得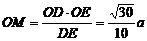 。
。
在RtΔOHM中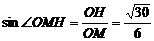 。
。
故面B1EDF 与 面ABCD所成的角为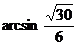
★★★高考要考什么
[考点透视]
异面直线所成角,直线与平面所成角,求二面角每年必考,作为解答题可能性最大.
[热点透析]
5.PA,PB,PC是从P点引出的三条射线,他们之间每两条的夹角都是60°,则直线PC与平面PAB所成的角的余弦值为 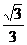 .
.
4.已知正四棱锥的体积为12,底面对角线的长为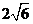 ,
,
则侧面与底面所成的二面角等于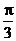 .
.
3.直三棱住A1B1C1-ABC,∠BCA= ,点D1、F1 分
,点D1、F1 分
别是A1B1、A1C1的中点,BC=CA=CC1,则BD1与AF1
所成角的余弦值是( A )
A.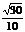 B.
B.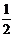 C.
C.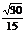 D.
D.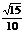
2.在一个450的二面角的一个平面内有一条直线与二面角棱成450角,则此直线与
 二面角的另一个面所成的角为 ( A
)
二面角的另一个面所成的角为 ( A
)
A.300 B.450 C.600 D.900
1.如图,直线a、b相交与点O且a、b成600,过点O 与a、
b都成600角的直线有( C )
A.1 条 B.2条 C.3条 D.4条
8.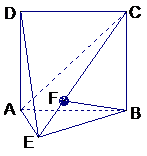 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B-AC-E的大小;
(Ⅲ)求点D到平面ACE的距离.
解:(I)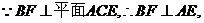
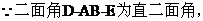


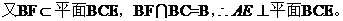
(II)连结AC、BD交于G,连结FG,
∵ABCD为正方形,∴BD⊥AC, ∵BF⊥平面ACE,
∴FG⊥AC,∠FGB为二面角B-AC-E的平面角,由(I)可知,AE⊥平面BCE,
∴AE⊥EB,又AE=EB,AB=2,AE=BE=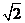 ,
,
在直角三角形BCE中,CE=
在正方形中,BG=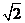 ,在直角三角形BFG中,
,在直角三角形BFG中,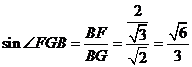
 ∴二面角B-AC-E为
∴二面角B-AC-E为

(III)由(II)可知,在正方形ABCD中,BG=DG,
D到平面ACB的距离等于B到平面ACE的距离,BF⊥平
面ACE,线段BF的长度就是点B到平面ACE的距离,即
为D到平面ACE的距离.故D到平面的距离为 .
.
另法:过点E作 交AB于点O. OE=1.
交AB于点O. OE=1.
∵二面角D-AB-E为直二面角,∴EO⊥平面ABCD.
设D到平面ACE的距离为h,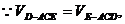
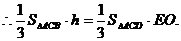
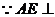 平面BCE,
平面BCE,
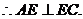
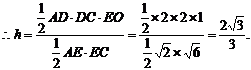
∴点D到平面ACE的距离为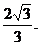
解法二:(Ⅰ)同解法一.
(Ⅱ)以线段AB的中点为原点O,OE所在直线为x轴,AB所在直线为y轴,过O点平行于AD的直线为z轴,建立空间直角坐标系O-xyz,如图.
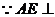 面BCE,BE
面BCE,BE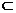 面BCE,
面BCE, 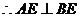 ,
,
在 的中点,
的中点,

 设平面AEC的一个法向量为
设平面AEC的一个法向量为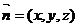 ,
,
则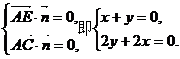 解得
解得
令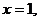 得
得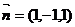 是平面AEC的一个法向量.
是平面AEC的一个法向量.
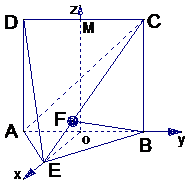 又平面BAC的一个法向量为
又平面BAC的一个法向量为 ,
,
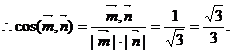
∴二面角B-AC-E的大小为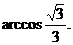
(III)∵AD//z轴,AD=2,∴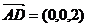 ,
,
∴点D到平面ACE的距离

7.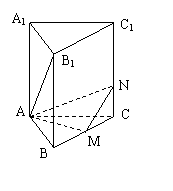 如图,正三棱柱ABC-A1B1C1的所有棱长都为a,M是BC的中点,N是CC1上一点,满足MN⊥AB1。
如图,正三棱柱ABC-A1B1C1的所有棱长都为a,M是BC的中点,N是CC1上一点,满足MN⊥AB1。
(1) 试确定点N的位置;
(2) 求点C1到平面AMN的距离。
解 (1)∵M是BC中点,ABC-A1B1C1为正三棱柱,
∴AM⊥平面B1BCC1, ∴AM⊥MN,
∵MN⊥AB1, ∴MN⊥平面B1AM, ∴MN⊥B1N,
设NC=x,在RtΔB1BM中,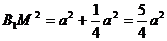 ,
,
在RtΔNCM中, ,
,
在RtΔB1C1N中, , 在RtΔB1MN中,
, 在RtΔB1MN中,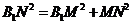 ,
,
∴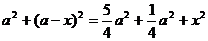 , ∴
, ∴ , ∴N在CC1的
, ∴N在CC1的 处。
处。
(2)点C1到平面AMN的距离,即为三棱锥C1-AMN的高,
设为h,则 ,
,
∵ ,∴
,∴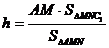 ,
,
∵AM=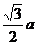 ,MN=
,MN= , ∴
, ∴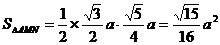 ,
,
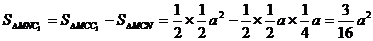 , ∴
, ∴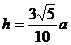 .
.
6.已知平面a与平面b交于直线l,P是空间一点,PA⊥a,垂足为A,PB⊥b,
垂足为B,且PA=1,PB=2,若点A在b内的射影与点B在a内的射影重合,
则点P到l的距离 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com