
(13)已知点P在抛物线 上运动,定点A(0,-1),若点M分
上运动,定点A(0,-1),若点M分 所成的比为2,则动点M的轨迹方程是
.
所成的比为2,则动点M的轨迹方程是
.
(14) 一辆列车沿直线轨道前进,从刹车开始到停车这段时间内,测的刹车后 秒内列车前进的距离为
秒内列车前进的距离为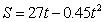 米,则列车刹车后 秒车停下来,期间列车前进了 米.
米,则列车刹车后 秒车停下来,期间列车前进了 米.

(16) 设有两个命题: ① 不等式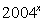 + 4 >m> 2x-x2对一切实数x恒成立;
+ 4 >m> 2x-x2对一切实数x恒成立;
② 函数f(x)=-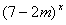 是R上的减函数.
是R上的减函数.
使这两个命题都是真命题的充要条件,用m可表示为 .
(1)计算: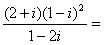 ( )
( )
(A)2 (B) (C)
(C)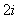 (D)
(D)
(2)已知 ,则
,则 在
在 上的射影为
上的射影为
(A) 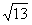 ; (B)
; (B)  ; (C)
; (C) 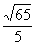 ; (D)
; (D) 

(3)已知a、b为直线,α、β为平面.在下列四个命题中,
① 若a⊥α,b⊥α,则a∥b ; ② 若 a∥α,b ∥α,则a∥b;
③ 若a⊥α,a⊥β,则α∥β; ④ 若α∥b,β∥b ,则α∥β.
正确命题的个数是
(A) 1 (B) 3 (C) 2 (D) 0
(4)函数f(x)=A·tan(ωx+φ)(φ>0)在区间[m,n]上的函数值都小于0,则函数g(x)=A·cot(ωx+φ)在[m,n]上的函数值
(A) 都大于0,且有最大值为g(m) (B) 都小于0,且有最大值为g(m)

(6)对于四条曲线:①  ;②
;②  ;③
;③  ;
;
④  . 其中与直线2 x + y +3=0有交点的所有曲线是
. 其中与直线2 x + y +3=0有交点的所有曲线是
(A) ②,③,④ (B) ①,② (C) ②,④ (D) ①,②,③
(7)将4名司机和8名售票员分配到四辆公共汽车上,每辆车上分别有1名司机和2名售票员,则可能的分配方案种数是
(A) (B)
(B) (C)
(C) (D)
(D)
(8)定义在R上的偶函数f(x)在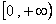 上递增,
上递增, ,则满足
,则满足 >0的x的取值范围是
>0的x的取值范围是
(A) (B)
(B) (C)
(C) 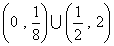 (D)
(D) 
(9)现有一个长方体水箱,从水箱里面量得它的深是30cm,底面的长是25cm,宽是20cm.设0< a ≤8,水箱里盛有深为a cm的水,若往水箱里放入棱长为10cm的立方体铁块,则水深为
(A) 2 cm
(B) 10 cm
(C) (a+2) cm
(D) 
(10)我国首航员杨利伟乘坐的“神舟五号”载人宇宙飞船的运行轨道是以地球的中心F为一个焦点的椭圆,近地点A距地面为m公里,远地点B距地面为n公里.若地球的半径为R公里,则飞船运行轨道的短轴长为
(A) mn (B) 2 (C) 2nm (D)
(C) 2nm (D) 
(11)已知函数f(x)的图象过点(0,-5),它的导数f /(x)=4x3-4x,则当f(x)取得最大值-5时,x的值应为
(A) -1 (B) 0 (C) 1 (D) ±1
(12)在平面直角坐标系中,有两个区域M、N,M是由三个不等式y≥0、y≤x和y≤2-x确定的;N是随t变化的区域,它由不等式t≤x≤t+1(0≤t≤1)所确定.设M、N的公共部分的面积为f(t),则f(t)等于
(A) (B)
(B) (C)
(C) (D)
(D) 
16、如图所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,M=3m,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:
①A、B最后的速度大小和方向;
②要使A最终不脱离B,平板车B的最短长度为多少
③从地面上看,小木块向左运动到离出发点最远处时,平板车向右运动的位移大小.

15、如图,竖直平面内的3/4圆弧形光滑轨道半径为R=2.5m,其A端与圆心O等高,AD为水平面,B点在O的正上方。一个质量为m=0.5kg的小球在A点正上方P点由静止释放,自由下落至A点进入圆弧轨道,从B点平抛落到C点,已知O,A,C在一条直线上,且AC=R,g=10m/s2,
求:①小球落到C点前瞬间,速度的大小是多少?
②小球过B点时,对轨道的作用力的大小和方向。
③高度PA是多少?
14、排球运动是一项同学们喜欢的体育运动.为了了解排球的某些性能,某同学让排球从距地面高h1=1.8 m处自由落下,测出该排球从开始下落到第一次反弹到最高点所用时间为t=1.3 s,第一次反弹的高度为h2=1.25 m.已知排球的质量为
m=0.4 kg,g取10 m/s2,不计空气阻力.求:
①排球与地面的作用时间.
②排球对地面的平均作用力的大小.

13、一个物体在地面上受到的重力为160N,将它放置在航天飞机中,当航天飞机以加速度a=5m/s2随火箭竖直向上加速升空的过程中,某时刻测得物体与航天飞机中的支持物在竖直向上的相互挤压力为90N,(地球的半径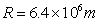 ,g=10m/s2)求此时
,g=10m/s2)求此时
①航天飞机所在高度的重力加速度
②航天飞机距离地面的高度。
12、为了测定一根轻弹簧压缩到最短时储存的弹性势能大小,可以将弹簧固定在一个带有光滑凹槽的直轨道的一端,并将轨道固定在水平桌面的边缘上,如图所示,用钢球将弹簧压缩至最短,而后突然释放,钢球将沿轨道飞出桌面,实验时:
(1)需要直接测定的物理量是 、 、 。
(2)计算弹簧压缩到最短时弹性势能的关系式是Ep= .(用直接测量的量表示)
11、在“验证机械能守恒定律”的实验中,已知打点计时器所用电源的频率为50 Hz,查得当地的重力加速度g=9.80 m/s2,测得所用的重物的质量为1.00 kg,实验中得到一条点迹清晰的纸带,如图所示,把第一个点记作O,另选连续的4个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分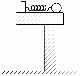 别为62.99 cm、70.18 cm、77.76 cm、85.73 cm,根据以上数据,可知重物由O点运动到C点,重力势能的减少量等于_______J,动能的增加量等于_______J.(取三位有效数字)
别为62.99 cm、70.18 cm、77.76 cm、85.73 cm,根据以上数据,可知重物由O点运动到C点,重力势能的减少量等于_______J,动能的增加量等于_______J.(取三位有效数字)

10、一辆汽车以额定功率在平直的公路上行驶,经过3min,速度由36km/h提高到72km/h,则在这段时间内,汽车驶过的路程[ ]
A.一定大于2.7km,小于3.6km B.一定小于2.7km
C.可能大于3.6km D.上述情况均可能
第Ⅱ卷
(注:所有答案全部答在答题卡上)
9、质量为m的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v匀速运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从静止释放到相对静止这一过程,下列说法正确的是[ ]
A.电动机多做的功为 B.物体在传送带上的划痕长
B.物体在传送带上的划痕长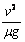
C.传送带克服摩擦力做的功为 D.电动机增加的功率为
D.电动机增加的功率为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com