2．函数值域的求法：①分析法 ；②配方法 ；③判别式法 ；④利用函数单调性 ；

⑤换元法 ；⑥利用均值不等式 ； ⑦利用数形结合或几何意义(斜率、距离、绝对值的意义等)；⑧利用函数有界性(、、等)；⑨导数法

1．映射：注意 ①第一个集合中的元素必须有象；②一对一，或多对一。

3．(1)含n个元素的集合的子集数为2ⁿ,真子集数为2ⁿ－1；非空真子集的数为2ⁿ-2；

(2) 注意：讨论的时候不要遗忘了的情况；

(3)。

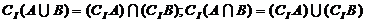2．数形结合是解集合问题的常用方法：解题时要尽可能地借助数轴、直角坐标系或韦恩图等工具，将抽象的代数问题具体化、形象化、直观化，然后利用数形结合的思想方法解决；是任何集合的子集，是任何非空集合的真子集。

1．理解集合中元素的意义是解决集合问题的关键：元素是函数关系中自变量的取值？还是因变量的取值？还是曲线上的点？… ；

例1．如图所示，恒定的拉力大小F=8N，方向与水平线夹θ=60°角，拉着绳头

使物体沿水平面移动 =2m的过程中，拉力做了多少功？

分析：常会有同学做这样的分析与计算：力的大小为S= 　=2m，力与位移的方向间夹角为60°，所以：

其实，这样的计算是错误的。

解答：如图12-2所示，随着物体沿水平面前进 =2m，绳头从A点被拉到B点，由此可见：拉F所作用的物体(绳头)的位移S可由几何关系求得为

而力F与位移S间的夹角为　　　　　　　　　　　　　　　　　　　　　　

所以，这过程中拉F作用于绳头所做的功为　　　　　　　　　　　　　　　　　

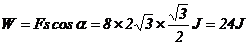
例2．质量为　m=1kg的物体以v₀=10m/s的速度水平抛出，空气阻力不计，取g=10m/s²,则在第1s内重力做功为________________J；第1s内重力做功的平均功率为__________W；第1s末重力做功的瞬时功率为____________W；第1s内物体增加的动能为____________J；第1s内物体减少的重力势能____________J。

分析：此道题考察了功、功率、动能、重力势能等概念以及与上述概念相关的动能定理，机械能守恒定律等规律。

解答：重力做的功等于重力与物体沿重力方向(竖直方向)上位移的乘积，而第1s内物体沿竖直方向的位移为

所以有：

由平均功率的定义得

瞬时功率一般计算可用力与力的方向上的瞬时速度的相乘而得，第1s末物体沿重力方向上的速度为

所以有

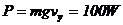
考虑到平抛运动过程中只有重力做功，于是由动能定理得

又由于只有重力做功其机械能守恒，增加的动能应与减少的重力势能相等。于是又可直接得

此例应依次填充：50；50；100；50；50。

例3：质量4t的机车，发动机的最大输出功率为100kW，运动阻力恒为，试求；

(1)当机车由静止开始以0.5m/s²的加速度沿水平轨道做匀加速直线运动的过程中，能达到的最大速度和达到该最大速度所需的时间。

(2)若机车保持额定功率不变行驶，能达到的最大速度以及速度为10m/s时机车的加速度。

　 分析：注意到机车匀加速运动所能达到的最大速度V_m和机车在运动形式不加制约时所能达到的最大速度一般是不同的。

解答：(1)机车做匀加速直线运动时，有

　　　 F- 　=

　　　 P=FV_m

　　　 V_m=at

由此可解得

　　　　 V_m=25m/s

　　　　　 t=50s

(2)机车行驶时运动形式不加限制而机车输出功率保持额定功不变时则可在大小等于阻力牵引力作用下做匀速直线运动，此时又有

由此又可解得

例4：如图所示，小滑块从斜面顶点A由静止滑至水平部分C点而停止。已知斜面高为h，滑块运动的整个水平距离为s设斜面和水平部分与小滑块的动摩擦因数相同，求此动摩擦因数

分析：可以运动动能定理分析求解：

解答：取物体为研究对象，考察人A处静止释放下直至到C点处于　　　　　

静止的过程，运动动能定理有。

由此即可求得

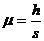
例5：如图12-4所示，一固定的楔形木块，其斜面的倾角，另一边与地面垂直，顶上有一定滑轮。一柔软的细线跨过定滑轮，两端分别与物块A和B连结，A的质量为4m，B的质量为m。开始时将B按在地面上不动，　 然后放开手,让A沿斜面下滑而B上升.物块A与斜面间无摩擦.设当A沿斜面下滑s距离后,细线突然断了.求物块B上升的最大高度H.　　　　　　　　　　　　　　　　　　

分析：可以运用机械能守恒定律分析求解

解答：取A与B构成的系统为研究对象，考察以刚放手起直到强刚断的过程，这过程中系统的机械能守恒。有

再取B为研究对象，考察从强刚断直到B升至最高点的过程，这过程中B的机械能守恒，又有

而B所上升的最大高度为

H= 　+s

由此即得

H=1.2s

4、机械能守恒定律。

(1)机械能：动能和势能的总和称机械能。而势能中除了重力势能外还有弹性势能。所谓弹性势能批量的是物体由于发生弹性形变而具有的能。

(2)机械能守恒守律：只有重力做功时，动能和重力势能间相互转换，但机械能的总量保持不变，这就是所谓的机械能守恒定律；只有弹力做功时，动能和弹性势能间相互转换，机械能的总量也保持不变，这也叫机械能守恒定律。

(3)机械能守恒的条件：只有重力和系统内弹力做功，则系统的机械能总量将保持不变。

3、重力做功的特点与重力势能。

　　 (1)重力做功的特点：重力做功与路径无关，只与始末位置的竖直高度差有关，当重力为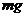的物体从A点运动到B点，无论走过怎样的路径，只要A、B两点间竖直高度差为，重力所做的功均为

(2)重力势能：物体由于被举高而具有的能叫重力势能。其表达式为：

其中h为物体所在处相对于所选取的零势面的竖直高度，而零势面的选取可以是任意的，一般是取地面为重力势能的零势面。

由于零势面的选取可以是任意的，所以一个物体在某一状态下所具有的重力势能的值将随零势面的选取而决定，但物体经历的某一上过程中重力的势能的变化却与零势面的选取无关。

(3)重力做功与重势能变化间的关系：重力做的功总等于重力势能的减少量，即

2、动能和动能定理

(1)动能概念的理解：物体由于运动而具有的能叫动能，其表达式为：

和动能一样，动能也是用以描述机械运动的状态量。只是动量是从机械运动出发量化机械运动的状态动量确定的物体决定着它克服一定的阻力还能运动多久；动能则是从机械运动与其它运动的关系出发量化机械运动的状态，动能确定的物体决定着它克服一定的阻力还能运动多远。

(2)动能定理：外力所做的总功等物体动能的变化量。动能定理实际上是在牛顿第二定律的基础上对空间累积而得：在牛顿第二定律

　　 F=

两端同乘以合外力方向上的位移要，即可得

和动量定理相似，动能定理也建立起过程量(功)与状态量(动能)变化间的关系，利用这一关系，也可以通过比较状态达到了解过程之目的。

1、功的四个基本问题。

　 涉及到功的概念的基本问题，往往会从如下四个方面提出。

　 (1)做功与否的判断问题：物体受到力的作用，并在力的方向上通过一段位移，我们就说这个力对物体做了功。由此看来，做工功与否的判断，关键看功的两个必要因素，第一是力；第二是力的方向上的位移。而所谓的“力的方向上的位移”可作如下理解：当位移平行于力，则位移就是力的方向上的位的位移；当位移垂直于力，则位移垂直于力，则位移就不是力的方向上的位移；当位移与力既不垂直又不平行于力，则可对位移进行正交分解，其平行于力的方向上的分位移仍被称为力的方向上的位移。

　 (2)做功多少的计算问题：做功多少的计算可直接应用功的公式。

W=FS cosα

　 公式中F是做功的力；S是F所作用的物体发生的位移；而α则是F与S间的夹角。至于变力做功的计算，通常可以利用功能关系通过能量变化的计算来了解变力的功。

　 (3)做功快慢的描述问题：做功快慢程度引入功率来描述，其定义式为：

P=W/t

　 功率的计算有时还可利用形如

P=Fv

　 (4)做功意义的理解问题：做功意味着能量的转移与转化，做多少功，相应就有多少能量发生转移或转化。