3. 如图所示，有一水平放置的绝缘光滑圆槽，圆半径为R，处在一水平向右且与圆槽直径AB平行的匀强电场中，场强为E．圆槽内有一质量为m，带电量为+q的小球作圆周运动，运动到A点时速度大小为v，则到达B点时小球的向心加速度大小为__________________；小球做完整的圆周运动最难通过图中的_____________点。

点拨：竖直平面内的圆周运动问题。

由动能定理：

解得：

因为小球在水平面内通过A点的速度最小，因此通过A点最困难。

2. 在大风的情况下，一小球自A点竖直向上抛出，其运动的轨迹如图11所示(小球的运动可看作竖直方向的竖直上抛运动和水平方向的初速YC为零的匀加速直线运动的合运动)。小球运动的轨迹上A、B两点在同一水平线上，M点为轨迹的最高点。若风力的大小恒定、方向水平向右，小球抛出时的动能为4J，在M点时它的动能为2J，不计其他的阻力。求：

(1)小球的水平位移S₁与S₂的比值。

(2)小球所受风力F与重力G的比值。(结果可用根式表示)

(3)小球落回到B点时的动能E_KB-

点拨：平抛(或类平抛问题)

(1)小球在竖直方向上做竖直上抛运动，故从A点至M点和从M点至B点的时间t相等，小球在水平方向上做初速为零的匀加速运动，设加速度为a，则

　　 　　　所以

　 (2)小球从A点至M点，水平方向据动量定理F·t=mv_M－0

竖直方向据动量定理　 －Gt=0－mv_A

另据题意　　 　，联立式解得

　 (3)小球在水平方向上　

动能

针对典型精析的例题题型，训练以下习题。

1. 如图甲所示，在一端封闭、长约lm的玻璃管内注满清水，水中放一个蜡烛做的蜡块，将玻璃管的开口端用胶塞塞紧．然后将这个玻璃管倒置，在蜡块沿玻璃管上升的同时，将玻璃管水平向右移动．假设从某时刻开始计时，蜡块在玻璃管内每1s上升的距离都是10cm，玻璃管向右匀加速平移，每1s通过的水平位移依次是2.5cm、7.5cm、12.5cm、17.5cm．图乙中，y表示蜡块竖直方向的位移，x表示蜡块随玻璃管通过的水平位移，t=0时蜡块位于坐标原点．取重力加速度g=10m/s²

(1)请在图乙中画出蜡块4s内的轨迹；

(2)求出玻璃管向右平移的加速度；

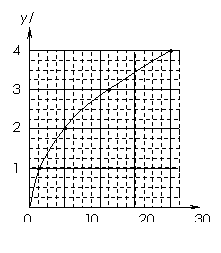(3)求t=2s时蜡块的速度v．

点拨：运动的合成与分解问题。

(1)如图　(4分)

(2)Δx=at² ①(2分)

a= ②(2分)

(3)v_y=　 ③(1分)

v_x=at=0.1m/s　　　　 ④(1分)

v=　⑤(2分

2.　　　 要注意库仑力始终与运动方向垂直，不做功。

题型4.(万有引力定律及应用)图示是我国的“探月工程”向月球发射一颗绕月探测卫星“嫦娥一号”过程简图．“嫦娥一号”进入月球轨道后，在距离月球表面高为h的轨道上绕月球做匀速圆周运动．

(1)若已知月球半径为R_月，月球表面的重力加速度为g_月，则“嫦娥一号”环绕月球运行的周期为多少？

(2)若已知R_月=R_地，g_月=g_地，则近月卫星的运行速度约为近地卫星运行速度的多少倍？

解析：(1)设“嫦娥一号”环绕月球运行的周期是T，根据牛顿第二定律得

G= mg_月 　(2分)

G= m(R_月+h)(2分)

解得T=(2分)

(2)对于靠近天体表面的行星或卫星有mg=，v=(2分)

由v=知，=(1分)

将R_月=R_地，g_月=g_地代入计算，可知(≈0.2)(2分)

即近月卫星的运行速度约为近地卫星运行速度的(0.2)倍．

规律总结：在利用万有引力定律解决天体运动的有关问题是，通常把天体运动看成匀速圆周运动，其需要的向心力就是天体之间相互作用的万有引力提供。

即

题型5.(卫星与航天问题)如图所示，A为静止于地球赤道上的物体，B为绕地球做椭圆轨道运行的卫星，C为绕地球做圆周运动的卫星，P为B、C两卫星轨道的交点．已知A、B、C绕地心运动的周期相同．相对于地心，下列说法中不正确的是

A．物体A和卫星C具有相同大小的加速度

C．可能出现：在每天的某一时刻卫星B在A的正上方

D．卫星B在P点的运行加速度大小与卫星C的运行加速度大小相等

解析：A、C两者周期相同，转动角速度 相同，由可知A错；由可知，，B正确；因为物体A随地球自转，而B物体转动周期与A相同，当B物体经过地心与A连线与椭圆轨道的交点是，就会看到B在A的正上方，C对；由可知，，D正确。

题型6.(天体与航天器的能量问题)重力势能E_P＝mgh实际上是万有引力势能在地面附近的近似表达式，其更精确的表达式为E_P＝－GMm/r，式中G为万有引力恒量，M为地球质量，m为物体质量，r为物体到地心的距离，并以无限远处引力势能为零 现有一质量为m的地球卫星，在离地面高度为H处绕地球做匀速圆周运动。已知地球半径为R，地球表面的重力加速度为g，地球质量未知，试求：

(1)卫星做匀速圆周运动的线速度；

(2)卫星的引力势能；

(3)卫星的机械能；

(4)若要使卫星能依靠惯性飞离地球(飞到引力势能为零的地方)，则卫星至少要具有多大的初速度？

解析：(1)由牛顿运动定律： (2分)

　得：(1分)

⑵由引力势能的表达式：(2分)

⑶卫星的机械能应该是卫星的动能和势能之和，即

得(3分)

(1分)

⑷由机械能守恒定律，对地球与卫星组成的系统，在地球表面的机械能与飞到无限远处的机械能相等。设初速度至少应为v

，(2分)

解得：(1分)

规律总结：在卫星和地球组成的系统内，机械能是守恒的，卫星的动能可通过匀速圆周运动的线速度来求，引力势能在选择了无穷远处为零势能点后，可以用 来求，机械能为两者之和。

1.　　　 在处理竖直平面内的圆周运动问题时，一般要用动能定理建立最高点、最低点的速度关系。

3.区分分运动和合运动的基本方法是：合运动是物体的实际运动轨迹。

题型2. (平抛(或类平抛)运动问题)如图所示,AB为竖直墙壁，A点和P点在同一水平面上。空间存　在着竖直方向的匀强电场。将一带电小球从P点以速度向A抛出，结果打在墙上的C处。若撤去电场，将小球从P点以初速向A抛出，也正好打在墙上的C点。求：

(1)第一次抛出后小球所受电场力和重力之比

(2)小球两次到达C点时速度之比

解析：(1)设AC=h、电场力为F_Q，根据牛顿第二定律得：F_Q+mg=ma①

第一次抛出时，h= 　　②　 (1分 )

第二次抛出时，h=　 ③ (1分 )

由②、③两式得a=4g　　　 ④ (1分 )

所以，F_Q：G=3:1　　　　　 ⑤ (1分 )

(2)第一次抛出打在C点的竖直分速度_y1=a()⑥ (1分 )

第二次抛出打在C点的竖直分速度_y2=g()⑦ (1分 )

第一次抛出打在C点的速度₁=⑧ (1分 )

第二次抛出打在C点的速度₂=⑨ (1分 )

所以，₁：₂=2：1⑩ (1分 )

规律总结：平抛(或类平抛)运动处理的基本方法就是把运动分解为水平方向的匀速运动和竖直方向的匀加速运动。通过研究分运动达到研究合运动的目的。

题型3.(竖直平面内的圆周运动问题)如图15所示，质量为 m、电量为+q的带电小球固定于一不可伸长的绝缘细线一端，绳的另一端固定于O点，绳长为，O点有一电荷量为+Q(Q＞＞q)的点电荷P，现加一个水平和右的匀强电场，小球静止于与竖直方向成 θ=30⁰角的A点。求：

(1)小球静止在A点处绳子受到的拉力；

(2) 外加电场大小；

(3)将小球拉起至与O点等高的B点后无初速释放，则小球经过最低点C时，绳受到的拉力

解析：(1)带电粒子A处于平衡，其受力如图，其中F为两点电荷间的库仑力，T为绳子拉力，E₀为外加电场，则

Tcosθ-mg-Fcosθs=0　　 1 (2分)

Fsinθ+qE₀-Tsinθ=0　　　 2 (2分)

　　　　 　　　3 (2分)

联立式解得：有 　　　4 (2分)

　　　　　　 　　5 (2分)

(2)小球从B运动到C的过程中，q与Q间的库仑力不做功，由动能定理得

　 6 (2分)

在C点时：　 　7 (2分)

联立5、6、7解得： 　　8 (2分)

审题指导：1.要注意对小球受力分析，不要漏掉库仑力。

题型1.(运动的合成与分解问题)若河水的流速大小与水到河岸的距离有关，河中心水的流速最大，河岸边缘处水的流速最小。现假设河的宽度为120m，河中心水的流速大小为4m/s，船在静水中的速度大小为3m/s，要使般以最短时间渡河，则　　　　　　　　　　　 (　　 　　)

　　 A．船渡河的最短时间是24s

　　 B．在行驶过程中，船头始终与河岸垂直

　　 C．船在河水中航行的轨迹是一条直线

　　 D．般在河水中的最大速度为5m/s

解析：根据分运动具有独立性和等时性可知，当船头与河岸垂直过河时，时间t最短，t=120/3=40s，A错，B对；船速是恒定的，但是水流速度与水到河岸的距离有关，合速度的大小和方向都在不断变化，轨迹为曲线，C错；船在河水中的速度是指合运动的速度最大，D正确。

规律总结：1.合运动与分运动具有等时性，分运动具有独立性，这一原理经常应用解决小船过河即平抛运动问题。

2.运动的合成与分解的依据仍然是平行四边形定则。

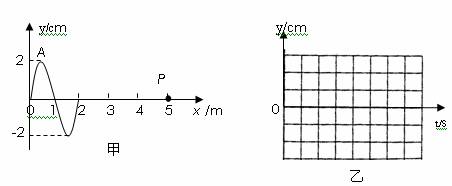
20.(9分)一列简谐波沿x轴正方向传播，t=0时波形如图甲所示.已知在0.6s末，A点恰第四次(图中为第一次)出现在波峰，求

(1)该简谐波波长、波速分别为多少？

(2)x=5m处的质点p第一次出现波峰的时间为多少？

(3)如果以该机械波传到质点p开始计时，请在下图乙中画出p点的振动图像，并标明必要的数字，至少画出一个周期的图像。

19.(8分)如图所示是一列横波上A、B两质点的振动图象，该波由A传向B，两质点沿波的传播方向上的距离Δx=4.0m，波长大于3.0m，求这列波的波速。

18. (5分)一列沿x轴正方向传播的横波，某时刻的波形图象如图中的实线Ⅰ所示，经t＝0.2 s后，波形图象如图中虚线Ⅱ所示．求这列波的波速。