
空间曲线可以看成是两个曲面的交线,因此,两个相交曲面的方程构成的方程组表示空间曲线,方程组  (两个曲面的交线)称为空间曲线的一般方程。
(两个曲面的交线)称为空间曲线的一般方程。
 如:
如:  表示平面
表示平面  上的一个圆,圆心在
上的一个圆,圆心在 ,半径
,半径  。
。
注:空间曲线的一般方程形式不唯一。如上面的圆也可用方程组 来表示。
来表示。

 例1 方程组
例1 方程组  表示怎样的曲线?
表示怎样的曲线?
解  表示球心在原点,半径为
表示球心在原点,半径为 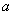 的上半球面,
的上半球面, 表示母线平行于
表示母线平行于  轴的圆柱面,其交线见图。
轴的圆柱面,其交线见图。
3.  ;
;
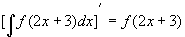 。
。

设  是单调可导函数,且
是单调可导函数,且
 ;又
;又
 具有原函数
具有原函数
 ,则有
,则有

其中  为
为
 的反函数。
的反函数。
例24 

解 采用三角代换  ,(
,( ),则
),则

原式= 



( 因为  )
)

例25 

解 作三角代换 
原式= 

为了将 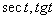 化成
化成
 的函数,作一直角三角形,使它的一个锐角为
的函数,作一直角三角形,使它的一个锐角为
 ,根据所用代换
,根据所用代换
 找出对边
找出对边
 与邻边
与邻边
 ,则斜边为
,则斜边为
 (见图),
(见图),

所以 
原式= 
(其中  )
)
例26 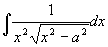

解  时(
时( 时可得同样结果),
时可得同样结果),

作三角代换

原式= 
= 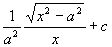
例27 
解 用倒代换,令  ,则
,则

原式= 

从上面例题可看出:如果被积函数中含有因子  、
、
 、
、
 时,可分别采用三角代换
时,可分别采用三角代换
 、
、
 、
、
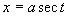 化去根号后再积分。根据去根号的思想也可得到简单无理函数的积分方法,看下面例题
化去根号后再积分。根据去根号的思想也可得到简单无理函数的积分方法,看下面例题
例28 
解 去根号,令  ,
,
 ,
,

原式= 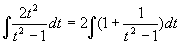

例29 
解 令  ,
,

原式  =
= 
分部积分法
设函数 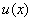 、
、
 具有连续导数,则由
具有连续导数,则由
 移项
移项 
两边积分得分部积分公式
 或
或 
例1 
解 使用分部积分公式时,正确的选择 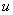 和
和
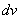 十分重要
十分重要
设  ,得
,得
原式= 
如果设  ,
,
 ,得
,得
原式= 
上式右端积分比左端更不易算出,一般 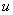 和
和
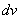 的选择要考虑两点:
的选择要考虑两点:
(1)  要容易求出;
要容易求出;
(2)  要比
要比  容易积出。
容易积出。
例2 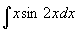
解 设 
原式= 

例3 
解 设 
原式= 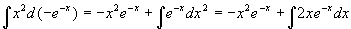
(再用一次分部积分公式)



例4 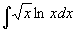
解 设 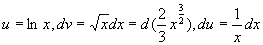
原式= 
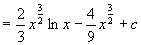
例5 
解 设 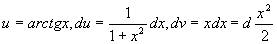
原式= 

例6 
解 设 
原式= 


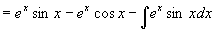
将右边积分移到左边

注:由上面例子可看出下面三种类型的积分要用分步积分法
类型 ,
,
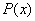 为多项式,
为多项式,
 ,
,
 选
选

类型Ⅱ: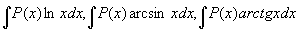 ,
,
 ;
;
选  等。
等。
类型Ⅲ: ,
,
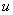 和
和
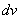 任选均可。
任选均可。
分步积分法使用熟练后, 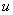 和
和
 不必写出。分步积分法也可以用来计算其他某些积分。
不必写出。分步积分法也可以用来计算其他某些积分。
例7 求  (其中
(其中
 为正整数)
为正整数)
解 

而 






 (递推公式)
(递推公式)

例8 

例9 已知:  是
是
 的一个原函数,求:
的一个原函数,求:

解 因  是
是
 的一个原函数
的一个原函数


下面再举几个换元法与分步积分法结合使用的例子
例10 
解 


例11 
解 
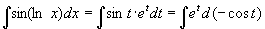



例12  (令
(令  )
)
2.  ,
, 表示对中间变量
表示对中间变量
 求导。
求导。
定义:两个矢量  与
与  的矢量积仍是一个矢量,
的矢量积仍是一个矢量,

记作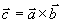 ,其模为
,其模为 ,其方向由
,其方向由 到
到  按右手法则决定,且
按右手法则决定,且 。
。
即  ,
, 且
且
注:矢量积的结果是矢量。
运算性质:(1)反交换律
(2)结合律
(3)分配律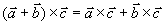
两个结论:(1)
(2)两个非零矢量 与
与 平行的充要条件是
平行的充要条件是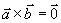
即 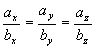
注: 在几何上表示以矢量
在几何上表示以矢量  为邻边的平行四边形的面积。
为邻边的平行四边形的面积。

矢量积的坐标表达式 设  ,
,  则
则



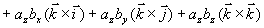

所以

例6 设 求
求 。
。
解 



例7 设 求与
求与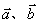 都垂直的单位矢量
都垂直的单位矢量  。
。
解  与
与  和
和 都是垂直的,
都是垂直的,

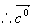


例8 设 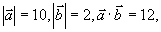 求
求  。
。
解 

 ,
,
例9 设 与
与 的夹角为
的夹角为
 ,
, ,求
,求 。
。
解 
例10 设 与
与 的夹角为
的夹角为  ,
, ,求
,求 。
。
例11 求以  三点为顶点的三角形面积。
三点为顶点的三角形面积。
解 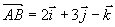 ,
, 


所以,三角形面积为

设一物体在常力 作用下沿直线从点O移动到点P,则物体的位移
作用下沿直线从点O移动到点P,则物体的位移  ,力
,力 所做的功
所做的功 。
。
定义:两个矢量  与
与 的模与其夹角
的模与其夹角  的余弦之积称为
的余弦之积称为 与
与 的数量积(或称内积、点积),记作
的数量积(或称内积、点积),记作
 既
既 或
或
运算性质:
(1)交换律
(2)结合律 
(3)分配律
其中  为常数。
为常数。
两个结论:
(1)
(2)两个非零矢量 与
与 相互垂直的充要条件是
相互垂直的充要条件是  既
既

注:规定零矢量与任何矢量垂直,所以两矢量 与
与  垂直的充要条件是
垂直的充要条件是  .
.
数量积的坐标表达式 设  ;
;

则

两矢量夹角的余弦为( ,
,  均为非零矢量)
均为非零矢量)
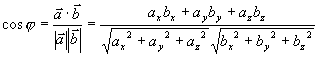
或 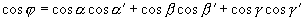
其中  为
为 的方向角,
的方向角,  为
为  的方向角。
的方向角。
例1 设 ,
, ,求
,求  。
。
解 

例2 已知三点  求矢量
求矢量  和
和  的夹角
的夹角  。
。
解 

 所以
所以 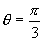
例3 证明:矢量 垂直于矢量
垂直于矢量 。
。
解 

 垂直于向量
垂直于向量 
例4 设  ,求
,求  的模。
的模。
解 

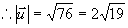
例5 设 若
若  ,则
,则  ?
?
解 
所以 
2.函数  是否方程(**)的通解呢?这要看
是否方程(**)的通解呢?这要看  与
与
 是否独立,如果
是否独立,如果
 ,则
,则

 ,
,
式中只有一个独立常数,显然,此时不是(**)的通解。
下面给出两个函数线性相关、线性无关的概念:
设函数  与
与
 在区间I有定义,且其中之一是另一个的常数倍(即
在区间I有定义,且其中之一是另一个的常数倍(即  ),则称函数
),则称函数
 与
与
 线性相关,否则称为线性无关或线性独立。
线性相关,否则称为线性无关或线性独立。
如:  与
与  相关;
相关; 与
与
 无关;
无关;
 与
与 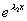 当
当
 时无关。
时无关。
定理2 如果函数  与
与
 是齐次方程(**)的两个线性无关的特解,则
是齐次方程(**)的两个线性无关的特解,则
 (
(  是任意常数)是齐次方程(**)的通解。
是任意常数)是齐次方程(**)的通解。

定理3 设  是二阶非齐次方程(*)的一个特解,
是二阶非齐次方程(*)的一个特解,  是与(*)对应的
是与(*)对应的
齐次方程(**)的通解,则  是二阶非齐次线性方程
是二阶非齐次线性方程
(*)的通解。
定理4 设  与
与
 分别是方程
分别是方程
与 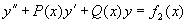 的特解,则
的特解,则
 是方程
是方程  的特解。
的特解。
二阶常系数齐次线性微分方程
形如 
 为常数) (1)
为常数) (1)
或 
 都是常数)的方程称为
都是常数)的方程称为
二阶常系数齐次线性微分方程。
下面求它的通解设  为方程(1)的解,将其代入方程得
为方程(1)的解,将其代入方程得
 (*)
(*)
此称为齐次方程(1)的特征方程,其根叫特征根,记
 称为齐次
方程(1)的特征多项式。显然,如果
称为齐次
方程(1)的特征多项式。显然,如果  是特征方程的根,则函数
是特征方程的根,则函数
 一定是齐次方程(1)的解,下面根据特征方程根的不同情况,讨论齐次方程(1)的通解形式
一定是齐次方程(1)的解,下面根据特征方程根的不同情况,讨论齐次方程(1)的通解形式
(1)特征方程有两个不等的实根 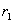 与
与
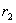
由解的结构知方程(1)的通解为 
(2)特征方程有两个相等的实根 
此时只得到方程(1)的一个解  ,现找出与
,现找出与
 线性无关的另一个解,
线性无关的另一个解,
设  ,将
,将
 代入方程(1)得
代入方程(1)得

即 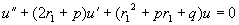
所以  取
取
 得方程(1)的另一解
得方程(1)的另一解  ,
,
方程(1)的通解为 
(3)特征方程有一对共轭复根 
此时,方程(1)的两个解为
 ,
, 
由齐次方程(1)的解的性质(叠加原理)知
 ,
, 
仍为方程(1)的解,且  与
与
 线性无关,
线性无关,
方程(1)的通解为 
综上所述,求二阶齐次常系数线性微分方程的通解的方法是:
(1)写出特征方程,(2)求出特征根,(3)根据特征根的不同情况写出通解。
通解公式:
特征方程  的根 的根
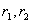 |
通解公式(其中  为任意常数) 为任意常数) |
有两个不等的实根 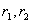 |
 |
有两个相等的实根  |
 |
有一对共轭复根  |
 |
例1 求下列微分方程的通解
(1) 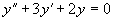
(2) 
(3) 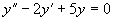
(4) 
解(1)特征方程为 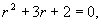
 特征根为
特征根为 
故原微分方程的通解为 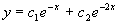
(2)特征方程为 
 特征根为
特征根为 
故原方程的通解为 
(3)特征方程为  ,
,  特征根为
特征根为

故原方程的通解为 
(4)特征方程为  ,特征根为
,特征根为 
故原方程的通解为 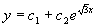
例2 求方程  满足条件
满足条件
 的特解。
的特解。
解 特征方程  ,特征根
,特征根 
所以方程通解为 
代入初始条件  ,
,
 ,
,  ,
,
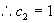
所求特解为 
二阶常系数线性非齐次微分方程的一般形式
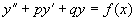 (
( 为常数)
(1)
为常数)
(1)
根据非齐次线性方程解的结构定理(定理3),只要找出其一个特解

和对应的齐次方程
 (2)
(2)
的通解  ,则可得到非齐次方程的通解
,则可得到非齐次方程的通解
 。而齐次方程的通解求法上一
节已介绍,本节主要介绍非齐次方程的特解求法。下面分别介绍
。而齐次方程的通解求法上一
节已介绍,本节主要介绍非齐次方程的特解求法。下面分别介绍  为两种特殊形式时其特解
为两种特殊形式时其特解
 的求法(待定系数法)。
的求法(待定系数法)。

 型
型
其中  是常数,
是常数, 是
是
 的 m 次多项式:
的 m 次多项式:
 。
。
由函数  的形式,可设特解为
的形式,可设特解为
 ,(
,( 是
是  的多项式)
的多项式)
则 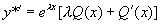 ,
, ,
,
将其代入方程(1)得
 (*)
(*)
即  (
(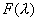 为对应的齐次方程的特征多
项式)
为对应的齐次方程的特征多
项式)
(1)当  不是齐次方程(2)的特征方程的根时,
不是齐次方程(2)的特征方程的根时,
 ,要(*)式两端恒等,
,要(*)式两端恒等, 应是一个 m 次多项式
应是一个 m 次多项式  :
:

将  代入(*)式,比较等号两边
代入(*)式,比较等号两边  同次幂的系数,得到一个以
同次幂的系数,得到一个以
 为未知数的方程组,解出
为未知数的方程组,解出
 ,得到方程(1)的特解
,得到方程(1)的特解  。
。
(2)当  是(2)的特征方程的单根时,
是(2)的特征方程的单根时,
 但
但  ,要(*)式两边相等,则
,要(*)式两边相等,则  应是 m 次多项式,此时可令
应是 m 次多项式,此时可令  ,得到方程(1)的特解
,得到方程(1)的特解  。
。
(3)当  是(2)的特征方程的重根时,
是(2)的特征方程的重根时,
 且
且  ,要(*)式两边恒等,
,要(*)式两边恒等, 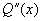 应是 m 次多项式,此时可令
应是 m 次多项式,此时可令  ,得到方程(1)的特解
,得到方程(1)的特解  。
。
综上所述,当  时,非齐次方程(1)的特解求法:
时,非齐次方程(1)的特解求法:
特征方程  的根 的根
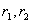 |
特解形式( 是 是  次多项式) 次多项式) |
 不是特征方程的根 不是特征方程的根 |
 |
 是特征方程的单根 是特征方程的单根 |
 |
 是特征方程的重根 是特征方程的重根 |
 |
例1 写出下列方程的特解形式
(1) 
(2) 
(3) 
解(1)对应齐次方程的特征方程为  ,特征根
,特征根  ;
;
 不是特征方程的根,所以,设特解
不是特征方程的根,所以,设特解  。
。
(2)对应齐次方程的特征方程为 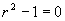 ,特征根
,特征根

 是特征方程的单根,所以,设特解
是特征方程的单根,所以,设特解  。
。
(3)对应齐次方程的特征方程为  ,特征根
,特征根  ;
;
 是特征方程的重根,所以,设特解
是特征方程的重根,所以,设特解  。
。
例2 求方程  的通解。
的通解。
解 对应齐次方程的特征方程为  ,特征根
,特征根  ;
;
齐次方程的通解为  ,
,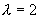 是特征方程的单根,设特解
是特征方程的单根,设特解
 ,
, ,
, ,
, ,
,
特征多项式 
将其代入(*)式 
得 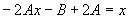 (或将
(或将
 代入原方程也得此结果),
代入原方程也得此结果),
有  ,所以特解为
,所以特解为
 ;故所求通解为
;故所求通解为

例3 求方程  的一个特解。
的一个特解。
解 先求出方程  的特解
的特解
 ,再求出方程
,再求出方程
 的特解
的特解
 ,则原方程的特解为
,则原方程的特解为
 。
。
例4 求方程  满足初始条件
满足初始条件
 的特解。
的特解。
解(1)先求齐次方程的通解:
对应齐次方程的特征方程为 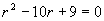 ,其特征根:
,其特征根: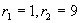
故齐次方程的通解为 
(2)设非齐次方程的特解,并求出待定系数:
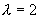 不是特征方程的根,故设非齐次方程的特解:
不是特征方程的根,故设非齐次方程的特解: ,
,
代入原方程,得: ,解得:
,解得: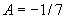 .
.
从而:
(3)写出原方程的通解:所以原方程的通解 

(4)由初始条件求原方程的特解:

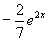 ,把初始条件
,把初始条件  代入
代入
 :
:
得: ,解方程得:
,解方程得:
(5)结论:所以所求特解为: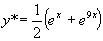


用欧拉公式将  写成复指数形式
写成复指数形式




其中  是
是
 的
的
 次多项式,用
次多项式,用  中
方法先求出方程
中
方法先求出方程 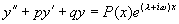 的特解
的特解

 的特解
的特解 
由解的结构定理 4 知,原方程的通解为

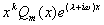




其中  是
是
 的
的
 次多项式,
次多项式, 按
按
 不是或是特征方程的根依次取 0 或 1 。
不是或是特征方程的根依次取 0 或 1 。
由上述推导过程知:如果方程(1)右端 
可设方程的特解为


代入原方程,比较等号两边同类项的系数得一方程组,可确定  中的
系数。
中的
系数。
特殊情况: ,
, 为常数,不同时为零
为常数,不同时为零
(Ⅰ)  不是特征方程的根,设特解
不是特征方程的根,设特解

(Ⅱ)  是特征方程的根,设特解
是特征方程的根,设特解 
 为待定系数。
为待定系数。
例5 写出下列方程的特解形式
(1) 
(2) 
(3) 
解(1)对应齐次方程的特征方程为  ,特征根
,特征根
 ,
,
 不是特征方程的根,设特解
不是特征方程的根,设特解

(2)对应齐次方程的特征方程为  ,特征根
,特征根
 ,
,
 是特征方程的根,设特解
是特征方程的根,设特解 
(3)对应齐次方程的特征方程为  ,特征根
,特征根
 ,
,
 是特征方程的根,设特解
是特征方程的根,设特解 
例6 求方程  的通解。
的通解。
解 对应齐次方程的特征方程为  ,特征根
,特征根
 ,
,
齐次方程的通解为 
下面求特解,将原方程写成


先求出方程  的特解
的特解

因  是特征方程的根,设特解
是特征方程的根,设特解
 ,
,
 ,特征多项式
,特征多项式
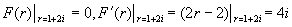 ,将上面结果代入(*)式
,将上面结果代入(*)式
 得
得 
所以特解 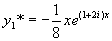 ,
,
显然方程  的特解
的特解
 ,
,
所以原方程的特解为


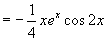
故原方程的通解为 


注 :此方程特解也可这样求,设  ,将
,将
 代入原方程,可得
代入原方程,可得
 。
。
例7 求方程  满足初始条件
满足初始条件
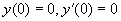 的特解。
的特解。
解 对应齐次方程的特征方程为  ,特征根
,特征根
 ,
,
齐次方程的通解为  ,
,
 不是特征方程的根,设特解
不是特征方程的根,设特解  ,
,


将  代入原方程,化简得
代入原方程,化简得

比较两边同类项的系数,有  ,解得
,解得
 ,
,
所以  ,则原方程的通解为
,则原方程的通解为

而 
将初始条件 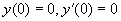 代入上面两式,有
代入上面两式,有
 , 解得
, 解得  ,
,
所以满足初始条件的特解为

3.解微分方程中,遇到取对数时,在不影响微分方程的解的情况下,可以略去绝对值记号。
例3 
解 原式为  分离变量:
分离变量:

两边积分得通解 
例4 求方程 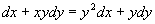 满足初始条件
满足初始条件
 的特解。
的特解。
解 先求通解,原式化为 
分离变量 
两边积分(在对数内略去绝对值记号得)
 即
即 
求得通解为 
代入初始条件  ,
,

所以满足初始条件的特解为 
例5 求方程 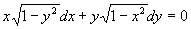 的通解。
的通解。
有些不能分离变量的一阶方程,通过适当的变量置换可以化为可分离变量的方程。
例6 证明:利用变量置换  可将方程
可将方程
 化为变量
化为变量
 与
与
 可分离的方程。
可分离的方程。
证明 :  两边对
两边对  求导得
求导得

 (这是变量已分离的方程)
(这是变量已分离的方程)
例7 求方程  的通解。
的通解。
解 设  ,则
,则

分离变量  ,积分
,积分

所以,通解为 

形如 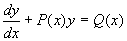 或
或
 (1)
(1)
的方程叫一阶线性微分方程,当  时,
时, (2)
(2)
(2)称为与(1)相应的线性齐次方程,而(1)称为线性非齐次方程。
解法 :(1)先求出线性齐次方程(2)的通解,
分离变量 
两边积分 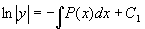
得齐次方程的通解  (
(
 )
)
(2)再用常数变易法来求非齐次线性方程(1)的通解。
设  则
则
 将其代入非齐次方程(1)
将其代入非齐次方程(1)



将  代回得非齐次方程通解
代回得非齐次方程通解
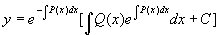 (3)
(3)
注 :将通解公式(3)右边写成两项之和可看出: 一阶线性非齐次方程的通解等于它的一个特解加上对应的齐次方程的通解。
一阶线性微分方程的解法,可用常数变易法,也可直接套用通解公式(3)。
例8 求方程  满足初始条件
满足初始条件
 的特解。
的特解。
解 法一、常数变易法,先求  的通解,
的通解,
分离变量  ,两边积分得
,两边积分得
 ,所以通解为
,所以通解为
 ,
,
令  ,将
,将
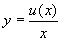 代入原方程
代入原方程
 ,
, 

所以原方程的通解为 
代入初始条件  ,
,

所求特解为 
法二、直接套用通解公式,方程变形为 
其中  ,由通解公式
,由通解公式



代入初始条件后,得特解 
例9 求方程  的通解。
的通解。
解 :原方程为  ,
令
,
令  ,
,
则原方程化为一阶线性方程 
其通解为  。
。
于是原方程的通解为  。
。
例10 求方程 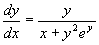 的通解。
的通解。
解 容易看出,这方程既不能分离变量也不是一阶线性方程,但是,如果把  看作
看作
 的函数,
的函数,
 当作自变量,方程化为
当作自变量,方程化为
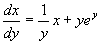 这是一阶线性方程,由通解公式
这是一阶线性方程,由通解公式



例11 求方程  满足初始条件
满足初始条件
 的特解。
的特解。

形如  (
(
 为常数)的方程称为伯努利方程。
为常数)的方程称为伯努利方程。
 时,它是一阶线性方程;
时,它是一阶线性方程; 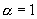 时,它是变量可分离方程。
时,它是变量可分离方程。
当  或1时,方程两边同乘
或1时,方程两边同乘  ,有
,有
 即
即 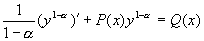
令  ,则伯努利方程化为一阶线性微分方程
,则伯努利方程化为一阶线性微分方程
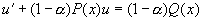
例12 求方程  的通解。
的通解。
解 这是伯努利方程,两边同乘 
 即
即 
令  ,得
,得
 ,由一阶线性微分方程通解公式
,由一阶线性微分方程通解公式




所以,原方程的通解为 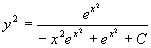
下面再介绍几个微分方程应用的例子。
例13 一平面曲线,其上任一点处的切线夹于两坐标轴之间的那一段切线的长为切点所等分,求曲线的方程。
解 设曲线的方程为  ,
,

 为曲线上任一点(见图8-1),
为曲线上任一点(见图8-1),
由于两坐标轴间切线段被切点所等分,
所以切线与  轴交点为
轴交点为
 ,
,
与  轴交点为
轴交点为
 ,故有
,故有
 ,分离变量,
,分离变量,
两边积分得  ,所求曲线方程为
,所求曲线方程为

例14 设有一质量为  (常数)的物体,从高空以竖直方向上的初速度
(常数)的物体,从高空以竖直方向上的初速度
 开始下落,假定空气的阻力与速度成正比,求物体运动速度与时间的关系。
开始下落,假定空气的阻力与速度成正比,求物体运动速度与时间的关系。
解 取物体下落路径作一坐标轴,正向向下,原点为运动的起点。在运动过程中,物体受到两个力的作用:重力  向下,空气阻力
向下,空气阻力

 向上,由牛顿第二定律得,
向上,由牛顿第二定律得,
 或
或  其中
其中

这是一阶线性方程(也是变量可分离方程),通解为 


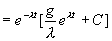

代入初始条件  ,
,

得满足条件的特解是
例15 设  具有连续导数,且满足方程
具有连续导数,且满足方程
 ,求
,求

解 已知  ,方程两边对
,方程两边对
 求导得
求导得

分离变量得  ,两边积分后得
,两边积分后得
 。因
。因
 ,故c=1
,故c=1
因此所求函数 

解法: 逐次积分
例1 求微分方程  的通解。
的通解。
解 两边积分 

再积分得通解 

解法 :令  则
则
 代入方程降阶
代入方程降阶
 这是一阶方程,设通解为
这是一阶方程,设通解为
 即
即
 ,所以,原方程通解为
,所以,原方程通解为

例2 求方程  的通解。
的通解。
解 方程不含y,令 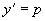 ,故
,故
 ,代入原方程得到
,代入原方程得到
 ,或
,或 
它是p的一阶线性方程,其通解为

再由方程  积分后得到原方程的通解为
积分后得到原方程的通解为
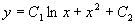
例3 求微分方程  满足初始条件
满足初始条件
 的特解。
的特解。
解 设 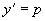 ,故
,故
 ,代入原方程得到
,代入原方程得到
 ,这是变量可分离方程,分离变量,积分
,这是变量可分离方程,分离变量,积分

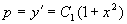 ,再积分得通解
,再积分得通解 
代入初始条件  ,
,

所求特解为 
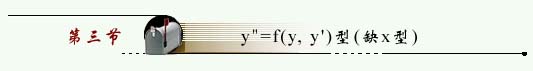
解法 :令  则
则
 代入方程降阶
代入方程降阶
 这是一阶方程,设通解为
这是一阶方程,设通解为
 即
即
 ,所以,原方程的通解为
,所以,原方程的通解为
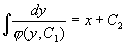
例4 求方程  的通解。
的通解。
解 令  代入原方程得
代入原方程得
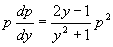 ,
,
当  时,得
时,得
 为原方程的解;
为原方程的解;
当  时,
时,
 ,分离变量后得
,分离变量后得
 ,
,
两边积分后得  即
即
 ,
,
从而得 
分离变量,再两边积分,得原方程所求通解为 
例5 求方程  的通解。
的通解。
2.在求解微分方程时,由于方程的变形,常使某些解不在所求得的通解中。一般说,这种解容易从方程中直接观察出,有时,适当扩大通解中任意常数的取值范围,可把这些解包含进去(如例1)。另一方面,实际问题中求解微分方程的主要目的是寻找满足初始条件的特解,这样的特解大都可以从通解中定出,例外的情况也不难直接从方程得出。所以今后将不再指出这些不属于通解中的解。
1.如果由方程  (*)确定的隐函数
(*)确定的隐函数  是一个微分方程的解(通解),则(*)式叫微分方程的隐式解(隐式通解),如上例。
是一个微分方程的解(通解),则(*)式叫微分方程的隐式解(隐式通解),如上例。
3.复合函数微分法(微分形式的不变性)
设  可微
可微
(1)当u为自变量时,

(2)当  时,
时,


求  的微分
的微分
 时,可先求出
时,可先求出
 再写出微分,也可利用微分法则和微分形式的不变性。
再写出微分,也可利用微分法则和微分形式的不变性。
例1 设 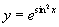 ,求
,求

解 法一 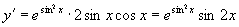

法二 
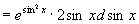


例2 设  ,求
,求

解 法一 

法二 

例3 设  ,求当
,求当
 时的微分。
时的微分。
解 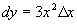

例4 求下列函数的微分
(1)  (2)
(2)  可导
可导
解 (1) 
(2) 
例5 填空
(1)  ,(2)
,(2) 
解 (1)因为  ,即
,即
 填
填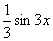 。
。
(2)因为  ,所以填
,所以填
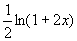

由微分的定义知,当  很小时,有
很小时,有

 ,也即下面的近似计算公式
,也即下面的近似计算公式
 (1)
(1)
或 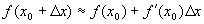 (
(
 很小)
(2)
很小)
(2)
例6 有一批半径为1cm的球,为了提高球面的光洁度,要镀上一层铜,厚度为0.01cm,估计一下每只球需要用多少克铜(铜的比重是  )?
)?
解 设球体积为  ,半径为
,半径为
 ,则
,则
 ,
,
现  ,求体积的对应改变量
,求体积的对应改变量
 ,
,

 ,
,
所以每只球需要铜约为 
例7 求  的近似值。
的近似值。
解 将  化成弧度,
化成弧度,

 ,设
,设
 ,则
,则
 ,
,
取  ,利用公式(2)
,利用公式(2)


在(2)式中令 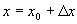 ,则(2)成为
,则(2)成为

此式说明当  在
在
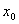 的邻域内可导时,
的邻域内可导时,
 可表示成
可表示成

的线性函数。如果  ,可得近似公式
,可得近似公式
 (
(  很小)
很小)
利用上式可推出书中151页的几个近似公式。如:
 ;
;  ;
;
 ;
;
 。
。
例8 求  的近似值。
的近似值。
解 由于 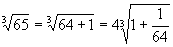 ,
,
 ,利用上面第一式,
,利用上面第一式,


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com