3. 若关于x的方程有四个不相等的实根，则实数m的取值范围为___________。

2. 若对任意实数t，都有，则、由小到大依次为___________。

1. 若复数z满足，则的最大值为___________。

6. 解析：令，

　　 若a>1，两函数图象如下图所示，显然当时，

　　 要使，只需使，综上可知

　　 当时，不等式对恒成立。

　　 若，两函数图象如下图所示，显然当时，不等式恒不成立。

　　 综上可知a的取值范围为(1，2]

二　范例剖析

例1　 设A={x||x|=kx+1},若A∩R₊=φ,A∩R_-≠φ,求实数k的取值范围．

例2 求函数的值域。

例3(2006福建)已知函数

(I)求在区间上的最大值

(II)是否存在实数使得的图象与的图象有且只有三个不同的交点？若存在，求出的取值范围；若不存在，说明理由。

四　巩固训练

5.分析：

4.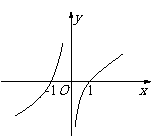 解析：由已知画出y=f(x)的图象可知：

当x∈(-1，0)∪(1，+∞)时f(x)＞0，当x∈(-∞，-1)∪(0，1)时　 f(x)＜0

又x(x-)=(x-)²-≥-＞-1∴f(x(x-))＜0成立，则必有

0＜x(x-)＜1,解之得：＜x＜0或＜x＜

3. 解析：画出的图象可知，有四个交点则；　

2. 解析：分析方程的结构特点，联想椭圆第二定义，可知应把左右两边分别化为两点间的距离和点到直线的距离：，

即时表示椭圆，解得m>5

点评：本题考查椭圆的第二定义，考查数形结合和综合运用解析几何知识分析解题的能力。

1. 解析：因为是二次函数，值域不会是A、B，画出函数的图像(图1)易知，当值域是时，的仁政域是。

点评：本题考查函数的图像、定义域、值域，是高考的一个重点，考题多以小题形式出现。

6、若时，不等式恒成立，则a的取值范围为　　　

二　感悟解答