21．解：(Ⅰ)令，得　　 ①

令，得　　　　 ②

由①，②得 　　为单调函数， ∴．

(Ⅱ)由(Ⅰ)得，

，

，

(Ⅲ)令，

则

∴当时，

　 即

　解得或

21．(本小题满分14分)

已知定义在R上的单调函数，存在实数，使得对于任意实数总有恒成立．

(Ⅰ)求的值；

(Ⅱ)若，且对任意正整数，有，记，，比较与的大小关系；

(Ⅲ)若不等式对任意不小于2的正整数都成立，求的取值范围．

20．解：(1)由得，

　，

由

．

　 (Ⅱ)由于均为负整数，故也是负整数，且，

由得，

，．

(Ⅲ)证明：，

综上所述， ．

20．(本小题满分13分)

已知函数R)，设关于的方程的两实根为，方程的两实根为．

(Ⅰ)若，求的关系式；

(Ⅱ)若均为负整数，且，求的解析式；

　 (Ⅲ)若．

19．解：(Ⅰ)由可知四边形为平行四边形，

，四边形为菱形，

．

(Ⅱ)由已知得， 的坐标分别为，

,

,　 ,

,

，此时．

(Ⅲ)由得， ，

．

19．(本小题满分12分)

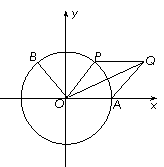如图，是单位圆与轴正半轴的交点，点在单位圆上，，，四边形的面积为．

(Ⅰ)试判断四边形的形状并求其面积；

(Ⅱ)设函数,求

的最大值及对应的的值；

(Ⅲ)设点的坐标为，，在(Ⅱ)的条件下，求．

18．解：设

　　　 连结BD．

　　　 则在中，

　　　 设

　　　 则

　　　 等号成立时

　　　 答：当时，建造这个支架的成本最低．

18．(本小题满分12分)

某建筑的金属支架如图所示，根据要求至少长，为的中点，到的距离比的长小，，已知建筑支架的材料每米的价格一定，问怎样设计的长，可使建造这个支架的成本最低?

17．解: (Ⅰ)

　　　　　 又, 得，

　　　　　 或．

(Ⅱ)

　　　　 与共线,

，

,当时，取最大值为 ，　

由，得，此时．

17．(本小题满分12分)

在平面直角坐标系中，为坐标原点，已知，点

．

(Ⅰ)若且，求向量；

(Ⅱ)若与共线，当时，且取最大值为4时，求．