3．某瓜果基地市场部为指导该基地某种蔬菜的生产和销售，在对历年市场行情和生产情况进行了调查的基础上，对今年这种蔬菜上市后的市场售价和生产成本进行了预测，提供了两个方面的信息，如甲乙两图，注甲乙两图中的每个黑心点所对应的纵坐标分别指相应月份的售价和成本，生产成本6月份最低，甲图的图像是线段，乙图的图像是抛物线。请你根据图像提供的信息说明

(1)　　　 在三月份出售这种蔬菜，每kg的收益是多少元？(收益=售价－成本)

(2)　　　 那个月出售这种蔬菜，每kg的售价最大，说明理由。

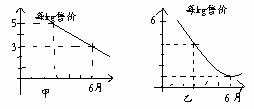
2.某化工材料经销公司购进了一种化工原料共7000kg,购进价格为30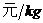,物价部门规定其销售单价不得高于70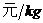,也不得低于30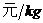,市场调查发现:单价定于70元时,日均销售60kg,单价每降低1元,日均多售出2kg,在销售过程每天还要支出其它费用500元,(不足一天时,按整天计算),设销售单价为x元,日均获利为y元，

(1)　　　 求y关于x的二次函数关系式，并注明x的取值范围。

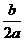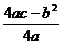(2)　　　 将(1)中所求出的二次函数配方成y=a(x+)²+的形式，写出顶点坐标，画出草图，观察图像，指出单价定为多少时日均获利最多，是多少？

(3)　　　 将这种化工原料全部售出，比较日均获利最多和销售单价最高，这两种销售方式，哪一种获总利最多，多多少？

1.某玩具厂计划生产一种玩具熊猫,每日最高产量为40只且每日产出的产品全部售出,已知生产x只玩具熊猫的成本为R元,售价每只为P(元),且R,P与x的关系式分别为R=500+30x , P=170－2x.

(1)　　　 每日产量为多少时,每日获得的利润为1750元？

(2)　　　 每日产量为多少时,可获得的最大利润？最大利润是多少？

练习

2、　　　　　 能运用图形运动、函数建模、数形结合等数学思想解决实际生活问题和有关二次函数的综合题。

1、　　　　　 熟悉二次函数的各种解析式的适用条件和解题思路，一般地，已知三点选用一般式，已知顶点选用顶点式，已知与x轴两交点选用两根式；

1、已知：在直角坐标平面上，二次函数图像的顶点坐标为C(3，- 4)，在x轴上截得线段AB的长为4.

(1)求这个二次函数解析式；

(2)在y轴上是否存在一点Q，使QA+QC最小？如果存在，求出点D的坐标;如果不存在，请说明理由。

4、　　　　　 经过点A(0，1)，B(1，3),且沿X轴右移2个单位后经过点(1，1).

例2：有一个抛物线形的立交桥拱，它的最大高度为16米，跨度为40米。现要在离跨度中心5米处的两侧各垂直竖立一铁柱支撑拱桥，这两根铁柱应取多长？

例3：平移二次函数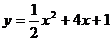的图像，使它经过A(-3,6)和B(-1,0)。

(1)　　 求这个抛物线的解析式；

(2)　　 点C为此抛物线与x轴的另一个交点，点P为顶点，问在x轴上是否存在点D，使△DCP与△ABC相似？若存在，求出点D的坐标；若不存在，请说明理由。

思考题：关于x的二次函数y = x²-2mx-m的图像与x轴交于A(x₁,0),

B(x₂,0)两点，且x₂> 0> x₁,与y轴交于C点，且∠BAC= ∠BCO。

(1)　　 求这个二次函数解析式；

(2)　　 以点D(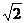 ，0)为圆心作⊙D，与y轴相切于点O，过抛物线上一点E(x₃,t)(t >0,x₃<0)作x轴的平行线与⊙D交于F、G两点，与抛物线交于另一点H。问：是否存在实数t，使得EF+GH=FG？若存在，求出t的值；若不存在，请说明理由。

3、　　　　　 顶点坐标为(2，1)，且经过点(1，2)；

2、　　　　　 经过A(-1，0)，B(2，0)，C(4，-10)三点；