3．抛物线y=a(x-h)²+k的图象性质

当a>0时，抛物线的开口向上，

　x＜h时，y随x的增大而减小。

　　　　　 x＞h时，y随x的增大而增大。

x=h时，函数有最小值是k。

当a<0时，抛物线的开口向下，

　x＜h时，y随x的增大而增大。

　　　　 　x＞h时，y随x的增大而减小。

　　　　 　x=h时，函数有最大值是k。

y=ax²,y=ax²+k ,y=a(x-h)² ,y=a(x-h)²+k四者之间的关系，如图13-7所示：

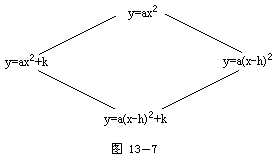
注意：基本形式中的符号，特别是h．

例题与练习：

例1: 已知抛物线y=4(x-3)²-16　

(1)写出它的开口方向，对称轴，顶点坐标。

(2)写出函数的增减性和函数的最值。

例2：已知函数y=x²+2x-2,求出图像的顶点坐标、对称轴。

归纳：利用配方法可以将二次函数y=ax²+bx+c变形为y=a(x-h)²+k，再求出顶点坐标，对称轴。

例3：用配方法求抛物线y=x²-6x+21的对称轴，顶点坐标。

(注意：配方时不能除以)

练习：用配方法将下列函数变形为y=a(x-h)²+k形式，指出它们的对称轴，顶点坐标。

(1)　 y=x²+2x+　　　　　　　　 (2) y=-2x²+8x

(3)　 y=－x²+4x+5　　　 　　　　　(4) y=x²-2x+

总结：

二次函数y=ax²+bx+c通过配方变形成y=a(x-h)²+k的形式。

2.抛物线y=a(x-h)²+k的图象平移

函数y=a(x-h)²+k的图象是将函数y=ax²的图象先向上或向下平移|k|个单位，再向左或右平移|h|个单位得到的。

(或函数y=a(x-h)²+k的图象是将函数y=ax²的图象先向左或右平移|h|个单位，再向上或向下平移|k|个单位得到的。)

(移动规律可以简单记作：左加右减，上加下减)

1．抛物线y=a(x-h)²+k的图象

　　　　　 抛物线y=a(x-h)²+k与抛物线y=ax²的形状相同，开口方向相同，

对称轴是直线x=h；顶点坐标为(h，k)

2．填表：

函数	开口方向	顶点坐标	对称轴	增减性
y= －x2
y=3x2－2
y=2(x+1)2
y= －(x－1)2

新课：讨论形如y=a(x-h)²+k的二次函数的图像．

整体感知: 利用计算机课件演示二次函数 y=0.5x²,y=0.5x²+1,y=0.5(x+1)²的图象，并指出它们的开口方向，对称轴及顶点坐标．

通过对这几个图象的观察能更全面、更直观地看到图形之间的平移变化，

　　 问题：在坐标系中如何画出函数y=0.5(x+2)²-3的图像？(猜想这个图像的大致形状和位置)

(1)指出抛物线的开口方向、对称轴、顶点坐标及增减性、最值。

看下列图表：

(2)我们已知抛物线的开口方向是由二次函数y=a(x-h)²+k中的a的值决定的，你能通过上表中的特征，试着总结出抛物线的对称轴和顶点坐标是由什么决定的吗？

这个问题由于是本节课的重点问题，而且不是很容易说清楚，可由学生进行广泛的讨论，先得出对称轴的表示方法，再得出顶点坐标．若学生在讨论时没有头绪，教师可适当引导，让学生把这四个函数都改写

_[来源:]

式子中加以观察，分析，得出结论：(板书)

　 归纳：

复习：

1．提问：前几节课，我们都学习了形如什么样的二次函数的图象？

答：形如y=ax²，y=ax²+k和y=a(x-h)²．

2．教学难点：确定形如y=a(x-h)²+k的二次函数的顶点坐标和对称轴．

1．教学重点：会画形如y=a(x-h)²+k的二次函数的图象，并能指出图象的开口方向、对称轴及顶点坐标．

(三)德育渗透点：向学生渗透事物间互相联系，以及运动、变化的辩证唯物主义思想．

(二)能力训练点：1．继续培养学生的作图能力；2．培养学生的观察、分析、归纳、总结的能力；3．向学生进行数形结合的数学思想方法的教育．

(一)知识教学点：1．使学生掌握抛物线y=a(x-h)²+k的对称轴与顶点坐标．2．使学生会用配方法将二次函数y=ax²+bx+c 变形为y=a(x-h)²+k形式。