2、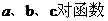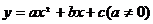的性质与图象有哪些影响？

1、二次函数的定义及图象的形状是怎样的？

3、在教学中渗透美的教育，渗透数形结合的思想.

重点：理解二次函数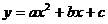的性质，

难点：二次函数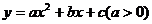的增区间和减区间。

[概念探究]

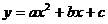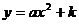2、　 通过探索让学生经历二次函数性质探究的过程，理解二次函数的性质及它与函数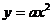的关系。

1、　 让学生学会画函数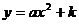的图象，并能通过图象和解析式，正确地说出开口方向，对称轴以及顶点坐标，图象性质.

2.2.2 二次函数的性质与图象 教案

[教学目标]

3、当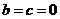时，二次函数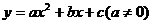变为___________,它的图像和性质特征为：(1)顶点坐标________,奇偶性为_______,图形关于_______对称；

(2)当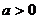时，抛物线的开口______,在_________上是增函数，在­­­­­­­­­­­­­­­­­­­_________上是减函数，当x=_____有最小值_______；当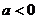时，抛物线的开口_______,在_________上是增函数，在­­­­­­­­­­­­­­­­____________上是减函数，当x=______有最大值_______.

(3) 当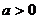时,抛物线在x轴的______，开口向上并随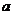的增大逐渐______；当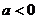时，抛物线在x轴的______，开口向下并随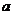的增大逐渐______；

[例题解析]

例1、求函数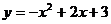的顶点坐标，对称轴以及函数的单调区间.

例2、求函数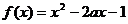在区间[0，2]上的最小值

例3、已知函数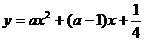的图像恒在x轴上方，求实数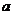的取值范围

2、函数_____________________叫二次函数，它的定义域是_________________.

1、二次函数的定义及图象的形状是怎样的？