20、(1)由f (x)是R上的奇函数得

(2)任取 ，且 ，

则

∵0< ,∴

∴

∴f (x)在(0，+∞)上是增函数

(3)由y= f (x)= 1 -

故值域为(-1,1)

∴函数 的单调减区间为

(3)法一：

法二：

18、解：由

∵0<A<π，0<B<π，∴-π<A-B<π

∴ 或

由 =

∵0<A<π，0<B<π，0 <A+B<π

∴ 或

(1)　　 若 ， ，则 ，舍去；

∴NK∥AM，NK=AM

∴四边形AMNK为平行四边形，MN∥AK

MN 面PAD，AK 面PAD

∴MN∥平面PAD

(2)∵PA⊥面ABCD，∴PA⊥CD，PA⊥AD

又CD⊥AD，AD∩PA=A

∴CD⊥面PAD，AK 面PAD

∴CD⊥AK；

在Rt△PAD中，PA=AD，K为PD中点

∴AK⊥PD，PD∩CD=D

∴AK⊥面PCD，又MN∥AK

∴MN ⊥面PCD，MN 面PMC

∴平面PMC⊥平面PCD

17、解：由

(1)原式=

(2) ，

∵ ，

∴ ，

∴ =

22、(本题14分)设函数，

(1)若当时，取得极值，求的值，并求出的单调区间；

(2)若存在极值，求的取值范围；

(3)若a为任意实数，试求出的最小值的表达式.

21、(本题12分)已知函数f (x)=4sin²(+x)-2cos2x-1(x∈R).

(1)求的最小正周期、最大值及最小值；

(2)求函数的单调减区间.

(3)问f (x)的图象经过怎样的变换才能得到的图象？

20、(本题12分)已知函数f (x)= a-是R上的奇函数．

(1)求a的值；

(2)证明：f (x)在(0，+∞)上是增函数；

(3)求该函数的值域．

19、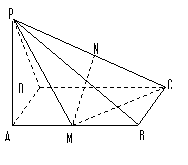(本题12分)四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，M、N分别是AB、PC的中点，PA＝AD＝a. (1)求证：MN∥平面PAD； (2)求证：平面PMC⊥平面PCD.

18、(本题12分)已知在△ABC中，，=，试求出.

17、(本题12分)已知，.[

(1)求的值；

(2)求的值.

16、 给出下列命题：

①存在实数成立；

②存在实数成立；

③函数是偶函数；

④方程是函数的图象的一条对称轴的方程；

⑤若是第一象限角，则．

其中正确的命题的序号是　　　　　　 (注：把你认为正确的命题的序号都填上)．