
BAACB BDDAC
21.(本小题满分14分)
已知函数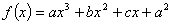 的单调递减区间是
的单调递减区间是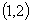 ,且满足
,且满足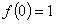 .
.
(Ⅰ)求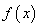 的解析式;
的解析式;
(Ⅱ)对任意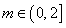 , 关于
, 关于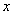 的不等式
的不等式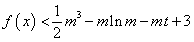 在
在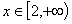 上有解,求实数
上有解,求实数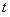 的取值范围.
的取值范围.
厦门六中2009-2010学年高三上期中考试
数学(理科)试题 评分标准
20.(本小题满分14分)
已知数列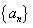 的前
的前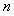 项和
项和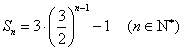 ,数列
,数列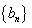 满足:
满足:
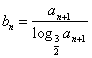
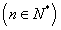 . (1)试求
. (1)试求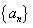 的通项公式,并说明
的通项公式,并说明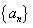 是否为等比数列;
是否为等比数列;
(2)求数列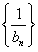 的前n项和
的前n项和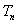 ; (3)求
; (3)求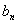 的最小值.
的最小值.
19.(本小题满分13分)
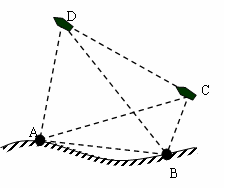 某航模兴趣小组的同学,为了测定在湖面上航模航行的速度,采用如下办法:在岸边设置两个观察点A、B ,且 AB = 80 米,当航模在 C处时,测得 ∠ABC=105°和 ∠BAC=30°,经过20 秒后,航模直线航行到 D 处,测得 ∠BAD=90°和 ∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)
某航模兴趣小组的同学,为了测定在湖面上航模航行的速度,采用如下办法:在岸边设置两个观察点A、B ,且 AB = 80 米,当航模在 C处时,测得 ∠ABC=105°和 ∠BAC=30°,经过20 秒后,航模直线航行到 D 处,测得 ∠BAD=90°和 ∠ABD=45°.请你根据以上条件求出航模的速度.(答案保留根号)
18.(本小题满分13分)
已知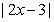 ≤1的解集为
≤1的解集为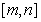
(1)解不等式: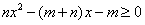 ;
;
(2 )若关于x的不等式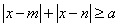 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)若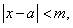 求证:
求证: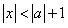 .
.
17.(本小题满分13分)
厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品。
(1)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验。求至少有1件是合格品的概率;
(2)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收。求该商家可能检验出不合格产品数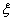 的分布列及期望
的分布列及期望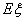 ,并求该商家拒收这批产品的概率。
,并求该商家拒收这批产品的概率。
16.(本小题满分13分)
已知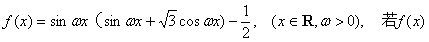 的
的
最小正周期为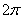 。
。
(I)求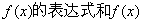 的单调递增区间;
的单调递增区间;
(II)求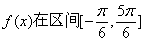 的最大值和最小值。
的最大值和最小值。
15.已知函数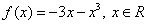 ,若
,若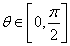 时,不等式
时,不等式
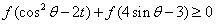 恒成立,则实数t的取值范围是 ★★
恒成立,则实数t的取值范围是 ★★
14.等比数列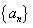 中,
中,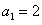 ,前
,前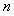 项和为
项和为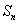 ,若数列
,若数列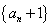 也是等比数列, 则
也是等比数列, 则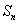 等于★★
等于★★
13.在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为 ★★
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com