
5、答:(3);
解析:新背景下的信息转换问题,需要认真分析对应关系,在对应关系下求出原象,如对于第一个接受信息,依据对应关系可知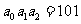 ,求得
,求得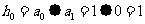 ,同理求得
,同理求得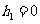 ,故(1)正确;对于(3),若原信息为011,则接收信应为10110。
,故(1)正确;对于(3),若原信息为011,则接收信应为10110。
4、答:①;
解析:演绎推理是从一般性原理出发,推出某个特殊情况下的结论,三段论是演绎推理的一般形式,包括大前提、小前提、结论三部分。这里②③可推出①,其中②是大前提,③是小前提,①是结论。
3、答: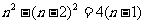 ;
;
解析:归纳推理是依据部分对象或有限的事实,概括出一般性,即从部分到整体,从个性到一般,这里每个等式左边是两个整数的平方差。
2、答:R(S1+S2+S3+S4)
解析:比较两个对象,三边对四面,面积对体积,内切圆对内切球,三边长对四个面的面积,由S=r (a+b+c)等式两边的量,类比对应到体积、系数、半径R、S1+S2+S3+S4
1、答:①②;
解析:类比是两个对象具有某些相似特征,由其中一个对象的某些已知特征,推出另一个对象也具有这些特征的推理,解题时从观察比较入手,根据特征联想类推,从而猜测出新的结论,猜测是否正确需要证明,类比是合情推理的一种,本题中①是由实数集上的关系类比到复数范围上,②是复数上的关系类比到无理数集,结论都正确。
7、某同学准备用反证法证明如下一个问题:函数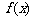 在
在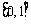 上有意义,且
上有意义,且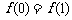 ,如果对于不同的
,如果对于不同的 ,都有
,都有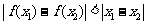 ,求证:
,求证: 。那么他的反设应该是___________.
。那么他的反设应该是___________.
二 感悟解答
6、有一道解三角形的题目,因纸张破损有一个条件模糊不清,具体如下:“在△ABC中,已知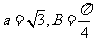 , .求角A.”经推断,破损处的条件为三角形一边的长度,且答案提示
, .求角A.”经推断,破损处的条件为三角形一边的长度,且答案提示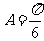 .试在横线上将条件补充完整.
.试在横线上将条件补充完整.
考点3、反证法
5、为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为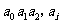
 (
(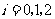 ),传输信息为
),传输信息为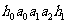 ,其中
,其中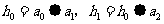 ,
, 运算规则为:
运算规则为: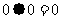 ,
, ,
,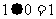 ,
,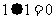 ,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列三个接收信息:(1)11010(2)01100(3)10111,一定有误的是 (填序号)
,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列三个接收信息:(1)11010(2)01100(3)10111,一定有误的是 (填序号)
4、已知①正方形的对角相等;②平行四边形的对角相等;③正方形是平行四边形.根据三段论推理得到一个结论,则这个结论的序号是 .
考点2、分析法和综合法
3、观察下列各式9-1=8,16-4=12,25-9=16,36-16=20…,这些等式反映了正整数间的某种规律,设n表示正整数,用关于n的等式表示为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com