1、下列各组加点字的注音正确的一组是

A．请帖(tiè)　 　　劝谏(jiàn)　　 　肩胛骨(jiǎ)　　 　 面面相觑(xū)

B．殉情(xùn)　　　　 债券(juàn)　　 　门诊室(zhěn)　 　 纨绔子弟(kuā)

C．迤逦(yǐ)　　 　　 　　伺侯(cì)　　 　 　劳什子(shí)　　 　 顿开茅塞(sè)

D．艄公(shāo)　 　　 　　惊骇(hài)　　 　 　执著狂(zhuó)　 　 疏不间亲(jiān)

2．教学中的预期效果分析

本节课我采用现代化的教学手段进行教学，运用已有的知识体系，创造性的使用教材，一根红线贯穿始终,使学生在自主学习与教师引导相结合的教学实践中,从“懂”到“会”到“悟”，体会钻研的意识，品尝成功的喜悦，从而使学生在积极活跃的思维过程中，数学能力和数学素养得到提高．

1．教学方法

　 为了激发学生学习的主体意识，面向全体学生，使学生在获取知识的同时，各方面的能力得到进一步的培养．根据本节课的内容特点，本节课采用启发探究、讲练结合，分组讨论等教学方法，着重于培养学生分析、解决问题的能力以及良好的学习品质．

(1)由于高二的学生已具备一定的空间想象，但对把空间的问题转化为数学的问题的能力有所欠缺，因此在创设情境中安排了实际背景材料--奥运火炬在南昌的传递，对学生进行爱国主义教育，通过动画演示来引出新知，使学生直观的体验空间中两点间的距离和空间两条直线所成的角，目的有以下几点：①通过学生身边的实例，激发学生的学习兴趣，变枯燥的数学为有趣的数学;②使学生感悟到数学就在身边，提高“用数学”的意识;③使学生经历从现实生活中抽象出数学“模型”过程，培养“建模”意识.

(2)由于本节课的重点是夹角和距离公式，而关键在于如何找坐标，学生容易了解，因此在例题的讲解上，充分的发挥学生的主观能动性，尽可能的由他们说出点或向量的坐标,激发学生参与的热情.

(3)由于高二的学生具备一定的学习能力，但在探究问题的内部联系和内在发展上还有所欠缺，为此在例1的基础上设置变式训练,首先将课本中的中点坐标以及求夹角的例题设计到变式训练中给学生以示范,再安排学生在以上的基础上自己编题,目的:①始终以例1为主线,贯穿下来②起到培养学生的合作精神以及对掌握知识的相互补充作用,同时激发学生的学习积极性,让学生真正参与进来,真正的自主的学习.并通过投影仪充分展示学生的成果,在师生双边活动的过程中养成反思意识和提高有条理的表达能力，促进学生全面和谐地发展.

　　 将课本中求空间上到两点距离相等的点的轨迹问题设计到拓展提高当中,引发学生的兴趣,将整堂课推向高潮.

(4)利用程序框图帮助总结求空间两点间的距离与两条直线所成角的步骤.

(5)为适应不同水平的学生, 作业层次有所不同,给例1设计了一问留给学生思考,使得整堂课一根红线贯穿始终.

在人们生活的空间中存在着大量的图形，夹角和距离在现实生活中随处可见,同时它们又是立体几何中的重要问题, 由于高二的学生已具备一定的空间想象，但对把空间的问题转化为数学的问题的能力有所欠缺，而本节课的学习使学生经历对从生活中如何抽象出数学模型的过程，从而有助于培养学生分析问题、解决问题的能力.

本节课是在已完成了“平面向量的数量积公式、夹角公式，空间向量的坐标表示，空间向量的数量积”等内容的教学以后进行的，它研究的是空间中夹角和距离公式,是空间向量在立体几何中的简单应用,是后面学习夹角和距离的基础,同时也肩负着学生用向量法处理立体几何问题，把对空间图形的研究从“定性推理”转化为“定量计算”的任务, 因此本节课的教学内容起着承前启后的作用.这节课的教学，为向量在数学和物理上的综合运用奠定了基础.

本节课是人教版第九章第六节空间向量的坐标运算之夹角和距离公式的第一课时,它是在学生学习了空间向量的坐标表示，空间向量的数量积的基础上进一步学习的知识内容, 沟通了代数与几何的关系，体现了向量的工具性、应用性，渗透了转化、数形结合等数学思想.同时它也是数学建模中很典型的一堂课，是数学研究过程的一个缩影.

这节课希望达到以下教学目标:

三维目标：

知识与技能：　　　　 ⒈使学生知道如何建立空间直角坐标系，掌握向量的长度公式、

夹角公式、两点间距离公式、中点坐标公式，并会用这些公式

解决有关问题；

⒉使学生经历对从生活中如何抽象出数学模型的过程，从而提高分析问题、解决问题的能力.

过程与方法：　　　 　　通过采用启发探究、讲练结合、分组讨论等教学方法使学生在积极活跃的思维过程中，从“懂”到“会”到“悟”.

情感、态度和价值观：⒈通过自主探究与合作交流的教学环节的设置，激发学生的学习热情和求知欲，充分体现学生的主体地位；

　　　　　　　　　 ⒉通过数形结合的思想和方法的应用，让学生感受和体会数学的魅力，培养学生“做数学”的习惯和热情.

22．(本小题满分12分)

　　 已知函数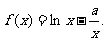

　 (I)若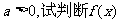在定义域内的单调性；

　 (II)若的值；

　 (III)若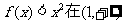上恒成立，求a的取值范围。

21．(本小题满分12分)

　　 已知函数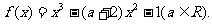

　 (1)若函数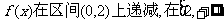上递增，求a的值；

　 (2)在(1)的条件下是否存在实数m，使得函数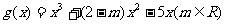的图像与函数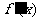的图象恰好有三个不同的交点，若存在，请求出实数m的取值范围；若不存在，请说明理由；

　 (3)当图像上任意一点的切线的倾斜角为，若给定常数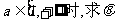的取值范围。

20．(本小题满分12分)

　　 已知函数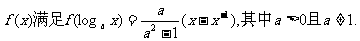

　 (1)求函数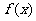的解析式，并指出其单调性；

　 (2)函数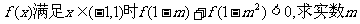的取值集合；

　 (3)当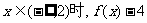的值恰为负数，求a的取值范围。

19．(本小题满分12分)

　　 已知函数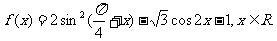

　 (1)若函数的值；

　 (2)设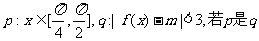的充分条件，求实数m的取值范围。