配方法、待定系数法、换元法是几种常用的数学基本方法.这些方法是数学思想的具体体现,是解决问题的手段,它不仅有明确的内涵,而且具有可操作性,有实施的步骤和作法.

配方法是对数学式子进行一种定向的变形技巧,由于这种配成“完全平方”的恒等变形,使问题的结构发生了转化,从中可找到已知与未知之间的联系,促成问题的解决.

待定系数法的实质是方程的思想,这个方法是将待定的未知数与已知数统一在方程关系中,从而通过解方程(或方程组)求得未知数.

换元法是一种变量代换,它是用一种变数形式去取代另一种变数形式,从而使问题得到简化,换元的实质是转化.

5、解:(1)在小车朝正x方向滑行的过程中,第(n-1)个沙袋扔到车上后的车速为V_n-1,第n个沙袋扔到车上后的车速为V_n,由动量守恒定律有 　　　　[M+(n-1)m]V_n-12nmV_n-1=(M+mn)V_n 　　　　V_n=［M-(n-1)m]V_n-1÷(M+mn)　　① 　小车反向运动的条件是：V_n-1>0,V_n<0,即 　　　　M-nm>0　　　　② 　　　　M-(n+1)m<0　　　 ③ 　代入数字,得：n＜M/m=48/14　　n＞(M/m)-1=34/14 　n应为整数,故n=3,即车上堆积3个沙袋后车就反向滑行、 　(2)车自反向滑行直到接近x<0一侧第1人所在位置时,车速保持不变,而车的质量为M+3m、若在朝负x方向滑行过程中，第(n-1)个沙袋扔到车上后车速为V_n-1′,第n个沙袋扔到车上后车速为V_n′，现取在图中向左的方向(负x方向)为速度V_n′、V_n-1′的正方向,则由动量守恒定律有车不再向左滑行的条件是 　　　　 [M+3m+(n-1)m′]V_n-1′－2nm′V_n-1′=(M+3m+nm′)V_n′ 　　　　　　V_n′={[M+3m－(n-1)m′]V_n-1′}÷(M+3m+nm′)　　④ 　　　　　　　　V_n-1′>0,V_n′≤0 　　　　　　即　M+3m-nm′>0　　　⑤ 　　　　　　 　M+3m-(n+1)m′≤0　 ⑥ 　　　　　　或：n＜(M+3m)÷m′=　9 　　　　　　　n＞(M+3m)÷m′－1　=　8 　　　　　　　　8≤n≤9 　n=8时,车停止滑行,即在x<0一侧第8个沙袋扔到车上后车就停住、故车上最终共有大小沙袋3+8=11个 评分标准:全题12分、第(1)问4分:求得①式给2分,正确分析车反向滑行条件并求得反向时车上沙袋数再给2分、(若未求得①式,但求得第1个沙袋扔到车上后的车速,正确的也给2分。通过逐次计算沙袋扔到车上后的车速,并求得车开始反向滑行时车上沙袋数,也再给2分、) 　第(2)问8分:求得④式给3分,⑤式给1分,⑥式给2分。求得⑦式给1分。得到最后结果再给1分。(若未列出⑤、⑥两式,但能正确分析并得到左侧n=8的结论,也可给上述⑤、⑥、⑦式对应的4分、)

6、设物块质量为m，加速度为a，物块受力情况如下图所示，
　　mgsinθ－f＝ma，
　　N－mgcosθ＝0，
　　f＝μN，
　　解得　　 a＝gsinθ－μgcosθ，
　　由　s=at2/2
　　。

　　
7、设第一次滑块离开时木板速度为v，由系统的动量守恒，有
　　mv0＝mv0/2+Mv，
　　设滑块与木板间摩擦力为f，木板长L，滑行距离s，如右图，由动能定理
　　
　　对木板　　fs＝Mv2/2，
　　对滑块　　
　　　　　，
　　当板固定时　fL＝(Mv02－Mv2)/2，
　　解得
　　　　　。
8、解:物块与钢板碰撞时的速度 
　　　　　　　　　　　　　　①
　设v1表示质量为m的物块与钢板碰撞后一起开始向下运动的速度，因碰撞时间极短，动量守恒， 
　　mv0＝2mv1　　　　　　　　　　　　　② 
　刚碰完时弹簧的弹性势能为EP。当它们一起回到O点时，弹簧无形变，弹性势能为零，根据题给条件，这时物块与钢板的速度为零，由机械能守恒，
　　　　　　　　　　　　③ 
　设v2表示质量为2m的物块与钢板碰撞后开始一起向下运动的速度，
　则有 2mv0＝3mv2 　　　　　　　　　　　　④ 
　仍继续向上运动，设此时速度为v，
　则有 　　　　　　　　⑤ 
　在以上两种情况中，弹簧的初始压缩量都是x0，
　故有 　　　　　　　　　　　　　⑥ 
　当质量为2m的物块与钢板一起回到O点时，弹簧的弹力为零，物块与钢板只受到重力作用，加速度为g。一过O点，钢板受到弹簧向下的拉力作用，加速度大于g。由于物块与钢板不粘连，物块不可能受到钢板的拉力，其加速度仍为g。故在O点物块与钢板分离，分离后,物块以速度v竖直上升，则由以上各式解得，物块向上运动所到最高点与O点的距离为
　　　　l＝v 2/(2g)＝(1/2)x0　　　　　　　　　 ⑦ 
评分标准:本题12分。 ①、②、③、④式各1分，⑤式2分，⑥式3分，得出⑦式再给3分。 

9、解：设抛出点的高度为h，第一次平抛的水平射程

　　 为x，则有　 x2+h2=L2　 ①

　　 由平抛运动规律得知，当初速增大到2倍，其水平

　　 射程也增大到2x，可得

　　　　　　　　 (2x)2+h2=(L)2　 ②

　　 由①、②解得　 h=L/

　　 设该星球上的重力加速度为g，由平抛运动的规律，

　　 得　 h=gt2/2 

　　由万有引力定律与牛顿第二定律，得　 GMm/R2=mg

　　 式中m为小球的质量，联立以上各式，解得

　　　　 M=2LR2/(3Gt2)

10、解：(1)A与B刚发生第一次碰撞后，A停下不动，B 以初速v0向右运动。由于摩擦，B向右作匀减速运动，而C向右作匀加速运动，两者速率逐渐接近。设B、C达到相同速度v1时B移动的路程为s1。设A、B、C质量皆为m，由动量守恒定律，得

　　　 mv0=2mv1　　　　　　　　　　 ①

　　 由功能关系，得

　　　 μmgs1=2mv02/2-mv12/2　　　 ②

　　 由①得　 v1=v0/2

　　 代入②式，得　 s1=3v02/(8μg)

　　 根据条件　 v0<，得

　　　 s1<3l/4 ③ 可见，在B、C达到相同速度v1时，B尚未与A发生第二次碰撞，B与C一起将以v1向右匀速运动一段距离(l-s1)后才与A发生第二次碰撞。设C的速度从零变到v1的过程中，C的路程为s2。由功能关系，得

　　　 μmgs2=mv12/2　　　　　　　 ④

　　 解得　 s2=v02/(8μg)

　　 因此在第一次到第二次碰撞间C的路程为

　　　 s=s2+l-s1=l-v02/(4μg)　　　　 ⑤

　　　　 (2)由上面讨论可知，在刚要发生第二次碰撞时，A静止，B、C的速度均为v1。刚碰撞后，B静止，A、C的速度均为v1。由于摩擦，B将加速，C将减速，直至达到相同速度v2。由动量守恒定律，得

　　　 mv1=2mv2　　　　　　　　　　 ⑥

　　 解得　 v2=v1/2=v0/4

　　 因A的速度v1大于B的速度v2，故第三次碰撞发生在A的左壁。刚碰撞后，A的速度变为v2，B的速度变 为v1，C的速度仍为v2。由于摩擦，B减速，C加速，直至达到相同速度v3。由动量守恒定律，得

　　　 mv1+mv2=2mv3　　　　　　　　 ⑦

　　 解得　 v3=3v0/8　 

　　故刚要发生第四次碰撞时，A、B、C的速度分别为

　　 vA=v2=v0/4　　　　　　　　　 ⑧

　　　 vB=vC=v3=3v0/8　　　　　　　 ⑨

4、由匀加速运动的公式v²＝v₀²+2as，得物块沿斜面下滑的加速度为： 　　　　a＝v²/(2s)＝1、4²/(2×1、4)＝0、7m/s²　① 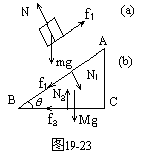　　　　　　　　 　　　　　　　　 　由于a<gsinθ＝5米/秒，可知物块受到摩擦力作用。分析物块受力，它受三个力，如图19-23所示，对于沿斜面的方向和垂直于斜面的方向,由牛顿定律,有： 　　　　mgsinθ-f₁＝ma　② 　　　　mgcosθ-N₁＝0　 ③ 　分析木楔受力,它受五个力作用,如图19-23所示,对于水平方向,由牛顿定律,有： 　　　　f₂+f₁cosθ-N₁sinθ＝0,④ 　由此可解得地面作用于木楔的摩擦力： 　　　　f₂＝N₁sinθ－f₁cosθ＝mgcosθsinθ－(mgsinθ－ma)cosθ 　　　　　　　　　＝macosθ＝1×0、7×(2/3)＝0、61N 　此力的方向与图中所设的一致(由C指向B的方向) 　　　　　　　　　

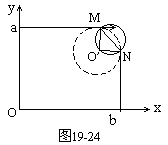
2、解法一: 　秤的结构如图所示，秤钩B到提钮的距离为d，零刻度(即定盘星)A到提钮的距离为l₀，满刻度D到提钮的距离为l，秤杆和秤钩所受的重力为P，秤水平时，P对提钮的力臂为d₀，设秤砣的质量为m，杆秤的最大秤量为M。 　　　当空秤平衡时，有 　　　mgl₀=Pd₀　　 　　　　① 　　　当满秤量平衡时，有 　　　Mgd=Pd₀+mgl　　　　　② 　　　解①、②两式得 　　　m＝(Md)/(l₀+l)　　　　③ 　从秤杆上读出最大秤量M，用直尺测出d和从A点到D点的距离(l₀+ l)，代入上式即可求得m。 　评分标准:全题6分。①、②两式都正确给3分，只有一式正确给1分;求得③式再给1分;说出用直尺测量d( l₀+ l)两个量给2分，缺少其中任何一个量都不给这2分;说分别测量d、l₀、l的也给这2分，但缺少其中任何一个量都不给这2分。把定盘星放在提钮的另一侧，正确的，同样给分。 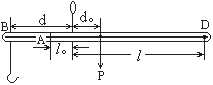　　　　　　　 　解法二: 　秤的结构如图所示。设秤钩B到提钮的距离为d，秤杆和秤钩所受的重力为P。秤水平时，P对提钮的力臂为d₀，秤砣的质量为m。 　设想先把秤砣挂在秤杆读数为M₁处，该处到提钮的距离为l₁，平衡时有: 　　　　　　M₁gd=Pd₀+mgl₁　　　　　　　 ① 　再把秤砣挂在秤杆的读数为M₂处，该处到提钮的距离为l₂，平衡时有: 　　　　　　M₂gd=Pd₀+mgl₂　　 　　　　　② 　解①、②两式得 　　　　　m＝(M₂－M₁)d/(l₂－l₁)　　　　　③ 　从秤杆上读出M₁、M₂，用直尺测得d和从M₁处到M₂处的距离l₂-l₁，代入上式即得m。 　评分标准:与解法一相同。 　　　　　 　解法三: 　秤的结构如图所示，秤钩B到提钮的距离为d，A是零刻度(即定盘星)，D是满刻度。设秤砣的质量为m。当把秤砣挂放在零刻度上，秤平衡时秤钩是空的。若把秤砣从A点移到D点，对提钮增加的力矩为mgl，l为AD间的距离，则在秤钩上挂一质量为M的物体后，秤又平衡。这表示重物对提钮增加的力矩Mgd与mgl大小相等，即 　　　　　　Mgd=mgl　　　　　　　 ① 　解得：　　　　m＝(Md)/l 　从秤上读出最大秤量M，用直尺量出d和l，代入上式即求出m。 　评分标准:全题6分。在分析正确，说理清楚的前提下，直接得到①式给4分;说出用直尺测量l、d两个量给2分，缺少其中任何一个量，不给这2分。 　　　　　 3、解法一: 　设作用于平板车的水平恒力为F，物块与车板间的摩擦力为f，自车启动至物块开始离开车板经历的时间为t，物块开始离开车板时的速度为v，车的速度为V，则有 　　　　　　　(F-f)s₀=(1/2)MV²　　 　　　　　 　　① 　　　　　　f(s₀－b)＝(1/2)mv²　　　　　②　 　　　　　　　(F-f)t=MV③ 　　　　 ft=mv　　　　　　　　　④ 　　　　　　　f=μmg　　　　　　　　⑤ 　由①、②得 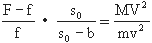　　　　　　　　　　　　⑥ 　由③、④式得 　　　　　(F－f)/f＝(MV)/(mv)　　　　　　⑦ 　由②、⑤式得 　　　　 　　　　　=2米/秒 　由⑥、⑦式得 　　　　V＝s₀/(s₀－b)v＝[2/(2－1)]×2＝4米/秒 　由①式得 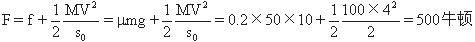　　　 　物块离开车板后作平抛运动，其水平速度v，设经历的时间为t₁，所经过的水平距离为s₁，则有 　　　　　　　　s₁=vt₁　　 　　　　　⑧ 　　　　　　　　h ＝(1/2)gt₁²　　　　　⑨　 　由⑨式得 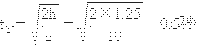　　　　　　 　　　　　　　　s₁=2×0.5=1米 　物块离开平板车后，若车的加速度为a则a＝F/M＝500/100＝5米/秒² 　车运动的距离 　　　 　于是 　　　　　　s=s₂-s₁=2.6-1=1.6米 　评分标准:全题8分 　正确求得物块开始离开车板时刻的物块速度v给1分，车的速度V给2分;求得作用于车的恒力F再给1分。 　正确求得物块离开车板后平板车的加速度给1分。 　正确分析物块离开车板后的运动，并求得有关结果，正确求出物块下落过程中车的运动距离s₂并由此求s的正确数值，共给3分。最后结果有错，不给这3分。 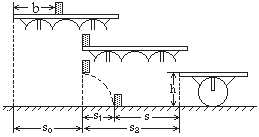　　　　　　　　 　解法二: 　设作用于平板车的水平恒力为F，物块与车板间的摩擦力为f，自车启动至物块离开车板经历的时间为t，在这过程中，车的加速度为a₁，物块的加速度为a₂。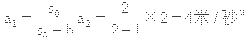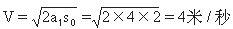则有 　　　　　　F-f=Ma₁　　　　　　① 　　　　　　　f=ma₂　 　　　　　② 　　　　　　　f=μmg　　 　　　　　③ 　以及 　　　　　　s₀＝(1/2)a₁t₁²　　　　④ 　　　　　　s₀－b＝(1/2)a₁t₁²　　　　⑤ 　由②、③两式得 　　　　　　a₂=μg=0.2×10=2米/秒² 　由④、⑤两式得 　　　 　由①、③两式得 　　　F=μmg+Ma₁=0.2×50×10+100×4=500牛顿 　物块开始离开车板时刻，物块和车的速度分别为v和V，则 　　　　 　　　　 　物块离车板后作平抛运动，其水平速度为v，所经历的时间为t₁，走过的水平距离为s₁，则有 　　　　　　s₁=vt₁　 　　　　　　⑥ 　　　　　　h＝(1/2)gt₁²　　　　　　⑦ 　解之得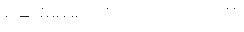： 　　　 　　　　　　s₁=vt₁=2×0.5=1米 　在这段时间内车的加速度 　　　　a＝F/M＝500/100＝5米/秒² 　车运动的距离 　　　 　　　　　s=s₂-s₁=2.6-1=1.6米 　评分标准:全题8分 　正确求得物块离开车板前，物块和车的加速度a₁、a₂，占2分，求得物块开始离开车板时刻的速度v和此时车的速度V占1分，求得作用于车的恒力F占1分。 　正确求得物块离开车板后，车的加速度a占1分。 　正确分析物块离开车板后物块的运动并求得有关结果，正确求得物块下落过程中车的运动距离，并由此求得s的正确结果，共占3分。最后结果错误，不给这3分。

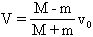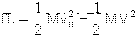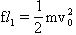1、解: 　　(1)A刚好没有滑离B板，表示当A滑到B板的最左端时，A、B具有相同的速度。设此速度为V， 　　A和B的初速度的大小为v₀，则由动量守恒可得: 　　　 Mv0－mv0＝(M+m)V 　　解得：　，　方向向右　　① 　　(2)A在B板的右端时初速度向左，而到达B板左端时的末速度向右，可见A在运动过程中必经历向左作减速运动直到速度为零，再向右作加速运动直到速度为V的两个阶段。设l₁为A开始运动到速度变为零过程中向左运动的路程， l₂为A从速度为零增加到速度为V的过程中向右运动的路程，L为A从开始运动到刚到达B的最左端的过程中B运动的路程，如图所示。设A与B之间的滑动摩擦力为f，则由功能关系可知: 　　对于B　　　　② 　　对于A　　　　　　③ 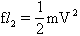　　　　　　　　　　④ 　　由几何关系L+(ι1－ ι2)＝ι　　　⑤ 　　由①、②、③、④、⑤式解得 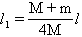　　　　　⑥ 　评分标准:本题8分 (1)2分。末速度的大小和方向各占1分。 (2)6分。其中关于B的运动关系式(例如②式)占1分；关于A的运动关系式(例如③、④两式)占3分，只要有错，就不给这3分；几何关系(例如⑤式)占1分；求出正确结果⑥，占1分。用其它方法求解，正确的，可参考上述评分标准进行评分。如考生若直接写出②、③、④、⑤的合并式

　　　　 则此式可给2分，再写出③式再给3分；最后结果正确再给1分。

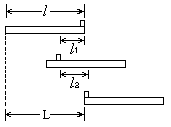
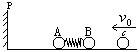
14、(2000年)(14分)在原子核物理中，研究核子与核关联的最有效途径是“双电荷交换反应”。这类反应的前半部分过程和下述力学模型类似。两个小球A和B用轻质弹簧相连，在光滑的水平直轨道上处于静止状态。在它们左边有一垂直于轨道的固定挡板P，右边有一小球C沿轨道以速度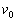射向B球，如图所示。C与B发生碰撞并立即结成一个整体D。在它们继续向左运动的过程中，当弹簧长度变到最短时，长度突然被锁定，不再改变。然后，A球与挡板P发生碰撞，碰后A、D都静止不动，A与P接触而不粘连。过一段时间，突然解除锁定(锁定及解除定均无机械能损失)。已知A、B、C三球的质量均为m。 (1)求弹簧长度刚被锁定后A球的速度。 (2)求在A球离开挡板P之后的运动过程中，弹簧的最大弹性势能。

答案：

13、(2000年)(12分)2000年1月26日我国发射了一颗同步卫星，其定点位置与东经98°的经线在同一平面内。若把甘肃省嘉峪关处的经度和纬度近似取为东经98°和北纬α=40°，已知地球半径R、地球自转周期T、地球表面重力加速度g(视为常量)和光速c。试求该同步卫星发出的微波信号传到嘉峪关处的接收站所需的时间(要求用题给的已知量的符号表示)

12、(99年)(12分)为了安全，在公路上行驶的汽车之间应保持必要的距离，已知某高速公路的最高限速为120 km/h假设前方车辆突然停止，后车司机从发现这一情况；经操纵刹车，到汽车开始减速所经历的时间(即反应时间)t＝0.50s，刹车时汽车受到阻力的大小f 为汽车重力的0.40倍该高速公路上汽车间的距离厅至少应为多少？取重力加速度g＝10m/s²

11、(99年)(12分)试在下述简化情况下由牛顿定律导出动量守恒定律的表达式：系统是两个质点，相互作用力是恒力，不受其他力，沿直线运动要求说明推导过程中每步的根据，以及式中各符号和最后结果中各项的意义。

10、(98年)(12分)一段凹槽A倒扣在水平长木板C上，槽内有一小物块B，它到槽两内侧的距离均为l/2，如图所示。木板位于光滑水平的桌面上，槽与木板间的摩擦不计，小物块与木板间的摩擦系数为μ。A、B、C三者质量相等，原来都静止。现使槽A以大小为v₀的初速向右运动，已知v₀<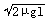 。当A和B发生碰撞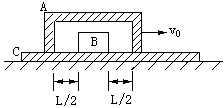时，两者速度互换。求： 　 (1)从A、B发生第一次碰撞到第二次碰撞的时间内，木板C运动的路程。 　 (2)在A、B刚要发生第四次碰撞时，A、B、C三者速度的大小。