第一节　 基础写作(共1小题，满分15分)

2010年， 第十六届亚运会将在广州举行。 广州亚组委正在为宣传册征集稿件。 请你根据以下信息，用英语写一篇介绍主办城市 --- 广州市的文章参与投稿。

　[写作内容]

参考词汇: 珠江三角洲 the Pearl River Delta　　 海上丝绸之路　 the Maritime Silk Road

　　　　　 始发港 a starting port　　

　[写作要求]只能用5个句子表达全部内容；

　[评分标准]句子结构准确，信息内容完整，篇章结构连贯。

第二节　 听取信息(共5小题；每小题1分，满分5分)

听下面一段独白，请根据题目要求，从所听到的内容中获取必要的信息，填入答题卡标号为16-20的空格中。听录音前，你将有10秒钟的阅题时间。录音读两遍，你将有80秒钟的作答时间。

Phillis　 Wheatley

第一节　 听力理解(5段共15小题；每小题2分，满分30分)

每段播放两遍。各段后有几个小题，各段播放前每小题有5秒钟的阅题时间。请根据各段播放内容及其相关小题，在5秒钟内从题中所给的A、B、C项中，选出最佳选项，并在答题卡上将该项涂黑。

听第一段对话材料，回答第1-3题。

1． What does the woman want David to do ?

A. Get the bottle on the top of the shelf.　　　　　　　　

B. Get the cover off the bottle.

C. Pick up some clothes.

2． Why was Alex out ?

A. He was out to work.

B. He wanted to buy an umbrella.

C. The woman asked him to fetch some clothes.

3． What happened to Alex?

A. He was caught in the rain.

B. He lost his umbrella.

C. He couldn't find his dry clothes,

听第二段材料，回答第4-6题。

4. Where does the conversation take place?

　 A. At the airport.　　　　　　 B. At home.　　　　　　 C. In a petrol station.

5. Why is the man not going to the airport at once?

　 A. He wants to stay at home for a while.

　 B. He wants to fill in the car with petrol first.

　 C. He thinks it's too early.

6. How are the two speakers going to the airport?

　 A. By bus.　　　　　　　　 B. By car.　　　　　　　 C. By taxi.

听第三段材料，回答第7-9题。

7. How does the woman want to go to Hawaii?

　 A. She insists on flying there.

　 B. She prefers to go there by ship.　　　

　 C. She prefers to go there by harbour crossing (海底隧道).　

8. What's the man's opinion?

　 A. Air transport is the safest.

　 B. Air transport is safe compared with road transport.

　 C. Air transport is safer than water transport.

9. What's the woman's opinion about her choice?

　 A. It's neither fast nor relaxing.

　 B. It's both fast and relaxing.

　 C. Though it's not fast, it's relaxing.　　

听第四段材料，回答第10-12题。

I0. Which of the following is true?

　 A. Newcastle is in the northeast of England.

　 B. Newcastle is a big city.

　 C. Newcastle has one of the biggest shopping centers in the world.

11. What's the main industry of Newcastle now?

　 A. Shipbuilding.　　　　 　　B. Coal-mining.　　 　　　　C. Chemical and soap industries.

12. Why does the speaker miss Newcastle so much ?

　 A. Because of the River Tyne.

　 B. Because of the friendly people and nice countryside,

　 C. Because he is a "Georgie".

听第五段材料，回答第13-15题。

13. When does the conversation take place?

　 A. On Monday.　　　　 　　　B. On Tuesday.　　 　　　　C. On Wednesday.

14. Which of the following is NOT true?

　 A. The man was a new patient to Dr Lee.

　 B. The man usually pick up his kids from school at about 4 o'clock.

　 C. The man was a driver.

15. What does the woman think of the man’s case ?

　 A. It doesn’t matter.　　 　　　B. It’s serious.　　　　 　　　C. It’s common.

例1．已知长方体的全面积为11,其12条棱的长度之和为24,则这个长方体的一条对角线长为(　　 ).

(A)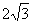　　　 (B)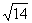　　 (C)5　　　 (D)6

分析及解：设长方体三条棱长分别为x,y,z,则依条件得：

　2(xy+yz+zx)=11,4(x+y+z)=24.而欲求的对角线长为,因此需将对称式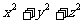写成基本对称式x+y+z及xy+yz+zx的组合形式,完成这种组合的常用手段是配方法.故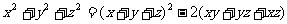=6²-11=25

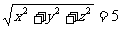∴　 ,应选C.

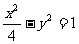例2．设F₁和F₂为双曲线的两个焦点,点P在双曲线上且满足∠F₁PF₂=90°,则ΔF₁PF₂的面积是(　　 ).　　　　　　　

(A)1　　　 (B)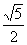　　 (C)2　　　 (D)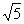_{[来源:Z|X|X|K]}

分析及解：欲求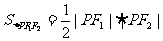　　　　 (1),而由已知能得到什么呢？

由∠F₁PF₂=90°,得　　　 (2),

又根据双曲线的定义得|PF₁|-|PF₂|=4　　　 (3),那么(2)、(3)两式与要求的三角形面积有何联系呢？我们发现将(3)式完全平方,即可找到三个式子之间的关系.即,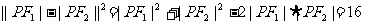

故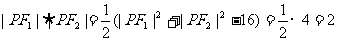

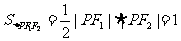∴　 ,∴　 选(A).

注：配方法实现了“平方和”与“和的平方”的相互转化.

例3．设双曲线的中心是坐标原点,准线平行于x轴,离心率为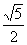,已知点P(0,5)到该双曲线上的点的最近距离是2,求双曲线方程.

分析及解：由题意可设双曲线方程为,∵,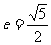∴a=2b,因此所求双曲线方程可写成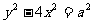：　 (1),故只需求出a可求解.

设双曲线上点Q的坐标为(x,y),则|PQ|=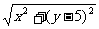　 (2),∵点Q(x,y)在双曲线上,∴(x,y)满足(1)式,代入(2)得|PQ|=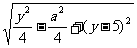　 (3),此时|PQ|²表示为变量y的二次函数,利用配方法求出其最小值即可求解.

由(3)式有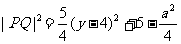(y≥a或y≤-a).

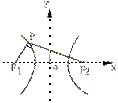
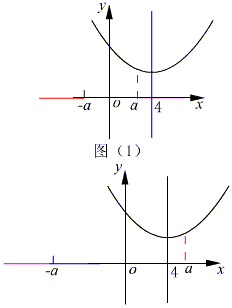二次曲线的对称轴为y=4,而函数的定义域y≥a或y≤-a,因此,需对a≤4与a>4分类讨论.

(1)当a≤4时,如图(1)可知函数在y=4处取得最小值,

∴令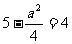,得a²=4

∴所求双曲线方程为.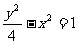

(2)当a>4时,如图(2)可知函数在y=a处取得最小值,

∴令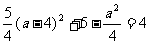,得a²=49,

∴所求双曲线方程为.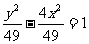

注：此题是利用待定系数法求解双曲线方程的,其中利用配方法求解二次函数的最值问题,由于二次函数的定义域与参数a有关,因此需对字母a的取值分类讨论,从而得到两个解,同学们在解答数习题时应学会综合运用数学思想方法解题.

例4．设f(x)是一次函数,且其在定义域内是增函数,又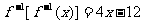,试求f(x)的表达式.

分析及解：因为此函数的模式已知,故此题需用待定系数法求出函数表达式.

设一次函数y=f(x)=ax+b　 (a>0),可知　 ,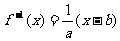

∴.

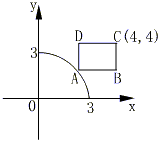比较系数可知：　 　_[来源:]

解此方程组,得　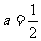 ,b=2,∴所求f(x)=.

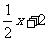例5．如图,已知在矩形ABCD中,C(4,4),点A在曲线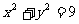(x>0,y>0)上移动,且AB,BC两边始终分别平行于x轴,y轴,求使矩形ABCD的面积为最小时点A的坐标.

分析及解：设A(x,y),如图所示,则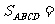(4-x)(4-y)　　　　　 (1)

此时S表示为变量x,y的函数,如何将S表示为一个变量x(或y)的函数呢？有的同学想到由已知得x²+y²=9,如何利用此条件？是从等式中解出x(或y),再代入(1)式,因为表达式有开方,显然此方法不好.

如果我们将(1)式继续变形,会得到S=16-4(x+y)+xy　 　　　　　　(2)

这时我们可联想到x²+y²与x+y、xy间的关系,即(x+y)²=9+2xy.

因此,只需设t=x+y,则xy=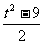,代入(2)式

得　　 S=16-4t+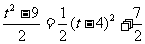(3)S表示为变量t的二次函数,

∵0<x<3,0<y<3,∴3<t<,∴当t=4时,S_ABCD的最小值为.

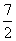此时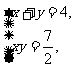

注：换元前后新旧变量的取值范围是不同的,这样才能防止出现不必要的错误.

例6．设方程x²+2kx+4=0的两实根为x₁,x₂,若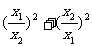≥3,求k的取值范围.

解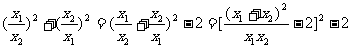：∵≥3,

以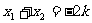,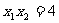代入整理得(k²-2)²≥5,又∵Δ=4k²-16≥0,

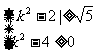∴解得k∈(-)∪[,+].

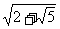例7．点P(x,y)在椭圆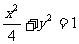上移动时,求函数u=x²+2xy+4y²+x+2y的最大值.

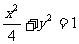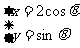解：∵点P(x,y)在椭圆上移动,　 ∴可设　　 于是

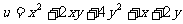
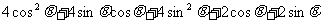　 　　　　=_{[来源:学#科#网]}

　　　　　 =

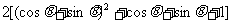
　　 令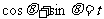, 　　∵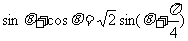,∴|t|≤.

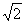　　 于是u=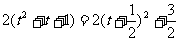,(|t|≤).

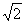　　 当t=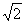,即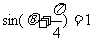时,u有最大值.

　　 ∴θ=2kπ+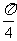(k∈Z)时,.

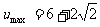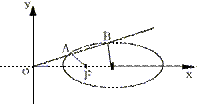例8．过坐标原点的直线l与椭圆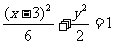相交于A,B两点,若以AB为直径的圆恰好通过椭圆的左焦点F,求直线l的倾斜角.

解：设A(x₁,y₁),B(x₂,y₂)

　　 直线l的方程为y=kx,将它代入椭圆方

程整理得 　(*)

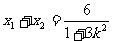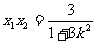由韦达定理,(1),(2)

　　 又F(1,0)且AF⊥BF,∴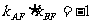,　　 即　 ,

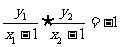　　 将,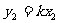代入上式整理得　 ,

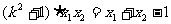　　 将(1)式,(2)式代入,解得　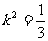 .　　 故直线l的倾斜角为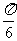或.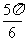

注：本题设交点坐标为参数,“设而不求”,以这些参数为桥梁建立斜率为k的方程求解.

例9．设集合A={}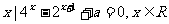

(1)若A中有且只有一个元素,求实数a的取值集合B；

(2)当a∈B时,不等式x²-5x-6<a(x-4)恒成立,求x的取值范围.

解：(1)令t=2^x,则t>0且方程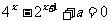化为t²-2t+a=0　 (*),A中有且只有一个元素等价于方程(*)有且只有一个正根,再令f(t)=t²-2t+a,

则Δ=0　 或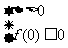即a=1或a≤0,从而B=(-,0]∪{1}.

(2)当a=1时,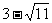<x<3+,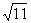

当a≤0,令g(a)=a(x-4)-(x²-5x-6),则当a≤0时不等式　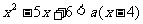 恒成立,

即当a≤0时,g(a)>0恒成立,故　 ≤4.

综上讨论,x的取值范围是(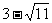,4).