
20.解:(I)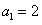 ,
,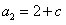 ,
,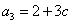 ,
,
因为 ,
, ,
,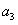 成等比数列,
成等比数列,
所以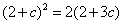 ,
--- 2分
,
--- 2分
解得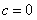 或
或 .
--- 4分
.
--- 4分
∵c≠0,∴ .
--- 5分
.
--- 5分
(2)当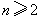 时,由于
时,由于
 ,
,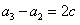 ,
,
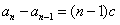 ,
,
所以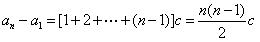 .
--- 8分
.
--- 8分
又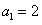 ,
, ,故
,故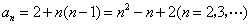 .
.
当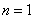 时,上式也成立,
时,上式也成立,
所以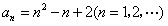 .
--- 10分
.
--- 10分
(3)令 --- 11分
--- 11分
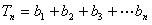
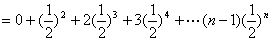 ……①
……①
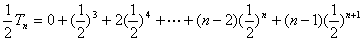 ……②
……②
①-②得: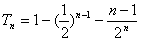 ---14分
---14分
19.解:(1)四棱锥P-ABCD的底面是边长为1的正方形,
侧棱PC⊥底面ABCD,且PC=2. ………………2分
设点C到平面PDB的距离为d,
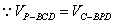 ,
, 

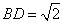 ,
, 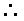
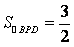 ,
, 

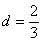 ---------------------------7分
---------------------------7分
(2)以点C为坐标原点,CD所在的直线为x轴建立空间直角坐标系如图示:
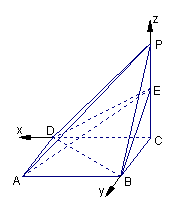 则
则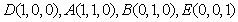 ,从而
,从而 ……………… 9分
……………… 9分
设平面ADE和平面ABE的法向量分别为

由法向量的性质可得: ,
,
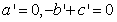
令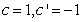 ,则
,则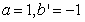 ,
,
∴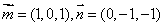 ………12分
………12分
设二面角D-AE-B的平面角为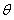 ,则
,则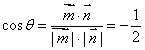
∴  ………………………………… 14分
………………………………… 14分
18.解: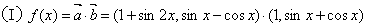
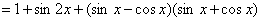 ………………………… 2分
………………………… 2分
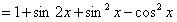
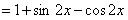 ……………………………………… 4分
……………………………………… 4分
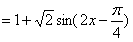 ……………………………………… 6分
……………………………………… 6分
∴当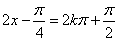 ,即
,即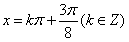 时,
时,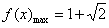 .……… 7分
.……… 7分
(Ⅱ)解 :由(Ⅰ)知, 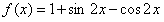
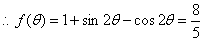 .
.
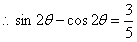 ,两边平方,得
,两边平方,得
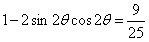 . …… 10分
. …… 10分
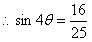 ……………………………… 12分
……………………………… 12分
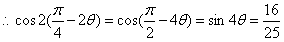 …………………………14分
…………………………14分
15.  16.
16. 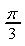 17.①④
17.①④ ②③ 或 ①③
②③ 或 ①③ ②④
②④
11. 12. -1 13.
15 14. 2
12. -1 13.
15 14. 2
22.已知 ,函数
,函数 .
.
(1)设曲线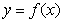 在点
在点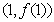 处的切线为
处的切线为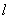 ,若
,若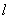 与圆
与圆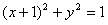 相切,
相切,
求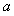 的值;
的值;
(2)求函数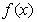 的单调区间; (3)求函数
的单调区间; (3)求函数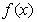 在[0,1]上的最小值。
在[0,1]上的最小值。
台州中学2009-2010学年第一学期期中答案
高三 数学(理)
21.已知椭圆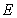 的中心在坐标原点,焦点在坐标轴上,且经过
的中心在坐标原点,焦点在坐标轴上,且经过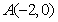 、
、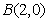 、
、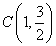 三点.
(1)求椭圆
三点.
(1)求椭圆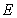 的方程:
的方程:
(2)若点D为椭圆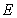 上不同于
上不同于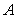 、
、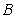 的任意一点,
的任意一点,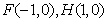 ,
,
当 内切圆的面积最大时。求内切圆圆心的坐标;
内切圆的面积最大时。求内切圆圆心的坐标;
(3)若直线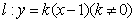 与椭圆
与椭圆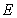 交于
交于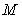 、
、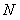 两点,
两点,
证明直线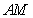 与直线
与直线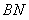 的交点在定直线上并求该直线的方程.
的交点在定直线上并求该直线的方程.
20.数列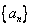 中,
中,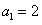 ,
,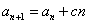 (
(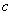 是不为零的常数,
是不为零的常数,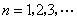 ),
),
且 成等比数列.
成等比数列.
(1)求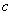 的值; (2)求
的值; (2)求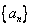 的通项公式;
的通项公式;
(3)求数列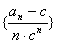 的前
的前 项之和
项之和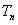 .
.
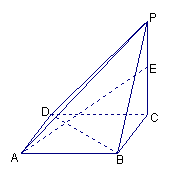
19.已知四棱锥P-ABCD,底面是边长为1的正方形,
侧棱PC长为2,且PC⊥底面ABCD,
E是侧棱PC上的动点。
(Ⅰ) 求点C到平面PDB的距离;
(Ⅱ) 若点E为PC的中点,
求平面ADE与平面ABE所成的锐二面角的大小.
18.已知向量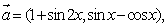
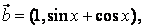 设函数
设函数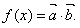
(Ⅰ)求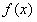 的最大值及相应的
的最大值及相应的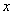 的值;
的值;
 (Ⅱ)若
(Ⅱ)若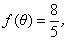 求
求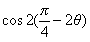 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com