
8.1944年,美国科学家艾弗里和他的同事,从S型活细菌中提取了DNA、蛋白质和多糖等物质,然后分别加入培养R型细菌的培养基中。结果发现只有加入DNA的培养基中,R型细菌转化成了S型细菌,而加入蛋白质和多糖的培养基中,R型细菌不能发生这种变化。这一现象说明了
①S型细菌的性状是由DNA决定的 ②在转化过程中,S型细菌的DNA可能进入到R型细菌细胞中
③DNA是遗传物质 ④S型细菌的DNA是遗传物质,R型细菌的DNA不是遗传物质
⑤蛋白质和多糖不是遗传物质 ⑥蛋白质和多糖在该转化实验中,起对照作用
A.①②③ B.①②③⑤ C.①②③⑤⑥ D.①②③④⑤⑥
7.1928年格里菲思做的肺炎双球菌转化实验,成功地表明了
A.DNA是遗传物质 B.DNA是主要的遗传物质
C.已经加热杀死的S型细菌中,含有能促成R型细菌发生转化的活性物质
D.已经加热杀死的S型细菌中,其中的DNA已失去活性而蛋白质仍具有活性
6. DNA分子在复制完成后,新合 成的那条子链的脱氧核苷酸的序列应与
成的那条子链的脱氧核苷酸的序列应与
A.模板母链相同 B.非模板母链相同
C.两条模板母链相同 D.两条模板母链都不相同
5.在下列四种化合物的化学组成中,与“A”所对应的名称相符合的是

A.①─腺嘌呤核糖核苷酸 B.②─腺苷
C.③─ 腺嘌呤脱氧核苷酸 D.④─腺嘌呤
腺嘌呤脱氧核苷酸 D.④─腺嘌呤
4.下图1是某生物的一个初级精母细胞,图2是该生物的五个精细胞。最可能来自同一个次级精母细胞的是
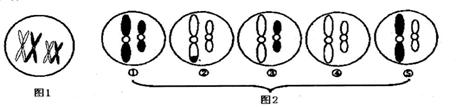
A.①和② B.②和④ C.③和⑤ D.①和④
3.把兔子血红蛋白的信使RNA加入至大肠杆菌的提取液中,结果能合成出兔子的血红蛋白,这说明
A.所有的生物共用一套遗传密码 B.兔血红蛋白的合成基因进入大肠杆菌
C.蛋白质的合成过程很简单 D.兔子的DNA可以指导大肠杆菌的蛋白质合成
1. 下面是科学家探索基因的历程,
①1866年孟德尔的豌豆杂交实验:提出遗传因子(基因)
②1903年萨顿研究蝗虫的精子和卵细胞形成过程,提出假说:基因在染色体上
③1910年摩尔根进行果蝇杂交实验:找到基因在染色体上的实验证据
他们在研究的过程所使用的科学研究方法依次为
A.①假说一演绎法 ②假说一演绎 ③类比推理
B.①假说一演绎法 ②类比推理 ③类比推理
C.①假说一演绎法
②类 比推理 ③假说一演绎法
比推理 ③假说一演绎法
D.①类比推理 ②假说一演绎法 ③类比推理
 2.对于下列式子,正确的说法有
2.对于下列式子,正确的说法有
①表示DNA复制过程; ②表示DNA转录过程; ③式中共有5种碱基;
④式中共有8种核苷酸 ⑤式中共5种核苷酸 ⑥式中的A均代表同一种核苷酸
A.①②③ B.②⑤⑥ C.②③④ D.①③⑤
19、(本小题13分)已知 , 其中向量
, 其中向量 ,点
,点 在
在 的图像上, 且点
的图像上, 且点 为
为 的图像与
的图像与 轴的交点.若数列
轴的交点.若数列 为等差数列, 且公差为1,
为等差数列, 且公差为1,  .
.
(1) 求数列 ,
,  的通项公式;
的通项公式;
(2) 求 的最小值;
的最小值;
(3) 记 , 且
, 且
 ,问是否存在
,问是否存在 ,使得
,使得 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
解: (1) 由 ,
,  , 得:
, 得:
 …………………… (1)
…………………… (1)
即

 为与
为与 轴的交点,
轴的交点,
 则
则 
 20、(本小题14分)已知函数
20、(本小题14分)已知函数 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)数列 满足:
满足: ,且
,且 ,记数列
,记数列 的前n项和为
的前n项和为 ,且
,且 ;试求:
;试求:
①求数列 的通项公式;并判断
的通项公式;并判断 是否仍为数列
是否仍为数列 中的项?若是,请证明;否则,说
中的项?若是,请证明;否则,说
明理由.
 ②记
②记 ,求数列
,求数列 的前
的前 项和
项和 .
.
当 时,
时, ,
,
当 时,
时, ,
,
所以 .
……………………………(8分)
.
……………………………(8分)
又因为 ,
,
所以令 ,则
,则
得到 与
与 矛盾,所以
矛盾,所以 不在数列
不在数列 中. ………(10分)
中. ………(10分)


 的逆矩阵.
的逆矩阵.
解: ,即
,即 ,
,
所以 得
得 ……………………(4分)
……………………(4分)
即M=
 ,由
,由 得
得
 .
.
或
 =1
=1 ,
, 
 . ……………………(7分)
. ……………………(7分)
(2)(选修4-4:极坐标及参数方程)
已知曲线C的极坐标方程是 ,设直线l的参数方程是
,设直线l的参数方程是 (t为
(t为
参数).判断直线l和曲线C的位置关系.

16、(本小题13分)已知函数 的图象在点B(1,
的图象在点B(1, )处的切线的斜率为-3.
)处的切线的斜率为-3.
(1)求 、
、 的值;
的值;
(2)若不等式 对于
对于 恒成立,求
恒成立,求 的取值范围.
的取值范围.

 图像与函数
图像与函数 相邻两交点间的距离为
相邻两交点间的距离为
 即
即 …………5分
…………5分
 …………7分
…………7分
(2)由平移公式得
 得平移后的解析式为
得平移后的解析式为 …………9分
…………9分
 平移后的图像关于原点对称
平移后的图像关于原点对称  …………11分
…………11分
 时,
时, 的最小值为
的最小值为 …………13分。
…………13分。

∴ ⊥
⊥ ,而EF
,而EF 平面ACD1,
平面ACD1,
∴EF∥平面ACD1……………………………………………………(6分)
(2) ∵ =(0,2,0),cos<
=(0,2,0),cos< ,
, >=
>=
∴异面直线EF与AB所成角的余弦值为 ……………………(9分).
……………………(9分).
(3)设点P(2,2,t)(0<t≤2),平面ACP的一个法向量为 =(x,y,z),
=(x,y,z),
 解法二:(1)同解法一知
解法二:(1)同解法一知 =
= (-1,2,-1) ,
(-1,2,-1) , =(-2,0,2),
=(-2,0,2),
 = (-2,2,0),∴
= (-2,2,0),∴ -
-
 =
= ,
,
∴ 、
、 、
、 共面.
共面.
又∵EF 平面ACD1,∴EF∥平面ACD1. ……………………………(6分)
平面ACD1,∴EF∥平面ACD1. ……………………………(6分)
(2)、(3)同解法一.
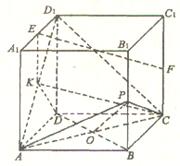 解法三:(1)取AD1的中点K,连结EK、KC,在△AA1D1
解法三:(1)取AD1的中点K,连结EK、KC,在△AA1D1
中,EK∥AA1,且EK= AA1,
AA1,
 ∵FC=
∵FC= CC1,CC1∥AA1,∴FC EK,
CC1,CC1∥AA1,∴FC EK,
∴四边形EKCF为平行四边形,
∴EF∥CK.又∵CK 平面ACD1,
平面ACD1,
EF 平面ACD1,∴EF∥平面ACD1. (4分)
平面ACD1,∴EF∥平面ACD1. (4分)
 二面角P-AC-B的大小为30°. ……………………………………(13分)
二面角P-AC-B的大小为30°. ……………………………………(13分)
 解法四:(1)取D1C1的中点H,连结EH,FH,A1C1,
解法四:(1)取D1C1的中点H,连结EH,FH,A1C1,
∵E为A1D1的中点,∴EH∥AlCl,
而A1C1∥AC,∴EH∥AC,
又∵F为CC1的中点,∴HF∥D1C.
∵EH与HF相交,D1C与AC相交,
∴平面EHF∥平面ACD1,EF 平面EHF,
平面EHF,
∴E F∥平面ACD1. ………………(4分)
F∥平面ACD1. ………………(4分)
(2)、(3)同解法三.
 成立,则实数t的取值范围是
成立,则实数t的取值范围是  .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com