
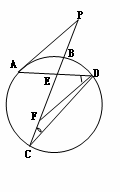
22.(选修4-1:几何证明选讲)
如图所示,已知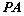 与⊙
与⊙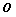 相切,
相切,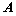 为切点,
为切点,
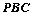 为割线,弦
为割线,弦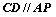 ,
,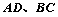 相交于
相交于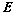 点,
点,
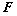 为
为 上一点,且
上一点,且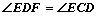 .
.
(1)求证: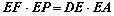 ;
;
(2)若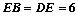 ,
, ,求
,求 的长.
的长.
21.(本小题满分12分)
设点 为曲线
为曲线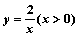 上任一点,以点
上任一点,以点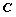 为圆心的圆与
为圆心的圆与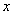 轴交于点
轴交于点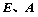 ,与
,与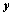 轴交于点
轴交于点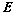 、
、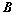 .
.
(1)证明:多边形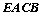 的面积是定值,并求这个定值;
的面积是定值,并求这个定值;
(2)设直线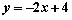 与圆
与圆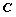 交于点
交于点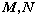 ,若
,若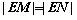 ,求圆
,求圆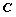 的方程.
的方程.
20. (本小题满分12分)
数列{an}是首项为23,公差为整数的等差数列,且第六项为正,第七项为负。
⑴求数列的公差;
⑵求前n项和Sn的最大值;
⑶当Sn>0时,求n的最大值。
19.(本小题满分12分)
已知a为实数,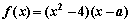 。
。
⑴求导数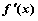 ;
;
⑵若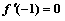 ,求
,求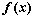 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
18.(本小题满分12分)
已知过点A(0,1)的直线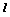 ,斜率为k,与圆C:(x-2)2+(y-3)2=1相交于M、N两个不同点
,斜率为k,与圆C:(x-2)2+(y-3)2=1相交于M、N两个不同点
(1)求实数k取值范围;
(2)若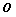 为坐标原点,且
为坐标原点,且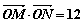 ,求k的值。
,求k的值。
17.(本小题满分12分)
已知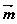 =(cos
=(cos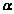 ,sin
,sin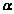 ),
),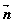 =(cos
=(cos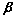 ,sin
,sin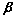 ),0<
),0<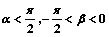 ,|
,|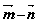 |=
|=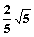 ,
,
求sin(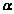 -
-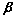 ).
).
16.定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和。
已知数列{an}是等和数列,且a1=2,公和为5,那么a18的值为______________,这个数列的前n项和Sn的计算公式为________________
15.若过点(m,2)总可以作两条直线和圆(x+1)2 +(y-2)2=4相切,则实数m的取值范围是_________。
14. 向量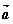 =(-2,3),
=(-2,3),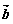 =(1,m),若
=(1,m),若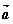 、
、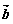 夹角为钝角,则实数m的范围是_________
夹角为钝角,则实数m的范围是_________
13.将直线y=-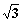 x+2
x+2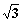 绕点A(2,0)按顺时针方向旋转30°所得到的直线方程是_________
绕点A(2,0)按顺时针方向旋转30°所得到的直线方程是_________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com