
(1)建议教学用实例来讲述1弧度的含义,这样便于学生概念的理解;
(2)建议在教学时,通过弧度制与角度制对比来分析、说明应用弧度制的度量比应用角度制的度量方法是否具有优越性;
(3)关于弧度与角度二者的换算,教学时应抓住:
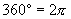 弧度
弧度 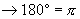 弧度
弧度
这个关键,来引导学生;
(4)教学应注意强调在同一式中,所采用的单位必须一致;
(5)通过例3的教学,应让学生知道,无论是利用角度制还是弧度制,都能在已知弧长和半径的情况下推出扇形面积公式,但利用弧度制来推导要简单中些.
教学设计示例(一)
弧度制
教学目标:
1.明确引入弧度制的必要性,理解新单位制意义.
重点是理解弧度的意义,能正确地进行角度制与弧度制的换算;难点是弧度制的概念与角度的关系。
(1)要弄清1弧度的意义。弧度制与角度制一样,只是度量角的一种方法,但由于学生有先入为主的想法,所以学起来有一定的困难,首先必须清楚1弧度的概念,它与所在圆的半径大小无关。其次弧度制与角度制相比有一定的优点,一是在进位上角度制在度、分、秒上是60进制,而弧度制却是十进制,其二在弧长和扇形的面积的表示上弧度制也比角度制简单: 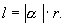
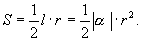
(2)两种制度的转换。利用它们的意义在弧度制下圆周角为 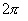 rad,而角度制下圆周角为
rad,而角度制下圆周角为 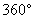 ,所以
,所以
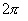 rad=
rad= 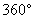 ,进而得到
,进而得到
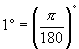 rad
rad 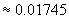 rad.
rad.
1rad 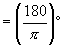
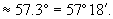
1.使学生理解弧度的意义,能正确地进行弧度与角度的换算,熟记特殊角的弧度数; 2.了解角的集合与实数集R之间可以建立起一一对应的关系; 3.掌握弧度制下的弧长公式,会利用弧度解决某些简单的实际问题; 4.在理解弧度制定义的基础上,领会弧度制定义的合理性; 5.通过学习,理解并认识角度制与弧度制都是对角度量的方法,二者是辩证统一的.
教学建议
4.2 弧度制
教学目标
16. 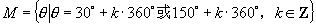 ,
,
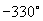 ,
,
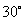 ,
,
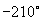 ,
,
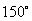 .
.
提示:先由 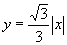 可知所求角在
可知所求角在
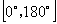 的值为
的值为
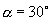 或
或
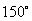 ,由此即可写出集合
,由此即可写出集合
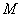 .
.
15.所求集合为 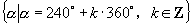 ,集合中绝对值最小的角为
,集合中绝对值最小的角为
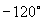 .
.
14. 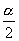 在第二、四象限;
在第二、四象限;
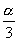 在第一、三、四象限.
在第一、三、四象限.
13.阴影部分角的集合为 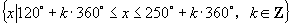 ,
,
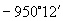 是该集合中的角.因为
是该集合中的角.因为
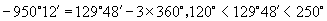 .
.
12.由 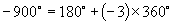 ,知符合条件的角为
,知符合条件的角为
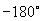 ,
,
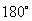 ,
,
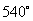 ,
,
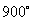 ,
,
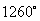 .
.
11.(1) 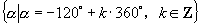 ,其中
,其中
 的最小正角为
的最小正角为
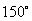 ,最大负角为
,最大负角为
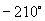 ;
;
(2) 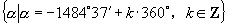 ,其中
,其中
 的最小正角为
的最小正角为
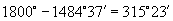 ,最大负角为
,最大负角为
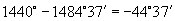 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com