
3.练习反馈
(1) 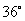 =___________弧度;
=___________弧度; 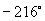 =____________弧度;-10弧度_________度
=____________弧度;-10弧度_________度
(2)与 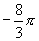 终边相同的角是__________,它们是第__________象限角,其中最小正角为__________,最大负角为___________.
终边相同的角是__________,它们是第__________象限角,其中最小正角为__________,最大负角为___________.
参考答案:
(1) 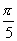 ;
;
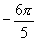 ;
;
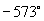
(2) 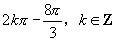 ;它们是第三象限角;最小正角为
;它们是第三象限角;最小正角为
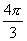 ,最大负角为
,最大负角为
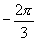 .
.
2.探索研究
(1)正、负角的弧度定义.
 正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,角
正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,角  的弧度数的绝对值
的弧度数的绝对值
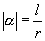 ,
,
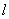 为以角
为以角
 作为圆心角的所对的弧的长,
作为圆心角的所对的弧的长,
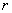 是圆的半径,这种以弧度作为单位来度量角的单位制,叫做弧度制.
是圆的半径,这种以弧度作为单位来度量角的单位制,叫做弧度制.
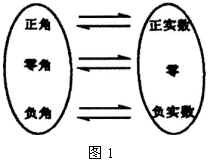
(2)角集合与实数集 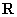 之间的一一对应
之间的一一对应
用弧度制来度量角,实际上是在角的集合与实数集
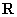 之间建立这样的一一对应关系(如图1所示).
之间建立这样的一一对应关系(如图1所示).
每一个角都有惟一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有惟一的一个角(角的弧度数等于这个实数)与它对应.
于是,就可以把三角函数看成是以实数为自变量的函数,它的自变量的意义可以有多种解释,从而使三角函数的应用更加广泛,在数学与科学研究中所以普遍采用弧度制,这是原因之一.
(3)有关公式
①弧长 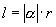
② 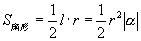
(4)例题分析
[例1]下列站个角中哪几个是第二象限角?
(1) 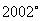 (2)
(2) 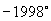 (3)
(3) 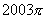
(4)9 (5)-4 (6) 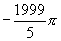
解:(1) 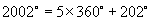
(2) 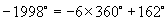
(3) 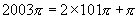
(4) 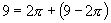
(5) 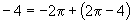
(6)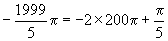
从而可知(2)(4)(5)所给的角在Ⅱ象限.
点评:①用弧度制表示终边相同的角的方法
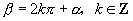
②把一角化为 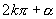 形式,其中
形式,其中
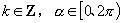 从而可判断角所在象限.
从而可判断角所在象限.
③在同一问题求解过程中,两种单位不能混用,如
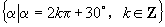 写法不妥.
写法不妥.
[例2](1)把 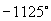 化为
化为
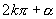 ,
,
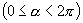 ,
,
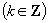 的形式是( )
的形式是( )
A. 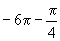 B.
B. 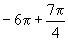 C.
C. 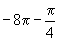 D.
D. 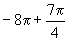
(2)在半径不等的两个圆内,1弧度的圆心角( )
A.所对弧长相等 B.所对的弦长相等
C.所对弧长等于各自半径 D.所对的弧长为 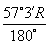
解:∵ 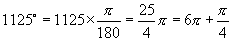
∴ 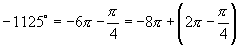
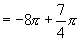
∴选D.
(2)由弧度制定义,知半径为 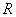 的圆上,1弧度的弧长应等于半径
的圆上,1弧度的弧长应等于半径 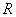 ,故选
,故选
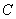 .
.
[例3]填空
(1)在 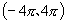 内找出与
内找出与
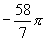 终边相同的角______________.
终边相同的角______________.
(2)圆的弧长等于该圆内接正三角形的边长,则该弧所对的圆心角的弧度数是________________.
(3)在扇形 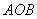 中,
中,
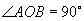 ,弧长为1,则此扇形内切圆的面积____________.
,弧长为1,则此扇形内切圆的面积____________.
解:(1)与 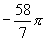 终边相同角,设为
终边相同角,设为
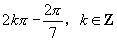 .令
.令
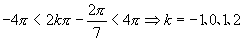
∴所求角为: 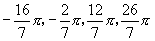 .
.
 (2)设圆半径为
(2)设圆半径为 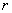 ,则内接正三角形边长为
,则内接正三角形边长为
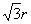 ,当弧长
,当弧长
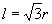 时,其所对圆心角
时,其所对圆心角
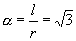 .
.
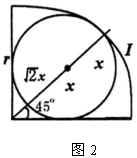
(3)如图2,设扇形半径为 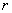 ,内切圆半径为
,内切圆半径为
 ,则由
,则由
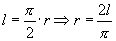
∵ 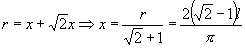
∴ 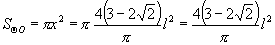
1.设置情境.
像角的概念推广一样,我们已经把
 -
-
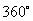 中角,利用“乘以
中角,利用“乘以
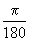 ”这一法则映射到实数集
”这一法则映射到实数集
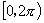 上,那么,
上,那么,
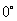 -
-
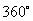 以外的角能否化为弧度制?如果能,如何转化呢?乘数因子是否仍为“
以外的角能否化为弧度制?如果能,如何转化呢?乘数因子是否仍为“
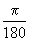 ”,本节课就来讨论这个问题.
”,本节课就来讨论这个问题.
2.能灵活应用弧长公式、扇形面积公式解决问题.
教学重点:能熟练地进行角度制与弧度制的互化.
教学难点:能灵活应用弧长公式、扇形面积公式解决问题.
教学用具:投影仪
教学过程:
1.理解角集与实数集 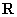 的一一对应,熟练掌握角度制与弧度制间的互相转化.
的一一对应,熟练掌握角度制与弧度制间的互相转化.
6.已知一个扇形周长为 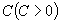 ,当扇形的中心角为多大时,它有最大面积
,当扇形的中心角为多大时,它有最大面积
参考答案:1.C 2.D
3.6; 4. 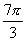 或
或
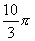 ; 5.
; 5.  ; 6.中心角
; 6.中心角  时,
时,
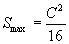 .
.
教学设计示例(二)
弧度制
教学目标
5.已知直径为 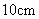 的滑轮上有一条长为
的滑轮上有一条长为
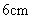 的弦,
的弦,
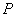 是此弦的中点,若滑轮以每秒5弧度的角速度旋转,则经过5秒钟后点
是此弦的中点,若滑轮以每秒5弧度的角速度旋转,则经过5秒钟后点 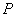 转过的弧长等于多少?
转过的弧长等于多少?
4.若 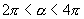 ,且
,且
 与
与
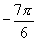 的角的终边垂直,则
的角的终边垂直,则
 .
.
3.中心角为 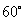 的扇形,它的弧长为
的扇形,它的弧长为
 ,则该扇形所在圆的半径为______________.
,则该扇形所在圆的半径为______________.
2.若角  和
和
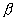 的终边互为反向延长线,则有( )
的终边互为反向延长线,则有( )
A.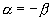 B.
B. 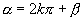
C. 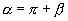 D.
D. 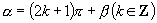
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com