
1.(1) 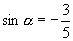 ,
,
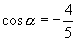 ,
,
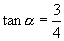 ,
,
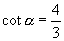 ,
,
 ,
,

(2)  ,
,
 ,
,
 ,
,  ,
,
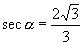 ,
, 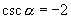
3.化简
(1)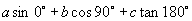
(2)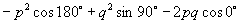
(3)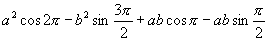
(4)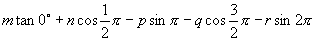
参考答案:
2.计算
(1)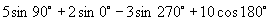
(2)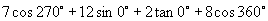
(3)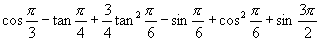
(4)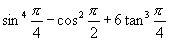
1.已知角  的终边经过下列各点,求角
的终边经过下列各点,求角
 的六个三角函数值.
的六个三角函数值.
(1) 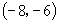 (2)
(2) 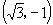
4.本课小结
利用定义求三角函数值,首先要建立直角坐标系,角顶点和始边要按既定的位置设置.角
 的三角函数定义式,其实是比例的化身,它的背后是相似形在支称着,不过这个定义具有一般性,如轴上角的三角函数,如果没有定义作为论据,欲求其函数性就不是很容易.
的三角函数定义式,其实是比例的化身,它的背后是相似形在支称着,不过这个定义具有一般性,如轴上角的三角函数,如果没有定义作为论据,欲求其函数性就不是很容易.
分类讨论(角位置)是三角函数求值过程中,使用频率非常高的一个数学思想,而分类标准往往是四个象限及四个坐标半轴.
课时作业:
3.反馈训练
(1)若角  终边上有一点
终边上有一点
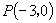 ,则下列函数值不存在的是( ).
,则下列函数值不存在的是( ).
A. 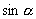 B.
B. 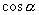 C.
C.  D.
D. 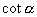
(2)函数 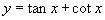 的定义域是( ).
的定义域是( ).
A.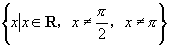 B.
B. 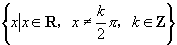
C. 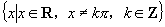 D.
D. 
(3)若 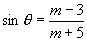 ,
,
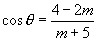 都有意义,则
都有意义,则
 .
.
(4)若角 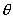 的终边过点
的终边过点
 ,且
,且
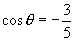 ,则
,则
 .
.
参考答案:(1)D;(2)B;(3) 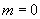 或8,说明点
或8,说明点 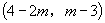 在半径为
在半径为
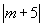 的圆上;(4)-6.
的圆上;(4)-6.
2.探索研究
(1)复习回忆锐角三角函数
我们已经学习过锐角三角函数,知道它们都是以锐角
 为自变量,以比值为函数值,定义了角
为自变量,以比值为函数值,定义了角
 的正弦、余弦、正切、余切的三角函数,本节课我们研究当角
的正弦、余弦、正切、余切的三角函数,本节课我们研究当角
 是一个任意角时,其三角函数的定义及其几何表示.
是一个任意角时,其三角函数的定义及其几何表示.
(2)任意角的三角函数定义
如图1,设  是任意角,
是任意角,
 的终边上任意一点
的终边上任意一点
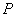 的坐标是
的坐标是
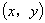 ,当角
,当角
 在第一、二、三、四象限时的情形,它与原点的距离为
在第一、二、三、四象限时的情形,它与原点的距离为
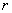 ,则
,则
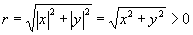 .
.
定义:①比值 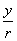 叫做
叫做
 的正弦,记作
的正弦,记作
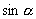 ,即
,即
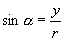 .
.
②比值  叫做
叫做
 的余弦,记作
的余弦,记作
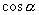 ,即
,即
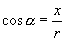 .
.
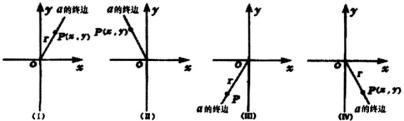
图1
③比值 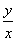 叫做
叫做
 的正切,记作
的正切,记作
 ,即
,即
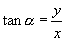 .
.
同时提供显示任意角的三角函数所在象限的课件
提问:对于确定的角  ,这三个比值的大小和
,这三个比值的大小和
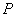 点在角
点在角
 的终边上的位置是否有关呢?
的终边上的位置是否有关呢?
利用三角形相似的知识,可以得出对于角
 ,这三个比值的大小与
,这三个比值的大小与
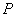 点在角
点在角
 的终边上的位置无关,只与角
的终边上的位置无关,只与角
 的大小有关.
的大小有关.
请同学们观察当 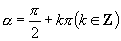 时,
时,
 的终边在
的终边在
 轴上,此时终边上任一点
轴上,此时终边上任一点
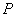 的横坐标
的横坐标
 都等于0,所以
都等于0,所以 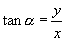 无意义,除此之外,对于确定的角
无意义,除此之外,对于确定的角
 ,上面三个比值都是惟一确定的.把上面定义中三个比的前项、后项交换,那么得到另外三个定义.
,上面三个比值都是惟一确定的.把上面定义中三个比的前项、后项交换,那么得到另外三个定义.
④比值  叫做
叫做
 的余切,记作
的余切,记作
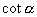 ,则
,则
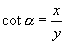 .
.
⑤比值 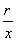 叫做
叫做
 的正割,记作
的正割,记作
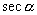 ,则
,则
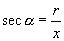 .
.
⑥比值 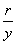 叫做
叫做
 的余割,记作
的余割,记作
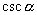 ,则
,则
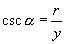 .
.
可以看出:当 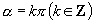 时,
时,
 的终边在
的终边在
 轴上,这时
轴上,这时
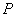 的纵坐标
的纵坐标
 都等于0,所以
都等于0,所以 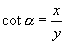 与
与
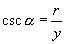 的值不存在,当
的值不存在,当
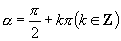 时,
时,
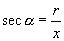 的值不存在,除此之外,对于确定的角
的值不存在,除此之外,对于确定的角
 ,比值
,比值
 ,
,
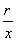 ,
,
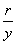 分别是一个确定的实数,所以我们把正弦、余弦,正切、余切,正割及余割都看成是以角为自变量,以比值为函数值的函数,以上六种函数统称三角函数.
分别是一个确定的实数,所以我们把正弦、余弦,正切、余切,正割及余割都看成是以角为自变量,以比值为函数值的函数,以上六种函数统称三角函数.
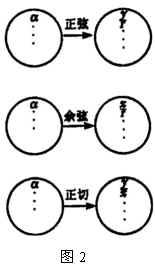 (3)三角函数是以实数为自变量的函数
(3)三角函数是以实数为自变量的函数
对于确定的角  ,如图2所示,
,如图2所示, 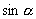 ,
,
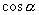 ,
,
 分别对应的比值各是一个确定的实数,因此,正弦,余弦,正切分别可看成从一个角的集合到一个比值的集合的映射,它们都是以角为自变量,以比值为函数值的函数,当采用弧度制来度量角时,每一个确定的角有惟一确定的弧度数,这是一个实数,所以这几种三角函数也都可以看成是以实数为自变量,以比值为函数值的函数.
分别对应的比值各是一个确定的实数,因此,正弦,余弦,正切分别可看成从一个角的集合到一个比值的集合的映射,它们都是以角为自变量,以比值为函数值的函数,当采用弧度制来度量角时,每一个确定的角有惟一确定的弧度数,这是一个实数,所以这几种三角函数也都可以看成是以实数为自变量,以比值为函数值的函数.
即:实数→角(其弧度数等于这个实数)→三角函数值(实数)
(4)三角函数的一种几何表示
利用单位圆有关的有向线段,作出正弦线,余弦线,正切线,如下图3.
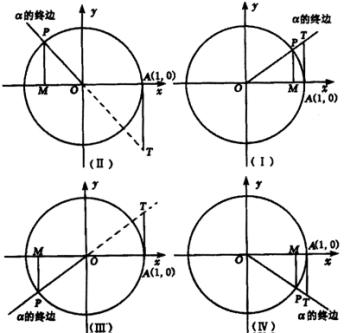
图3
设任意角  的顶点在原点
的顶点在原点
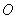 ,始边与
,始边与
 轴的非负半轴重合,终边与单位圆相交于点
轴的非负半轴重合,终边与单位圆相交于点
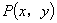 ,过
,过
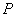 作
作
 轴的垂线,垂足为
轴的垂线,垂足为
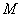 ;过点
;过点
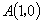 作单位圆的切线,这条切线必然平行于轴,设它与角
作单位圆的切线,这条切线必然平行于轴,设它与角
 的终边(当
的终边(当
 为第一、四象限时)或其反向延长线(当
为第一、四象限时)或其反向延长线(当
 为第二、三象限时)相交于
为第二、三象限时)相交于
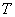 ,当角
,当角
 的终边不在坐标轴上时,我们把
的终边不在坐标轴上时,我们把
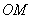 ,
,
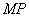 都看成带有方向的线段,这种带方向的线段叫有向线段.由正弦、余弦、正切函数的定义有:
都看成带有方向的线段,这种带方向的线段叫有向线段.由正弦、余弦、正切函数的定义有:
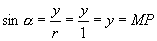
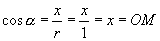
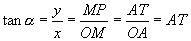
这几条与单位圆有关的有向线段
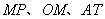 叫做角
叫做角
 的正弦线、余弦线、正切线.当角
的正弦线、余弦线、正切线.当角
 的终边在
的终边在
 轴上时,正弦线、正切线分别变成一个点;当角
轴上时,正弦线、正切线分别变成一个点;当角
 的终边在
的终边在
 轴上时,余弦线变成一个点,正切线不存在.
轴上时,余弦线变成一个点,正切线不存在.
(5)例题讲评
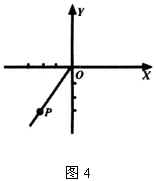 [例1]已知角
[例1]已知角  的终边经过
的终边经过
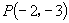 ,求
,求
 的六个三角函数值(如图4).
的六个三角函数值(如图4).
解:∵ 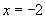
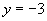
∴ 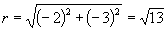
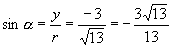
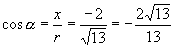
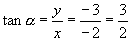
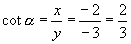
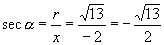
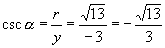
提问:若将 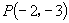 改为
改为

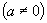 ,如何求
,如何求
 的六个三角函数值呢?(分
的六个三角函数值呢?(分
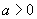 ,
,
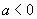 两种情形讨论)
两种情形讨论)
[例2]求下列各角的六个三角函数值
(1) 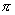 ;(2)
;(2) 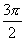 ;(3)
;(3)  .
.
解:(1)∵当 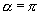 时,
时,
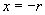 ,
,
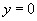
∴  ,
,
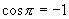 ,
,

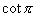 不存在,
不存在, 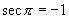 ,
,
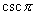 不存在
不存在
(2)∵当 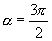 时,
时,
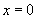 ,
,
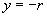
∴ 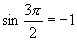 ,
,
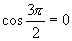
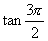 不存在
不存在 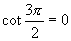
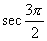 不存在
不存在 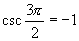
(3)当 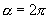 时,
时,
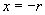 ,
,
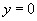
∴ 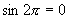
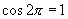
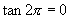
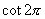 不存在
不存在
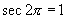
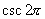 不存在
不存在
[例3]作出下列各角的正弦线,余弦线,正切线.(1) 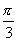 ;(2)
;(2) 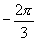 .
.
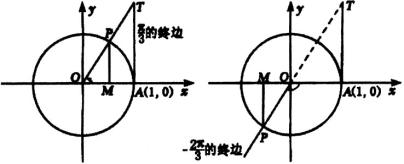
解: 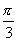 ,
,
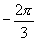 的正弦线,余弦线,正切线分别为
的正弦线,余弦线,正切线分别为
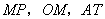 .
.
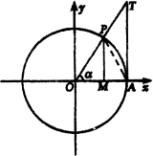 [例4]求证:当
[例4]求证:当  为锐角时,
为锐角时,
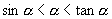 .
.
证明:如右图,作单位圆,当
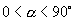 时作出正弦线
时作出正弦线
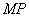 和正切线
和正切线
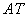 ,连
,连
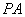
∵ 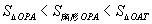
∴ 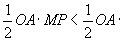
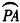
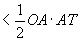
∴ 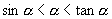
利用三角函数线还可以得出如下结论
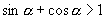 的充要条件是
的充要条件是  为第一象限角.
为第一象限角.
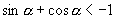 的充要条件是
的充要条件是  为第三象限角.
为第三象限角.
练习(学生板演,利用投影仪)
(1)角  的终边在直线
的终边在直线
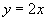 上,求
上,求
 的六个三角函数值.
的六个三角函数值.
(2)角  的终边经过点
的终边经过点
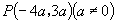 ,求
,求
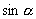 ,
,
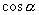 ,
,
 ,
,
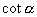 的值.
的值.
(3)说明 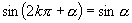 的理由.
的理由.
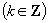 .
.
解答:
(1)先确定终边位置
①如  在第一象限,在其上任取一点
在第一象限,在其上任取一点
 ,
,
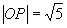 ,则
,则
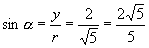 ,
, 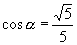
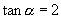
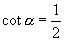
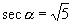
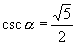
②如  在第三象限,在终边上任取一点
在第三象限,在终边上任取一点
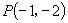
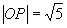 ,则
,则
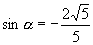 ,
, 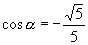
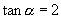
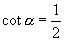

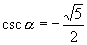
(2)若 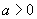 ,不妨令
,不妨令
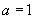 ,则
,则
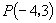 在第二角限
在第二角限
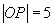
∴ 
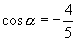
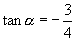
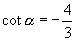
(3)在  终边上任取一点
终边上任取一点
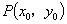 ,因为
,因为
 与
与
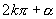 终边相同,故
终边相同,故
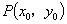 也为角
也为角
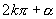 终边上一点,所以
终边上一点,所以
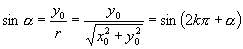 成立.
成立.
说明:以后会知道,求三角函数值的方法有多种途径.用定义求角
 的三角函数值,是基本方法之一.当角终边不确定时,要首先确定终边位置,然后再在终边上取一个点来计算函数值.
的三角函数值,是基本方法之一.当角终边不确定时,要首先确定终边位置,然后再在终边上取一个点来计算函数值.
1.设置情境
角的范围已经推广,那么对任一角
 是否也能像锐角一样定义其四种三角函数呢?本节课就来讨论这一问题.
是否也能像锐角一样定义其四种三角函数呢?本节课就来讨论这一问题.
2.掌握已知角  终边上一点坐标,求四个三角函数值.(即给角求值问题)
终边上一点坐标,求四个三角函数值.(即给角求值问题)
教学重点:
任意角的三角函数的定义.
教学难点:
任意角的三角函数的定义,正弦、余弦、正切这三种三角函数的几何表示.
教学用具:
直尺、圆规、投影仪.
教学步骤:
(1)由三角函数的定义可知,若已知角 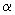 终边上一点,便可求出其各三角函数值,或通过三角函数定义,可知其二求其一.
终边上一点,便可求出其各三角函数值,或通过三角函数定义,可知其二求其一.

三角函数的符号与角所在象限有关,采用上图来记忆.
(2)必须讲清并强调 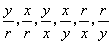 这六个比值的大小都与点
这六个比值的大小都与点
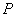 在角的终边上的位置无关,只与角的大小有关,即它们都是以角为自变量,以比值为函数值的函数.
在角的终边上的位置无关,只与角的大小有关,即它们都是以角为自变量,以比值为函数值的函数.
(3)教学中应注意,语言要准确严密.首先“六种函数统称为三角函数”这句话,说明不是这六种函数的函数,都不能说是三角函数.
(4)教学中,应当引导学生深刻认识三角函数符号的含义.如, 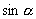 这个符号,它表示
这个符号,它表示
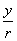 ,即角
,即角
 的正弦,不能把
的正弦,不能把
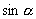 看成
看成
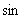 与
与
 的乘积,犹如
的乘积,犹如
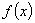 不能看成
不能看成
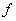 与
与
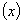 的乘积一样,离开了自变量
的乘积一样,离开了自变量
 ,符号
,符号
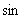 就没有意义了.同时也应注意,每个函数记号的第一个字母“
就没有意义了.同时也应注意,每个函数记号的第一个字母“
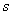 ”或“
”或“
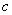 ”或“
”或“
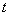 ”都不能大写,不能让学生养成写“
”都不能大写,不能让学生养成写“
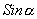 ”、“
”、“
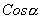 ”等习惯.
”等习惯.
教学设计示例(一)
任意角的三角函数
教学目标:
1.通过对初中锐角三角函数定义的回忆,掌握任意角三角函数的定义法,并掌握用单位圆中的有向线段表示三角函数值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com