
2.求值
(1) 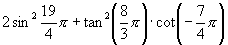
(2) 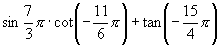
参考答案:
1.确定下列三角函数值的符号
(1) 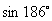 (2)
(2) 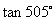 (3)
(3)
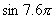
(4)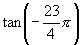 (5)
(5) 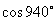 (6)
(6)
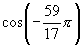
4.本课小结
(1)确定三角函数定义域时,主要应抓住三角函数定义中,比值的分母不得为零这一制约条件,当终边落在坐标轴上时,终边上任一点
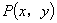 的坐标中,必有一分量为0,故相应有一比值无意义.
的坐标中,必有一分量为0,故相应有一比值无意义.
(2) 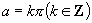 时,
时,
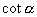 ,
,
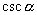 无意义,这两个函数定义域为
无意义,这两个函数定义域为
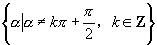
课时作业:
3.反馈练习
(1)已知  是第三象限角且
是第三象限角且
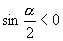 ,则( )
,则( )
A.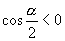 B.
B. 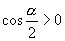 C.
C. 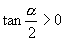 D.
D. 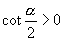
(2)下列各式为正号的是( )
A. 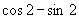 B.
B. 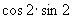
C. 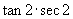 D.
D. 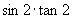
(3)若 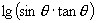 有意义,则
有意义,则
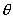 是( )
是( )
A.第一象限角 B.第四象限角
C.第一或第四象限角 D.第一或第四或  轴正半轴
轴正半轴
(4)已知  的终边过点
的终边过点
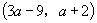 ,且
,且
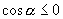 ,
,
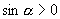 ,则
,则
 的取值范围是_____.
的取值范围是_____.
(5)函数 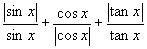 的值域是_____________.
的值域是_____________.
参考答案:(1)B;(2)C;(3)C;(4)  ;(5)
;(5) 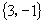
2.探索研究
(1)三角函数值的符号
今后我们还要经常用到三角函数在各个象限的符号,由于从原点到角的终边上任意一点的距离
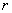 总是正值,根据三角函数定义可知,三角函数值符号取决于各象限内的坐标符号,请同学们分象限思考四个象限中三角函数值的符号.
总是正值,根据三角函数定义可知,三角函数值符号取决于各象限内的坐标符号,请同学们分象限思考四个象限中三角函数值的符号.
观察六个三角函数,可发现
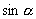 与
与
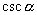 ,
,
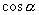 与
与
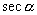 ,
,
 与
与
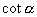 互为倒数,因此它们的符号规律相同.
互为倒数,因此它们的符号规律相同.
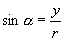 当
当  在第一、二象限时,
在第一、二象限时,
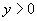 ,
,
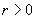 ,所以
,所以
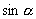 为正,而当
为正,而当
 在第三、四象限时,
在第三、四象限时,
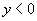 ,
,
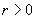 ,
,
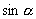 为负的.
为负的.
同理 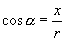 对于第一、四象限角是正的,而对于第二、三象限的角是负的.
对于第一、四象限角是正的,而对于第二、三象限的角是负的.
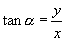 与
与 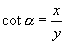 ,当
,当
 在第一、三象限时,
在第一、三象限时,
 与
与
 同号,所以
同号,所以
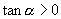 ,
,
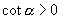 ,而当
,而当
 在第二、四象限时,
在第二、四象限时,
 与
与
 异号,
异号,
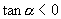 ,
,
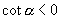 .
.
现在我们将以上讨论结果整理成图1.
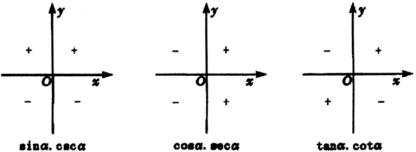
图1
可以表达为正弦和余割上正下负,余弦与正割左负右正,正切与余切一、三象限为正,二、四象限为负.同学们还可以自己用口诀“全正,
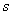 正,
正,
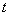 正,
正,
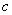 正”来记忆.
正”来记忆.
(2)诱导公式一
上节课我们已学过同终边的角,例如
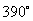 和
和
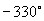 都与
都与
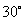 终边位置相同.
终边位置相同.
∵ 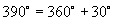
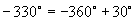
∴由三角函数定义可知它们的三角函数值相同,即
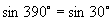
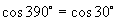
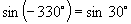
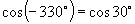
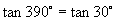
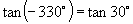
推广到一般情形,我们可得到诱导公式一:终边相同的角的同一三角函数值相等,即
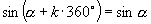
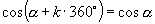

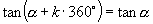
这组公式的作用是可把任意角的三角函数值问题转化为0-360°角的三角函数值问题.
(3)例题分析
[例1]确定下列三角函数值符号:
(1) 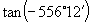 ;(2)
;(2) 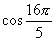 ;(3)
;(3) 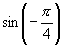
解:(1) 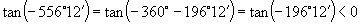
(2) 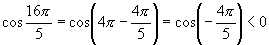
(3)∵ 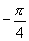 是第四象限角,∴
是第四象限角,∴
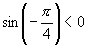
[例2]求证角 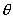 为第三象限角的充分必要条件是
为第三象限角的充分必要条件是
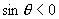 ,
,
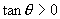 .
.
证明:
必要性:当 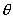 为第三象限角时,
为第三象限角时,
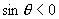 ,
,
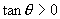 ;
;
充分性:∵ 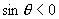 成立,∴
成立,∴
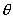 角的终边可能位于第三或第四象限,也可以位于
角的终边可能位于第三或第四象限,也可以位于
 轴的非正半轴上;又∵
轴的非正半轴上;又∵
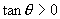 成立,∴
成立,∴
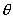 角的终边可能位于第一或第三象限,因为要同时成立,所以
角的终边可能位于第一或第三象限,因为要同时成立,所以
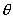 角的终边只可能位于第三象限,于是角
角的终边只可能位于第三象限,于是角
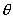 为第三象限角.
为第三象限角.
[例3]求下列三角函数值:
(1) 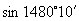 ;(2)
;(2) 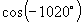 ;(3)
;(3) 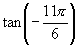 .
.
解:(1)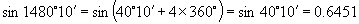
(2)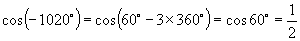
(3)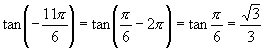
[例4]如果 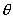 在第二象限,则
在第二象限,则
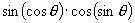 的值是什么符号?
的值是什么符号?
解:∵ 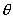 在第二象限,∴
在第二象限,∴
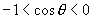
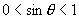
∴ 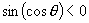 ,
,
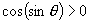 ∴
∴ 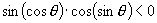
[例5]若  是第二象限的角,且
是第二象限的角,且
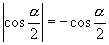 ,问
,问
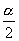 是第几象限角?
是第几象限角?
解:∵  是第二角限的角,
是第二角限的角,
∴ 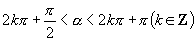
∴ 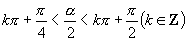
∴ 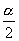 终边在第一或第三象限角,
终边在第一或第三象限角,
又∵ 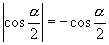 ∴
∴ 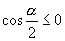
故 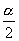 是第三象限的角.
是第三象限的角.
[例6]求值: 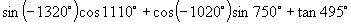
解:原式
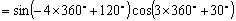
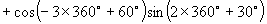
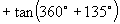
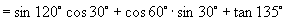
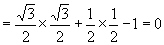
1.设置情境
设角 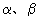 均是第二象限角,依三角函数定义,为了求
均是第二象限角,依三角函数定义,为了求
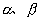 的四个三角函数值,只要分别在
的四个三角函数值,只要分别在
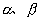 终边上取点
终边上取点
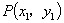 、
、
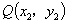 ,由比值
,由比值
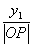 ,
,
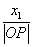 ,
,
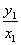 ,
,
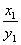 ,及
,及
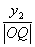 ,
,
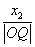 ,
,
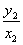 ,
,
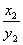 可知,这两组比值虽然不一定相等,但由于
可知,这两组比值虽然不一定相等,但由于
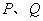 均在第二象限,故
均在第二象限,故
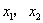 同号,
同号,
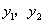 同号,因而可见,
同号,因而可见,
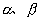 的正弦、余弦、正切、余切值,符号是对应相同时。那么,当
的正弦、余弦、正切、余切值,符号是对应相同时。那么,当
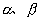 分别为一、三、四象限时,上述性质是否仍然成立呢?下面就可讨论这一问题.
分别为一、三、四象限时,上述性质是否仍然成立呢?下面就可讨论这一问题.
2.掌握诱导公式一,并能运用诱导公式把角  的三角函数值转化为
的三角函数值转化为
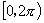 中角的三角函数值.
中角的三角函数值.
教学重点:
终边相同的角的同一三角函数值相等.
教学难点:
运用诱导公式把角
 的三角函数值转化为
的三角函数值转化为
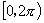 中角的三角函数值.
中角的三角函数值.
教学用具:
直尺、圆规、投影仪.
教学过程
1.根据任意角三角函数定义,归纳出三角函数在各象限的符号,并能根据角  的某种函数值符号,反馈出
的某种函数值符号,反馈出
 可能存在的象限.
可能存在的象限.
3.(1)0;(2) 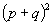 ;(3)
;(3) 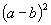 ;(4)
;(4) 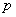
教学设计示例(二)
任意角的三角函数 第二课时
教学目标:
2.(1)-2;(2)8;(3)-1;(4) 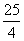
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com