
4.当 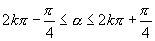 ,(
,(
 )时,化简
)时,化简
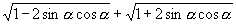 的结果是( )
的结果是( )
A. 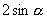 B.
B. 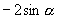 C.
C. 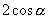 D.
D. 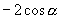
3.设 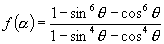 ,求
,求
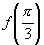 .
.
2.化简 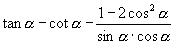
1.求证:
(1) 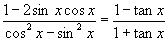
(2) 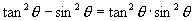
(3) 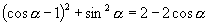
(4) 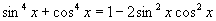
4.本课小结
(1)证明同角三角函数恒等式一般有“由繁到简”“中间会师”“变更论证”等方法,具体要求要由等式两端的特征(结构、名称)来选择最佳方法.
(2)整体代换、方程思想亦有常用之时.
(3)1的代换,往往会给化简、变换化来奇效,有“柳暗花明”之好处.
课时作业:
2.解:∵ 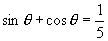 ①
① 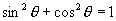
①两边平方: 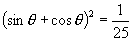
即 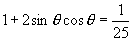 ∴
∴
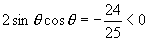
∵ 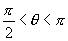 ∴
∴ 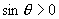
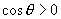
∴ 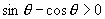
由 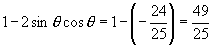
即 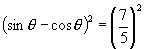
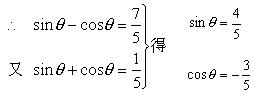
∴ 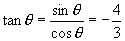
2.已知: 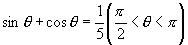 求
求
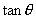 .
.
解:1.(1) 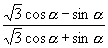

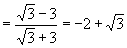
(2) 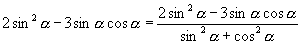
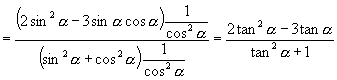
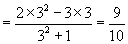
1.已知: 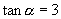 ,求(1)
,求(1) 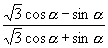 .
.
(2) 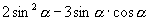 的值.
的值.
3.演练反馈(投影)
2.探索研究
(1)复习同角三角函数关系式
上一节课我们已经学习了同角三角函数关系式,请一位同学叙述出同角三角函数的三个关系式.
同角三角数关系式有
(1)平方关系: 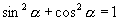
(2)商数关系: 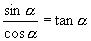
(3)倒数关系: 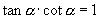
下面这组等式也是常用公式,请同学利用定义验证一下.
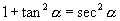 ,
, 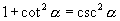 ,
,
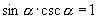 ,
, 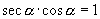 ,
,
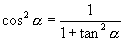 ,
,

化简三角式的基本思路:切、割化弦,和、差化积,“1”去代换等等.证明三角恒等式常用方法:单向证明,双向起动,证等价式等等.
代数公式,如  ,
,
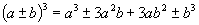 ,等也会常用.
,等也会常用.
(2)例题分析
①利用同角三角函数关系式求证三角恒等式及应用
[例1]求证 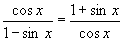
证法1:由 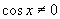 知
知
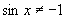 所以
所以

于是 左边 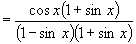

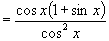
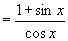 =右边
=右边
∴原式成立
证法2:∵ 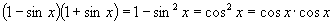
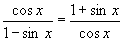
证法3:∵ 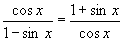
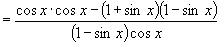
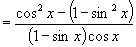
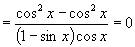
∴ 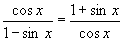
证法4:设角  终边上任一点
终边上任一点
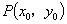 ,
,
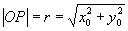 ,由定义,
,由定义,
左 
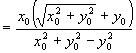
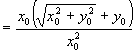
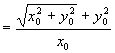
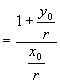
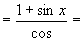 右
右
∴ 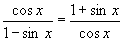
从上例可看出,证明一个等式,可以从它的任何一边开始,证得它等于另一边;还可以先证得另一个等式成立,从而推出需要证明的等式成立.
[例2]求证三角恒等式
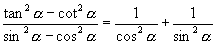
证明:左边 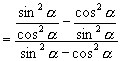
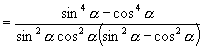
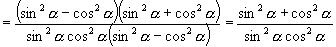
 右边
右边
∴等式得证
总结,当一个函数式中含有弦、切两类以上的函数,常将“切”函数化为“弦”函数,称为化弦法.
[例3]已知 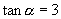 ,求:(1)
,求:(1) 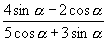 ;(2)
;(2) 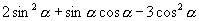 的值.
的值.
解:(1)分析1:为了直接利用 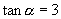 ,注意所求值式的分子、分母均为一项齐式(
,注意所求值式的分子、分母均为一项齐式(
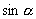 、
、
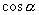 的次数相同),把分子、分母同除以
的次数相同),把分子、分母同除以
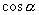 (
(
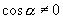 ),将分子、分母转化为
),将分子、分母转化为
 为元的代数式.
为元的代数式.
原式 

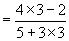
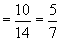
(2)∵ 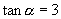
∴ 
∴原式 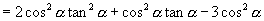
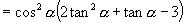
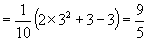
分析2:可利用平方关系 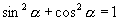 将分子、分母都变为二次齐次式,再利用商数关系式归为关于
将分子、分母都变为二次齐次式,再利用商数关系式归为关于
 的分式求值.
的分式求值.
解:原式 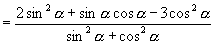
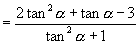
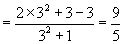
[例4]化简下列各式:
(1) 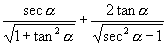 (
(
 为第三象限角);
为第三象限角);
(2) 
解:(1)∵  为第三象限角
为第三象限角
∴原式 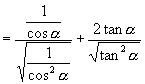
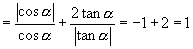
注:在运用同角三角函数关系式解题时要特别注意弄清楚角所在象限及其对应的三角函数的符号.

[例5]当 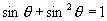 ,求
,求
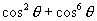 的值.
的值.
分析:本题关键是灵活地多次运用条件等式
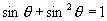 从而结合同角三角函数关系式达到降次求解的目标.
从而结合同角三角函数关系式达到降次求解的目标.
解:∵ 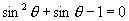 ∴
∴ 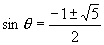
又∵ 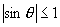 ∴
∴ 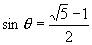
∵ 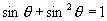 ∴
∴ 
∴ 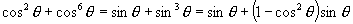
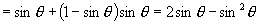
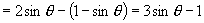
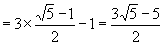
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com