
7. 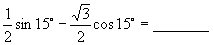 .
.
6.化简 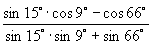 的结果是( )
的结果是( )
A. 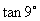 B.
B.  C.
C.  D.
D. 
5.若 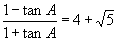 ,则
,则
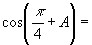 ( )
( )
A. 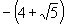 B.
B. 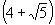 C.
C. 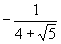 D.
D. 
4.已知  ,
,
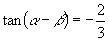 ,则
,则
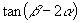 的值是( )
的值是( )
A. 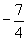 B.
B.  C.
C. 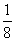 D.
D. 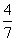
3.下列命题中是假命题的是( )
A.对任意的  和
和
 角,有
角,有
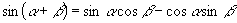 成立
成立
B.存在无穷多个  和
和
 角,使得
角,使得
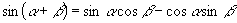 成立
成立
C.对任意的  和
和
 角,有
角,有
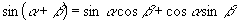 成立
成立
D.存在无穷多个  和
和
 角,使得
角,使得
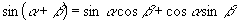 成立
成立
2.  等于( )
等于( )
A. 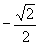 B.
B. 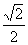 C.
C. 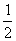 D.
D. 
1.  的值是( )
的值是( )
A. 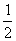 B.
B. 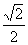 C.
C. 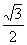 D.
D. 
(四)板书设计
|
课题:两角和与差的正弦 1.公式推导 ① 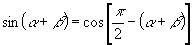  =……  得到公式……… 得到公式………
 把公式中  换成 换成
 得公式……… 得公式………
 2.公式的结构特点 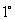 用单角函数表示复角函数
用单角函数表示复角函数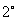 右边中两个积的函数名称不同
右边中两个积的函数名称不同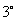 ……运算符号同左边括号 ……运算符号同左边括号中的运算符号一致(区别于  、 、
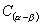 ) )3.折、凑角技巧 |
例1 例2 例3 |
例4 例5 演练反馈 总结提炼 |
典型例题
[典例剖析]
例1 化简与求值.
(1) 
(2) 
分析:可先用诱导公式将三角式中的角度转化,然后再用两角和与差的三角公式化简与求值.
解:(1)原式 
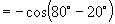
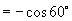
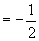
(2)原式 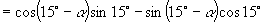

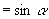
说明:本例第(1)题中四个角不相同,初看起来不能利用公式,但是当我们利用诱导公式将角度化为小于 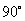 的正角后,就会发现其内在关系,而对于第(2)题中的
的正角后,就会发现其内在关系,而对于第(2)题中的 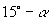 与
与
 ,由于它们互为补角,故也可用诱导公式化为相同的角.
,由于它们互为补角,故也可用诱导公式化为相同的角.
例2 求 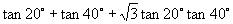 的值.
的值.
分析:发现此式与 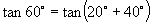 用和角正切公式展开后之间的内在联系,即可求得所求的值.
用和角正切公式展开后之间的内在联系,即可求得所求的值.
解:∵ 
去分母整理,得

说明:灵活运用公式体现在变形应用公式,如本例,和差角正切公式是分式形式,根据需要可化为整式.
3
已知  ,
,
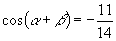 ,
,
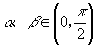 ,求
,求
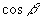 的值.
的值.
分析:由  的范围及
的范围及
 的值,利用同角三角函数关系式可求
的值,利用同角三角函数关系式可求
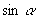 和
和
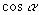 的值,同理可求得
的值,同理可求得
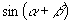 的值,再用已知角
的值,再用已知角
 及
及
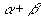 来表示未知角
来表示未知角
 ,即
,即
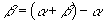 ,然后利用两角差的余弦公式求得.
,然后利用两角差的余弦公式求得.
解:∵  ,
,
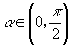
∴  .
.
∴ 
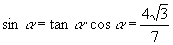
又∵ 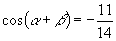 ,
,
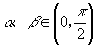
∴ 
于是 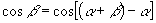

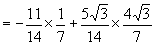
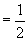
说明:本题获解的关键是将  表示成:
表示成:
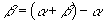 .由于可以求
.由于可以求
 与
与
 相应三角函数值,所以利用两角差的余弦公式可顺利求得
相应三角函数值,所以利用两角差的余弦公式可顺利求得
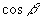 的值.
的值.
例4 已知: 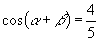 ,
,
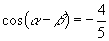 ,
,
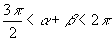 ,
,
 ,求
,求
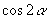 与
与
 .
.
分析:研究角与角的关系,发现
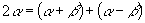 ,
, ,再求余弦值.
,再求余弦值.
解:∵ 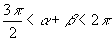 ,
,
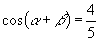 ,
,
∴ 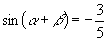
∵  ,
,
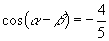 ,
,
∴ 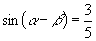
∴ 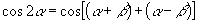


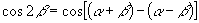


例5 已知: 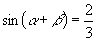 ,
,
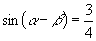 ,求
,求
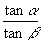 的值.
的值.
分析:欲求值,需化弦,得  ,可再求
,可再求
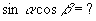 ,
,
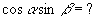
解:∵ 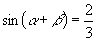 ,∴
,∴ 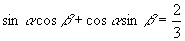 ①
①
∵ 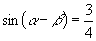 ,∴
,∴  ②
②
(①+②)÷(①-②)
得 
说明:当题中异角、异名时,常需化角化名,有时将单角转化为复角(和或差),本题是利用展开,将复角化成单角,正(余)切和正(余)弦常常互化.
例6 已知:  是△
是△
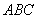 的三个内角,且
的三个内角,且
 .试判断此三角形的形状特征.
.试判断此三角形的形状特征.
分析:(1)化去对数符号,对数式转化为有理式,(2)考察  的关系及大小,据此判明形状特征.
的关系及大小,据此判明形状特征.
解:从  可得
可得
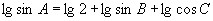 ,
,
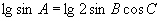 ,
,
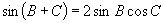
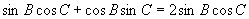 .
.
移项化为 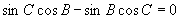
即  ∴
∴
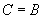
∴ △ 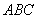 为等腰三角形.
为等腰三角形.
说明:(1)从角与角的关系探究三角函数间的关系;反之,利用三角函数间的关系去判断角的大小及关系,这是常用的基本方法.
(2)若此题用下面的方法继续探究下去,你认为怎样?为什么?
由于  ∴
∴ 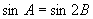 故
故 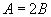 .
.
∵ 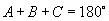 ∴
∴ 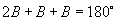 ,
,
得 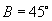 ,
,
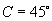 ,
,
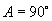 ,
,
∴ 此三角形是等腰直角三角形.
例7 在△ 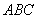 中,求证
中,求证
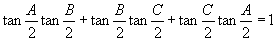 .
.
分析: 注意到 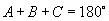 ,∴
,∴
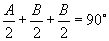 ,
,
移项得 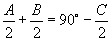 ,取正切,用诱导公式和
,取正切,用诱导公式和
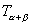 整理即是.另外,
整理即是.另外,
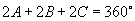 ,
,
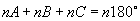
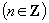 .都可得出相类拟的等式.
.都可得出相类拟的等式.
证明: ∵ 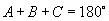 ∴
∴ 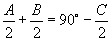
故 
即 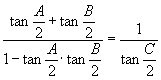
去分母得
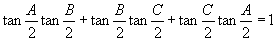
例8 已知: 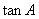 与
与
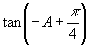 是
是
 的解,若
的解,若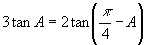 ,求
,求
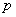 与
与
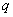 的值.
的值.
分析:∵ 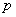 与
与
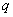 是二个未知数,∴列出二个方程便可解得.
是二个未知数,∴列出二个方程便可解得.
解:设  ,则
,则
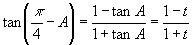 ,
,
∵ 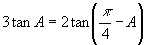 ,∴
,∴  ,
,
解得 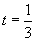 或
或
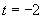 .
.
(Ⅰ)当 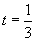 时,有
时,有
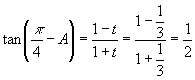 ,
,
∴ 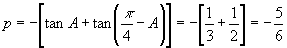 ,
,
 .
.
(Ⅱ)当 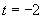 时,有
时,有
 .
.
∴ 
 .
.
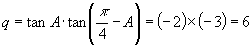
说明:“列方程求未知数”这是数学的常用方法,要熟悉方程的思想方法并会灵活运用,如果
 ,
,
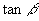 是某二次方程的二根,则韦达定理与公式
是某二次方程的二根,则韦达定理与公式
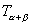 有着必然的联系;若
有着必然的联系;若
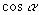 ,
,
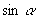 是某二次方程的二根,则韦达定理与
是某二次方程的二根,则韦达定理与
 有着必然联系,要充分利用这些联系解题.
有着必然联系,要充分利用这些联系解题.
扩展资料
月球有多远?多大?
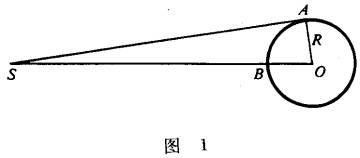
如图1,如果从地球上A点看,月球S刚好在地平线上(即AS和地球半径OA垂直),而同时从地球上B点看,S刚好在天顶处(即S在地球半径OB的延长线上),那么∠S就叫做月球S的地平视差。根据一个天体的地平视差,可以算出这个天体的距离。 ∠S可以从∠AOB算出,而∠AOB可以从地球上A、B两点的经纬度算出。 月球S的地平视差(∠S),就是从月球S看来,垂直于视线(SA)的地球半径(OA)所对的角。
已知地球半径R=6370千米,月球的地平视差是57ˊ,我们就可以计算月球离我们的距离。
在Rt△OAS中,

即月球离地球的距离是三十八万四千公里。
一般地,已知地球半径R,又已知一个天体的地平视差a,那么这个天体离地球的距离D可以从下式算出:
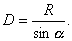
但是用这个方法测定天体的距离,只适用于较近的天体,例如太阳系的天体,如太阳、行星和地球的卫星等,对于更远的天体,如其他恒星,则因地平视差非常小,几乎等于零,这个方法就不适用,而要用其他的方法来测定它们的距离。由于需要的知识比较复杂,在此不加介绍。
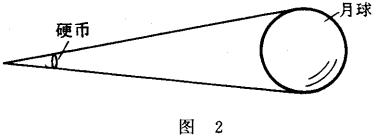
当我们已知月球离我们的距离时,就可以测定月球直径的大小。 如图2,把一个五分的硬币(直径2.4厘米),放在离眼睛2.6米的地方,大致能够把整个月面遮住。(试一试!)

如图3,由△OAB-△OCD,可得:
 (相似三角形对应高的比等于相似比)。
(相似三角形对应高的比等于相似比)。
把AB=0.024米,OF=384000000米,OE=2.6米代入,得
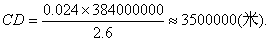
就是说,月球的直径约是3500公里。
另一种测定月球直径大小的方法,需要观测月球对地球上一点所张的视角θ(如图4)。
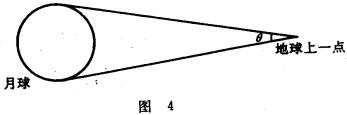
假如观测到月球对地球上一点所张的视角是32'。那么怎样计算出月球的大小呢? 如图5,设r是月球的半径,d是月球离地球的距离,θ是月球对地球上一点所张的视角。 利用直角三角形解法,


其中d=384000000米,
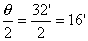 ,所以
,所以
r=384000000×sin16'
=384000000×0.00465
≈1790000(米)。
就是说,月球半径约是1790公里,即月球直径约是3580公里。
上面两种方法测得的月球的直径不一样,是因为测量难免有误差,不同的测量方法精确程度也不同,所测得的结果都是月球离地球距离的近似值的缘故。
现在如果告诉你太阳的地平视差是
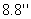 ,太阳对地球一点所张的视角恰好也是32',你应该会计算太阳与地球的距离及太阳直径的近似值了吧!不过在计算中需知的sin
,太阳对地球一点所张的视角恰好也是32',你应该会计算太阳与地球的距离及太阳直径的近似值了吧!不过在计算中需知的sin 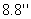 的值从我们常用的三角函数表中查不到,因此,还要告诉你sin
的值从我们常用的三角函数表中查不到,因此,还要告诉你sin 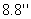 =0.0000427。至于怎么求出这个三角函数值,到了高中就能明白。太阳离地球的距离是一亿五千万公里,它的直径约是一百四十万公里。计算的结果是不是这样?
=0.0000427。至于怎么求出这个三角函数值,到了高中就能明白。太阳离地球的距离是一亿五千万公里,它的直径约是一百四十万公里。计算的结果是不是这样?
扩展资料
三角学的出现与第一张弦表的问世
在古代,三角学只是几何学中研究“三角形之量度”的那部分.使三角学从几何学中分离出来,成为一门独立学科的标志是第一张弦表的问世.
公元前二世纪中叶,古希腊的天文学家希巴诸斯,为了天文观察工作的需要,进行了造表的工作.他在一个固定的圆内,计算给定度数的圆弧
 所对应的弦
所对应的弦
 的长度.但是,希巴诸斯得到的一系列弦值,不是现代三角学理论中的正弦值,而是所谓的“全弦值”.
的长度.但是,希巴诸斯得到的一系列弦值,不是现代三角学理论中的正弦值,而是所谓的“全弦值”.
由于希巴诸斯的原著早已失传,所以关于他在三角学上的成就,人们是从托勒密的著作中得知的,因此有人就干脆把第一张弦表不叫做“希巴诸斯弦表”,而叫做“托勒密弦表”.
托勒密也是一位天文学家,他在公元二世纪中叶所著的“算学总览”一书中,给出了从  到
到
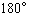 ,每隔半度的弦表.
,每隔半度的弦表.
在公元五世纪左右,印度数学家阿耶波多在造表工作中,不再研究对应于中心角
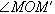 的全弦
的全弦
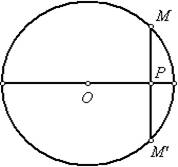
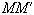 (如图),而是研究它的一半
(如图),而是研究它的一半
 ,这就是现代三角学中所称的角
,这就是现代三角学中所称的角
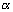 的正弦线,它把三角学的研究又推进了一步.
的正弦线,它把三角学的研究又推进了一步.
在公元九世纪左右,阿拉伯数学家阿尔·巴坦尼在吸收了托勒密全弦表和阿耶波多正弦表的优点的基础上,还造出了一张包含从  到
到
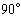 ,每隔
,每隔
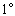 的余切表.半个多世纪后,阿布尔·威发又造出了间隔仅为
的余切表.半个多世纪后,阿布尔·威发又造出了间隔仅为  的正弦表和正切表,并首次引入正割和余割这两个概念,使六个三角函数概念全部出现了.
的正弦表和正切表,并首次引入正割和余割这两个概念,使六个三角函数概念全部出现了.
公元十二世纪,阿拉伯天文学家纳速拉丁总结了前期数学家在三角学上的成就,力图使三角学脱离天文学而成为一门独立的数学科目.他提出了正弦定理和正切定理,并用它们来解释三角形,但他没有实现他的愿望.真正使三角学成为一门独立的数学科目的学者是德国人约翰·米勒.
公元十五世纪,约翰·米勒以笔名列基蒙塔发表了第一本系统论述三角学的著作《论一般三角形》.该书全面地叙述了平面三角形和球面三角形的解法,并明确指出三角学是一门独立的数学科目,无需从属于天文学.
十六世纪,法国数学家韦达又将三角学进一步系统化,将三角学中的公式以拉丁字母来表示,从而使三角学具有了现代的形式.
十八世纪,欧拉给出了三角函数的概念,而原来意义下的正弦、余弦、正切、余切、正割、余割等概念,都可以脱离开几何图形来进行数学的推演,一切三角关系公式也很容易地从三角函数的定义出发而推导出来.欧拉的研究工作,使三角学从只是研究三角形的解法这一狭隘的天地中解放出来,使三角学有可能去研究现实世界中一切可以用三角函数来反映的运动和变化过程.因此,严格地说,此时才是三角学的真正的确定.欧拉应被推为三角函数近代理论的创始人.
笛卡尔在研究"解析几何"时创立的坐标方法,又一次推进了三角学的研究,为了研究任意角的三角函数,人们可以不再局限于直角三角形中用两边的比值来定义三角函数,也可以不象欧拉那样局限于圆中,认为“三角函数是一种函数线与圆半径的比值”,而是可以采用坐标方法来给出三角函数的定义,采用坐标方法来证明正弦定理、余弦定理,导出同角公式、诱导公式、和差公式,从而使三角学理论具有了更为广泛的、统一的形式.现行中学数学教材中,关于三角学的内容,就是采用这种统一的形式来编写的.
探究活动
课后有利用和(差)公式化简: 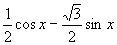 ,
,
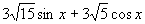 等习题,可以通过提出适当的数转化为一个角的三角函数形式
等习题,可以通过提出适当的数转化为一个角的三角函数形式
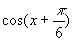 ,
,
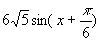 ,这里的系数都是些特殊数,提取后可以恰巧是某个特殊角的正弦或余弦.对于一般系数
,这里的系数都是些特殊数,提取后可以恰巧是某个特殊角的正弦或余弦.对于一般系数
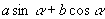 的形式能否也转化为一个角的三角函数形式呢?观察
的形式能否也转化为一个角的三角函数形式呢?观察
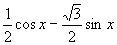 ,
,
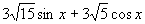 中提取的数与两个系数间的关系?能否利用观察的结果和两角和与差的三角函数将
中提取的数与两个系数间的关系?能否利用观察的结果和两角和与差的三角函数将
 ,通过提取适当的数系数转化为某个特殊角的正弦或余弦?另一个角如何确定?一般形式呢?
,通过提取适当的数系数转化为某个特殊角的正弦或余弦?另一个角如何确定?一般形式呢?
解:提取的数是两系数的平方和的算术平方根,所以  中提取
中提取
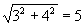 ,
,
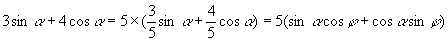
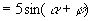 ,其中角
,其中角
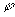 在第一象限,
在第一象限,
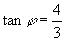 决定其大小.
决定其大小.
一般形式,如果能确定x与 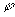 ,使
,使
 ,
,
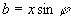 ,则原式
,则原式
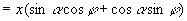 ,就能将原式转化为
,就能将原式转化为
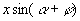 ,要满足上述条件要确定x与
,要满足上述条件要确定x与 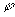 .由于
.由于
 ,可得
,可得
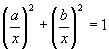 ,所以
,所以
 .因此
.因此
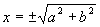 ,我们不妨取
,我们不妨取
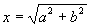 ,于是
,于是
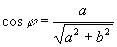 ,
,
 ,从而得
,从而得
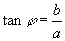 ,因为a,b是已知的,所以
,因为a,b是已知的,所以 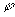 可以确定,原式转化为
可以确定,原式转化为
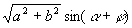 .
.
习题精选
[基础题]
(三)教学过程
1.已知 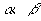 两角,我们可以利用
两角,我们可以利用
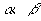 的三角函数去计算复合角
的三角函数去计算复合角
 的余弦,那么,我们能否用
的余弦,那么,我们能否用
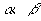 的三角函数去表达复合角
的三角函数去表达复合角
 的正弦呢?本节课将研究这一问题.
的正弦呢?本节课将研究这一问题.
2.探索研究
(1)请一位同学在黑板上写出  ,
,
 的展开式.
的展开式.
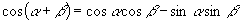
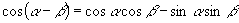 .
.
由于公式中的 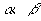 是任意实数,故我们对
是任意实数,故我们对
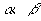 实施特值代换后并不影响等号成立,为此我们曾令
实施特值代换后并不影响等号成立,为此我们曾令
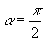 ,得到
,得到
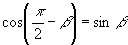 ,
,
 两个熟悉的诱导公式,请同学们尝试一下,能否在
两个熟悉的诱导公式,请同学们尝试一下,能否在
 中对
中对
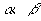 选取特殊实数代换,使
选取特殊实数代换,使
 诱变成
诱变成
 呢?或者说能否把
呢?或者说能否把
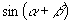 改成用余弦函数来表示呢?请同学回答.
改成用余弦函数来表示呢?请同学回答.
生:可以,因为 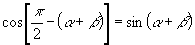
该同学的思路非常科学,这样就把新问题 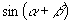 问题化归为老问题:
问题化归为老问题:
 .
.
事实上: 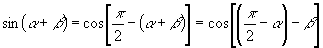 (视“
(视“  ”为
”为
 )
)


这样,我们便得到公式.
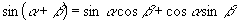 简化为
简化为
 .
.
由于公式中的 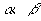 仍然是一切实数,请同学们再想一下,如何获得
仍然是一切实数,请同学们再想一下,如何获得
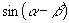 的展开式呢?请同学回答.
的展开式呢?请同学回答.
生:只要在公式  中用
中用
 代替
代替
 ,就可得到:
,就可得到:

即
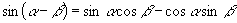
师:由此得到两个公式:
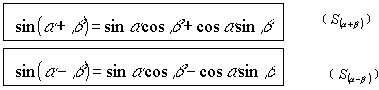
对于公式  还可以这样来推导:
还可以这样来推导:
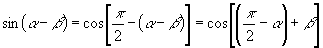
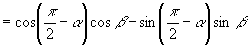

说明:
(1)上述四个公式 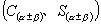 ,虽然形式、结构不同,但它们本质是相同的,因为它们同出一脉:
,虽然形式、结构不同,但它们本质是相同的,因为它们同出一脉:
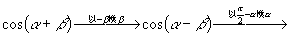


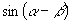
这样我们只要牢固掌握“中心”公式  的由来及表达方式,就掌握了其他三个公式了.这要作为一种数学思想、一个数学方法来仔细加以体会.
的由来及表达方式,就掌握了其他三个公式了.这要作为一种数学思想、一个数学方法来仔细加以体会.
(2) 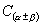 、
、
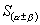 是用
是用
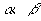 的单角函数表达复合角
的单角函数表达复合角
 的正、余弦.反之,我们不得不注意,作为公式的逆用,我们也可以用复合角
的正、余弦.反之,我们不得不注意,作为公式的逆用,我们也可以用复合角
 的三角函数来表达单角三角函数.诸如:
的三角函数来表达单角三角函数.诸如:
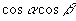 ,
,
 ,
,
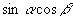 及
及
 四种表达式,实质上是方程思想的体现:
四种表达式,实质上是方程思想的体现:
由  得:
得:
 ①
①
由 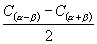 得
得
 ②
②
由 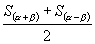 ,得:
,得:
 ③
③
由 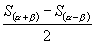 得:
得:
 ④
④
等式①、②、③、④在求值、证明恒等式中无疑作用是十分重大的.
(2)例题分析
[例1]
不查表,求  ,
,
 的值.
的值.
解: 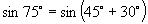
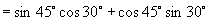

说明:我们也可以用 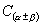 系统来做:
系统来做:

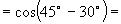
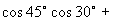

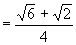
[例2]已知, 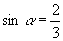 ,
,
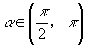 ,
,
 ,
,
 求,
求,
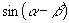 .
.
分析:观察公式  和本题的条件,必须先算出
和本题的条件,必须先算出
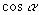 ,
,
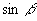
解:由 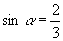 ,
,
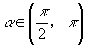 得
得

又由  ,
,
 得
得
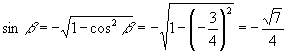
∴ 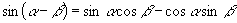
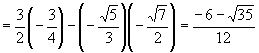
[例3]不查表求值:
(1) 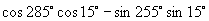 ;
;
(2) 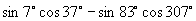 .
.
解:(1) 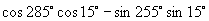

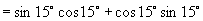
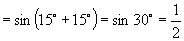
(2) 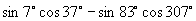

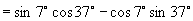


练习(投影)
(1)  ,
,
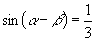 ,则
,则
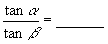 .
.
(2)在△ 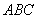 中,若
中,若
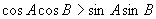 ,则△
,则△
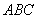 是___________.
是___________.
参考答案:
(1)∴ 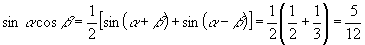

∴ 
(2)由 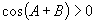 ,
,
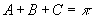
∴ 
∴ 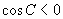 ,
,
 为钝角,即△
为钝角,即△
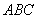 是钝角三角形.
是钝角三角形.
[例4]求证:  .
.
分析:我们从角入手来分析,易见左边有复角(即两角和与差)右边全是单角,所以思路明确,就是要把复角变单角.
证明:
左边 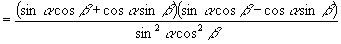
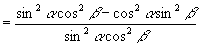
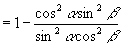
 右
∴原式成立
右
∴原式成立
如果我们本着逆用公式来看待本题,那么还可这样想:
由 
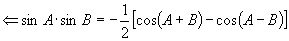
令  ,
,
 则
则
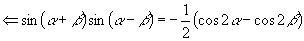 ①
①
至于 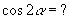

我们可这样分析:
∵ 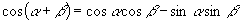
令 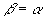 得
得


同理 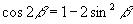
∴①可进一步改写为:
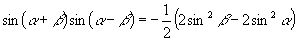
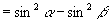
∴  ……②
……②
又∵

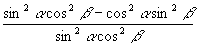
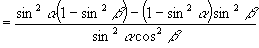
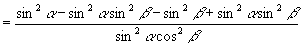
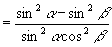 ……③
……③
由②、③得

本题还可以从函数名称来分析,左边是正、余弦函数,右边是正切函数,故可考虑从右边入手用化弦法,请同学们自己把上面过程反过来,从右边推出左边.
[例5]求证: 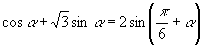
师:本题我们可以从角的形式来分析,左边是单角,右边是复角,如果从右边证左边则要把复角变单角(即利用和角公式);如果从左边证右边则须配一个角
 ,所以本题起码有两种证法.
,所以本题起码有两种证法.
证法1:右边 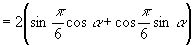
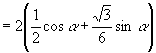
 左边
左边
∴原式成立
师:另一种证法根据刚才的分析要配出角  ,怎样配?大家仔细观察证法一就不难发现了.
,怎样配?大家仔细观察证法一就不难发现了.
证法2:(学生板书)
左边 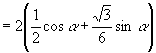
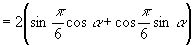
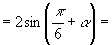 右边 ∴原式成立
右边 ∴原式成立
3.演练反馈(投影)
(1)化简 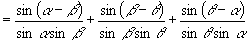
(2)已知  ,则
,则
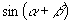 的值( )
的值( )
A.不确定,可在[0、1]内取值 B.不确定,可在[-1、1]中取值
C.确定,等于1 D.确定,等于1或-1
参考答案:
(1)原式

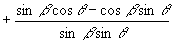
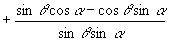

(2)C
4.总结提炼
(1)利用“拆角”“凑角”变换是进行三角函数式求值、证明、化简的常用技巧,如:
 ,
,
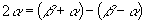 ,
,
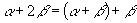 .在三角形中,
.在三角形中,
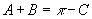 ,
,
 等变换技巧,同学们应十分熟悉.
等变换技巧,同学们应十分熟悉.
(2)本节课的例5,代表着一类重要题型,同学们要学习它的凑角方法,一般地  ,其中
,其中
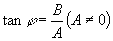 .
.
(3)在恒等式中,实施特值代换,是一类重要的数学方法--母函数法,这种方法在数学的其他学科中,均有用武之地。它反映的是特殊与一般的辨证统一关系.
(二)教学目标
1.掌握利用  得到的两角和与差的正弦公式.
得到的两角和与差的正弦公式.
2.运用 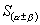 公式进行三角式的求值、化简及证明.
公式进行三角式的求值、化简及证明.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com