
(五)板书设计
|
课题 1.正、余弦函数线 2.作点 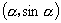 3.作 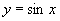 , ,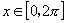 的图像 的图像4.五点法作正弦函数图像 |
5.变换法作 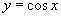 的图像 的图像6.五点法作余弦函数图像 7.例题 (1) (2) 演练反馈 |
总结提炼 |
教学设计示例
4.8 正弦函数、余弦函数的图像和性质(第二课时)
(二)教学目标
1.了解作正、余弦函数图像的四种常见方法.
2.掌握五点作图法,并会用此方法作出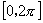 上的正弦曲线、余弦曲线.
上的正弦曲线、余弦曲线.
3.会作正弦曲线的图像并由此获得余弦曲线图像.
(一)教学具准备
直尺、圆规、投影仪.
参考答案: 1.A 2.C 3.C 4.C 5.A 6.D 7.C 8.C 9.C 10.A 11.B
12. 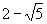 13.
13. 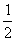 14.-1 15.2
14.-1 15.2
16.原式 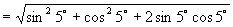
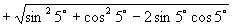
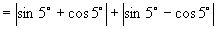
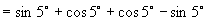
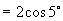 .
.
17.
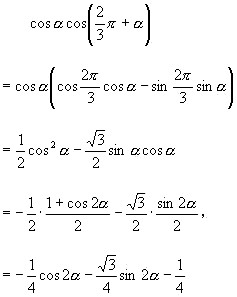
同理  ,
,
又 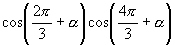
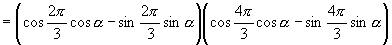
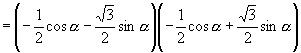
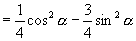
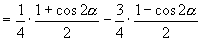
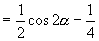 ,
,
于是原式 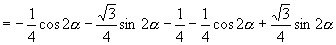
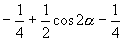
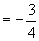 .
.
18.∵△ 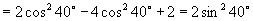 ,
∴
,
∴ 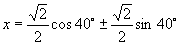 .
∴
.
∴  ,
,
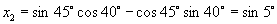 .
又由
.
又由 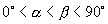 知
知
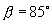 ,
,
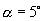 ,
∴
,
∴ 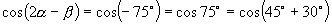
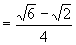 .
19.(1)
.
19.(1) 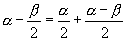 ,
,
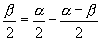 ,
∴左边展开再化正切,即得.
(2)∵
,
∴左边展开再化正切,即得.
(2)∵ 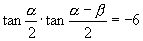 ,
,
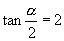 ,
∴
,
∴ 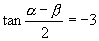 .
∴
.
∴ 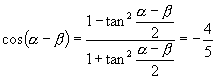 .
.
4.8正弦函数、余弦函数的图像和性质
教学目标
1.会用单位圆中的三角函数线画出正弦函数的图像,并在此基础上由诱导公式画出余弦函数的图像;
2.了解周期函数与最小正周期的意义,会求y=Asin(ωx+ψ)的周期,了解奇偶函数的意义,能判断函数的奇偶性;
3.通过正弦、余弦函数图像理解正弦函数、余弦函数的性质,培养学生的数形结合的能力;
4.简化正弦、余弦函数的绘制过程,会用“五点法”画出正弦函数、余弦函数和函数y=Asin(ωx+ψ)的简图;
5.通过本节的学习培养学生的化归能力、转化思想.
教学建议
知识结构:
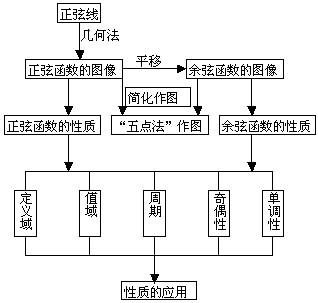
重点与难点分析:
本节重点是正弦函数、余弦函数的图像形状及其主要性质(定义域、值域、最值、周期性、奇偶性、单调性).正弦、余弦函数在实际生活中应用十分广泛,函数的图像和性质是应用的重要基础,也是解决三角函数的综合问题的基础,它能较好的综合三角变换的所有内容,可进一步深入研究其它函数的相关性质.函数图像可以直观的反映函数的性质,因此首先要掌握好函数图像形状特点,使学生将数、形结合对照掌握这两个函数.
本节难点是利用正弦线画出函数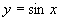
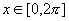 的图像,利用正弦曲线和诱导公式画出余弦曲线,周期函数与最小正周期意义的理解.利用几何法画函数图像学生第一次接触,要先复习正弦线的做法,另外注意讲清正弦线平移后在x轴上对应的角.通过诱导公式可以将正弦、余弦函数建立起关系,利用诱导公式时先将
的图像,利用正弦曲线和诱导公式画出余弦曲线,周期函数与最小正周期意义的理解.利用几何法画函数图像学生第一次接触,要先复习正弦线的做法,另外注意讲清正弦线平移后在x轴上对应的角.通过诱导公式可以将正弦、余弦函数建立起关系,利用诱导公式时先将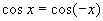 为了只需要平移就可得到余弦函数.周期函数包含的内容较多,可以先让学生通过正弦、余弦函数图像直观上了解,再通过定义严格说明,定义中x的任意性可与奇偶性的定义对比讲解,周期、最小正周期的概念很抽象,学生理解有些困难,最好将定义分解讲解.
为了只需要平移就可得到余弦函数.周期函数包含的内容较多,可以先让学生通过正弦、余弦函数图像直观上了解,再通过定义严格说明,定义中x的任意性可与奇偶性的定义对比讲解,周期、最小正周期的概念很抽象,学生理解有些困难,最好将定义分解讲解.
教法建议:
1.讲三角函数图象时,由于描点法学生比较熟悉,可以先让学生自己作图,然后介绍几何法,这样既可以让学生对正弦函数图像大致形状有所了解,为后面“五点法”作图奠定基础,又可将两种方法加以对比.
2.用几何法作函数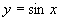
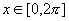 的图像前,首先复习函数线的作法,说明单位圆上的角与x轴上数值的对应关系,作图过程要力求准确,以便学生正确认识曲线的建立过程.此处最好借助多媒体课件演示,表现的既准确又节省时间.得到函数
的图像前,首先复习函数线的作法,说明单位圆上的角与x轴上数值的对应关系,作图过程要力求准确,以便学生正确认识曲线的建立过程.此处最好借助多媒体课件演示,表现的既准确又节省时间.得到函数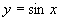
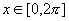 的图像,利用诱导公式或利用三角函数线,把图象沿着x轴向右和向左连续地平行移动,每次移动的距离为2π(即一个最小正周期),即可得到函数y=sinx,x∈R的图像.余弦函数的图像可以利用诱导公式将余弦与正弦建立联系,但要将x前面的系数保证为正,这样只需要平移即可得到余弦函数的图像.余弦函数的图像的几何作法可让学生课后自己去探索.
的图像,利用诱导公式或利用三角函数线,把图象沿着x轴向右和向左连续地平行移动,每次移动的距离为2π(即一个最小正周期),即可得到函数y=sinx,x∈R的图像.余弦函数的图像可以利用诱导公式将余弦与正弦建立联系,但要将x前面的系数保证为正,这样只需要平移即可得到余弦函数的图像.余弦函数的图像的几何作法可让学生课后自己去探索.
3.“五点法”作图在三角函数中应用较为广泛,让学生观察函数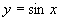
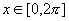 的图像,有五个点在确定图象形状时起着关键的作用,即最高点,最低点以及与x轴的交点,因为只要这五个点描出后,图象的形状就基本确定了.因此在精确度要求不太高时,常采用先描出这五个点来作函数简图的方法.适当增加些练习使学生熟练掌握这种方法.
的图像,有五个点在确定图象形状时起着关键的作用,即最高点,最低点以及与x轴的交点,因为只要这五个点描出后,图象的形状就基本确定了.因此在精确度要求不太高时,常采用先描出这五个点来作函数简图的方法.适当增加些练习使学生熟练掌握这种方法.
4.对于函数的周期性,先通过正弦、余弦函数图像的重复出现的特点,让学生对周期有直观的认识,周期函数的定义也可叙述为:当函数对于自变量的一切值每增加或减少一个定值(定值可以有很多个)、函数值就重复出现时,这个函数就叫做周期函数.然后再给出严格定义.将定义的分解讲解,使学生理解定义包含的要素,关键词语,如“如果存在”说明不是所有函数都有周期,“T”要满足“非零”和“常数”两个条件,当x取定义域内的每一个值时”这一提法,这里要特别注意“每一个值”四个字.如果函数f(x)不是当x取定义域内的“每一个值”时,都有f(x+T)=f(x),那么T就不是f(x)的周期.例如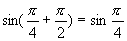 ,但是
,但是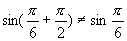 ,就是说
,就是说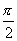 不能对于x在定义域内的每一个值都有
不能对于x在定义域内的每一个值都有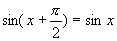 ,因此
,因此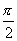 不是
不是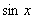 的周期.最小正周期可让学生按上述分析方法进行分析.另外可把三角函数和奇函数、偶函数象下面这样对比着进行讲解,对学生理解和掌握周期函数概念将是有益的:
的周期.最小正周期可让学生按上述分析方法进行分析.另外可把三角函数和奇函数、偶函数象下面这样对比着进行讲解,对学生理解和掌握周期函数概念将是有益的:
如果函数f(x)对于定义域里的每一个值,都有
(1)f(-x)=f(x),那么f(x)叫做偶函数;
(2)f(-x)=-f(x),那么f(x)叫做奇函数;
(3)f(x+T)=f(x),其中T是不为零的常数,那么f(x)叫做周期函数.
对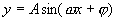 函数的周期,要让学生从周期定义上理解:周期是指能使函数值重复出现的自变量x要加上的那个数,这个数是针对x而言的,如果对2x而言,而每增加2π,sin2x的值就重复出现;但对自变量x而言,每增加π,sin2x的值就能重复出现,因此sin2x的周期是π.如果不设辅助未知数,本例的解答可写为:
函数的周期,要让学生从周期定义上理解:周期是指能使函数值重复出现的自变量x要加上的那个数,这个数是针对x而言的,如果对2x而言,而每增加2π,sin2x的值就重复出现;但对自变量x而言,每增加π,sin2x的值就能重复出现,因此sin2x的周期是π.如果不设辅助未知数,本例的解答可写为:
f(x)=sin2x=sin(2x+2π)=sin2(x+π)=f(x+π),
即f(x)中的x以x+π代替,函数值不变,所以sin2x的周期为π.由此可知,三角函数的周期与自变量x的系数有关.
5.让学生通过函数图像总结归纳函数的性质定义域、值域、极值、符号、周期性、奇偶性、单调性等,最好以表格的形式将正弦、余弦函数的性质对比得出,使学生在函数图像和性质建立对应关系,这对学生进一步掌握函数y=sinx,y=cosx的性质有很大帮助.因此应要求学生首先要熟悉正弦曲线和余弦曲线.
6.要注意数学语言和数学方法的训练,如“必须并且只需”,正弦函数在每一个闭区间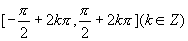 上都是增函数,其值从-1增大到1等.
上都是增函数,其值从-1增大到1等.
教学设计示例
4.8 正弦函数、余弦函数的图像和性质(第一课时)
11.化简 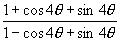 的值为( )
A.
的值为( )
A.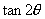 B.
B.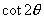 C.
C.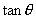 D.
D. 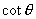
10.设 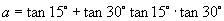 ,
,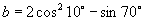 ,
,
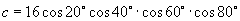 ,则( )
A.
,则( )
A.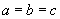 B.
B.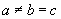 C.
C.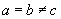 D.
D.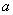 、
、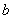 、
、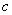 互不相等
互不相等
9.若 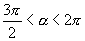 ,则
,则
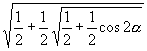 等于( )
A.
等于( )
A.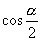 B.
B.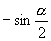 C.
C.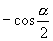 D.
D. 
8.如果 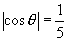 ,
,
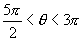 ,则
,则
 的值为( )
A.
的值为( )
A.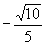 B.
B.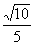 C.
C.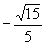 D.
D. 
7. 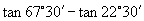 的值为( )
A.1
B.
的值为( )
A.1
B.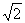 C.2 D.4
C.2 D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com