
9.函数 的图像相邻的两支截直线
的图像相邻的两支截直线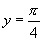 所得线段长为
所得线段长为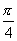 ,则
,则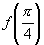 的值是( )
的值是( )
A.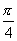 B.0 C.1 D.-1
B.0 C.1 D.-1
8.函数 的一个对称中心是( )
的一个对称中心是( )
A.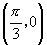 B.
B.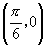 C.
C.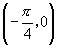 D.
D.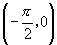
7.要得到 的图像,只需把
的图像,只需把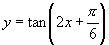 的图像( )
的图像( )
A.向左平移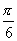 个单位 B.向左平移
个单位 B.向左平移 个单位
个单位
C.向右平移 个单位 D.向右平移
个单位 D.向右平移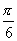 个单位
个单位
6.函数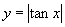 的图像对称于( )
的图像对称于( )
A.原点 B.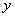 轴 C.
轴 C. 轴 D.直线
轴 D.直线
5.已知函数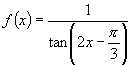 ,下列判断正确的个数是( )
,下列判断正确的个数是( )
①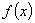 是定义域上的减函数,周期为
是定义域上的减函数,周期为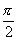 .
.
②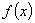 是区间
是区间 上的减函数,周期为
上的减函数,周期为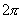 .
.
③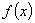 是区间
是区间 上的减函数,周期为
上的减函数,周期为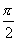 .
.
④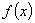 是区间
是区间 上的减函数,周期为
上的减函数,周期为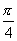 .
.
A.0 B.1 C.2 D.3
4.下列函数中,同时满足①在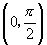 上是增函数;②为奇函数;③以
上是增函数;②为奇函数;③以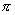 为最小正周期的函数是( )
为最小正周期的函数是( )
A.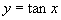 B.
B.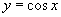 C.
C. D.
D.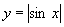
3.函数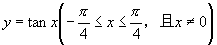 的值域是( )
的值域是( )
A.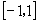 B.
B.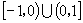 C.
C.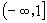 D.
D.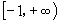
2.函数 的定义域是( )
的定义域是( )
A. B.
B.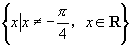
C.
D.
1.函数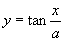 的最小正周期是( )
的最小正周期是( )
A. B.
B.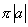 C.
C. D.
D.
(四)板书设计
|
课题-- 例1 例2 例3 例4 |
[参考例题] 演练反馈 总结提炼 |
典型例题
例1.比较下列各数大小:
(1)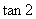 与
与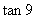 ;(2)
;(2)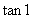 与
与 .
.
分析:同名函数比较大小时,应化为同一单调区间上两个角的函数值后,应用函数的单调性解决;而对于不同名函数,则应先化为同名函数再按上面方法求解.
解:(1)
因为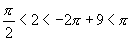 ,而
,而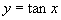 在
在 内是增函数
内是增函数
所以 , 即
, 即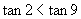
(2)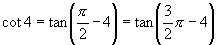

而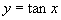 在
在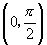 内是增函数,所以
内是增函数,所以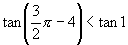
即 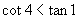
小结:比较两个三角函数值的大小,首先将函数名称统一,再利用诱导公式将角转化到同一个单调区间内,通过函数的单调性进行比较大小.
例2.求函数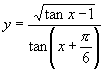 的定义域.
的定义域.
分析:根据自变量 满足的条例列出不等式组,解之即可.
满足的条例列出不等式组,解之即可.
解:由题得:
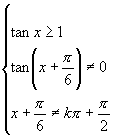

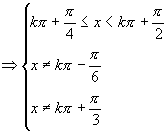
所以定义域为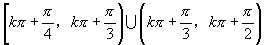 (
( ).
).
小结:注意不要忽略了正切函数存在的条件,本题中是 ,
, .
.
例3.(1)如图,函数 在一个周期内的图像是( )
在一个周期内的图像是( )
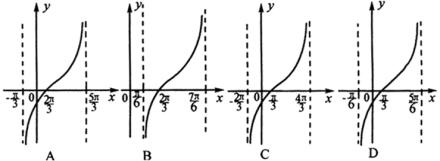
(2)要得到 的图像,只需将
的图像,只需将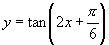 的图像( )
的图像( )
A.向左平移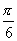 个单位 B.向右平移
个单位 B.向右平移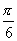 个单位
个单位
C.向左平移 个单位 D.向右平移
个单位 D.向右平移 个单位
个单位
分析:对于(1),可从周期、与 轴的交点等方面判断真假;对于(2),可将
轴的交点等方面判断真假;对于(2),可将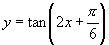 化成
化成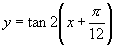 ,但要注意不是平移
,但要注意不是平移 的图像.
的图像.
解:(1)由函数表达式 知,这个函数的最小正周期为
知,这个函数的最小正周期为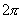 ,因此可排除
,因此可排除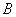 、
、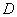 ,又函数表达式可化成
,又函数表达式可化成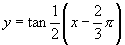 ,而这个函数的图像与函数
,而这个函数的图像与函数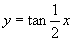 的图像形状相同,且将其向右侧平移
的图像形状相同,且将其向右侧平移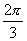 个单位.答案:A
个单位.答案:A
(2)因为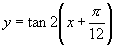 ,所以将其向右平移
,所以将其向右平移 个单位可得
个单位可得 的图像.答案:D
的图像.答案:D
小结:对于正切函数 (
(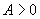 ,
,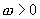 )的图像变换问题完全可比照正弦函数
)的图像变换问题完全可比照正弦函数 (
(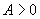 ,
,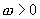 )的图像变换过程进行.
)的图像变换过程进行.
例4.作出函数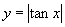 的图像,并根据图像求其单调区间.
的图像,并根据图像求其单调区间.
分析:要作出函数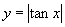 的图像,可先作出
的图像,可先作出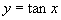 的图像,然后将它在
的图像,然后将它在 轴上方的图像保留,而将其在
轴上方的图像保留,而将其在 轴下方的图像向上翻(即作出关于
轴下方的图像向上翻(即作出关于 轴对称图像,)就可得到
轴对称图像,)就可得到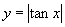 的图像.
的图像.
解:由于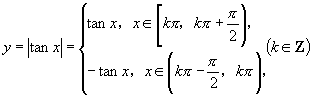
所以其图像如图所示,单调增区间为
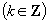 ;单调减区间为
;单调减区间为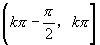
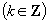 .
.

小结:利用正切函数的图象过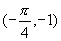
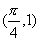 (0,0)三点且以
(0,0)三点且以 ,
,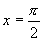 为渐近线,这样根据这三点两线就可以大体勾画出此图.再利用图象变换得到题目要求的图象,推导出函数性质.
为渐近线,这样根据这三点两线就可以大体勾画出此图.再利用图象变换得到题目要求的图象,推导出函数性质.
例5.求函数 的最小正周期.
的最小正周期.
分析:化简函数式半作出图形,再从图像上观察.
解:∵ (
(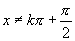 ,
, ),作出
),作出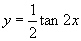 (
(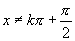 ,
, )的图像.
)的图像.
小结:求函数的周期通常有两种方法:转化为已知函数和图象观察,通过图象观察要注意图象草图尽量准确,尤其是定义域的范围.

从图像上面可以看出函数 的最小正周期为
的最小正周期为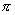 .
.
小结:在函数化简的过程中一定要注意函数的等价变换,尤其是要注意定义域.
扩展资料
《大衍历》的九服晷影算法及其正切函数表
我国古代历法从东汉《四分历》开始,就有各节气初日晷影长度和太阳去极度的观测记录,漏刻、晷影成为古代历法的重要计算项目。隋朝刘焯发明二次等间距插值法之后,李淳风首先将二次插值法引入到漏刻计算中,由每气初日的漏刻、晷影长度数求该气各日的漏刻、晷影数。但是,各历法中所记载和计算的漏刻和晷影大多是阳城(今河南登封东南告成镇)的数值。一行在编制《大衍历》时,曾进行了大规模的天文测量,通过观测知道,随去极度变化的影长,又因地方而异,但同太阳的天顶距有固定的对应关系。一行在《大衍历》中发明了求任何地方每日影长和去极度的计算方法,叫做“九服晷影”。
古人把阳城作为测影的标准地点,即所谓的地中。若NP为阳城的北极高度,S1、S2、S3……为阳城夏至、小暑、大暑等日的太阳上中天位置,则PS1、PS2、PS3……为阳城夏至、小暑、大暑……诸气太阳的去极度,取a1=PS2-PS1、a2=PS3-PS2……,则a1、a2分别为阳城夏至到小暑、小暑到大暑的去极度差数,也是太阳天顶距的差数。且这个差数对任何地点的相应季节都是相等的。
设有某地北极高度为NP′,则夏至、小暑、大暑等日的太阳上中天位置为S′1、S′2、S′3……。显然,有
a1=PS′2-PS′1,a2=PS′3-PS′2。
阳城夏至、小暑、大暑太阳天顶距为ZS1、ZS2、ZS3等,故
a1=ZS2-ZS1,a2=ZS3-ZS2,
同样,有
a1=ZS′2-ZS′2,a2=ZS′3-ZS′2。
历法中已给出阳城各气初日的太阳去极度,则各气的去极度差即为已知,同样各气的太阳天顶距差亦为已知,而这个差数对于任一地点都是相等的。这样一来,对于任一地方,只要知道某一节气(如夏至)的太阳天顶距,其他各气的太阳天顶距都可以通过加减这个差数求出。剩下还要解决以下两个问题:其一,如何求某地夏至(或冬至)的太阳天顶距;其二,已知天顶距如何换算出晷影长。这两个问题都可以通过建立一个影长与太阳天顶距的对应数表来解决。
如果列出一张以天顶距为引数,每隔一度的影长的数值表,则以上两个问题都可以解决:先在所测地测出(冬)夏至晷影长度(在一行领导的大地测量中,在每处都进行了这样的测量),由影长查表得出太阳天顶距,再加减一个如前所述的差数ai即可求出该地各气的天顶距,返回再查表得影长。一行在《大衍历》“步晷漏术”中就建立了这样一个从0度到80度的每度影长与太阳天顶距对应数表,这是世界数学史上最早的一张正切函数表。
在国外,大约920年左右,阿拉伯学者阿尔·巴坦尼(al-Battani,约858-929)根据影长与太阳仰角之间的关系,编制了0度-90度每隔一度时12尺竿子的影长表,这实际上是一个12ctga的数表。另一位阿拉伯学者阿尔·威发(Abul-Waha,940-998)在980年左右编成了正切和余切函数表,每隔15度和10度给出一个值。他还首次引进了正割和余割函数。一行和阿尔·巴坦尼差不多沿着相同的途径编成正切和余切函数表。一行用太阳天顶距,阿尔·巴坦尼用太阳仰角,两者互为余角,所以他们两人的发现是相同的。而一行的正切函数表比阿尔·巴坦尼的余切函数表早近两百年,比阿尔·威发的正切表要早二百五十年。尽管一行的正切函数表只从0度到80度,误差也相应大一些,但它毕竟是世界上最早的正切函数表。
探究活动
已知周期函数 的图象大致如下:当
的图象大致如下:当 时,
时,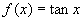 ,求
,求 在
在 上的解析式.
上的解析式.

解:当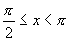 时,图象即
时,图象即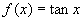 (
( )
)
向右平移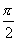 个单位,即
个单位,即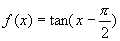 ;当
;当 时,图象即
时,图象即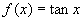 (
( )向右平移
)向右平移 个单位,即
个单位,即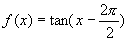 ;同理可得当
;同理可得当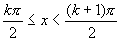 时,
时, ,(
,(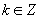 ),所以
),所以 ,(
,(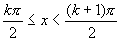 ,
,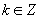 )
)
说明:这个问题的实质是图象的平移,关键是分区间找规律.
习题精选
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com