
1.求值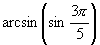 .
.
解:根据诱导公式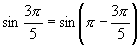 ,且
,且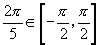 ,
,
∴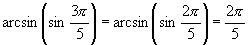 .
.
评法:由于反正弦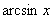 表示
表示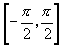 内的一个角,而
内的一个角,而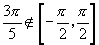 ,所以应先用诱导公式将其转化为区间
,所以应先用诱导公式将其转化为区间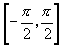 内的角,再进行计算.
内的角,再进行计算.
2.探索研究(此部分可由学生仿照正弦、余弦分析解决)
[例1](1)已知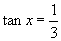 ,且
,且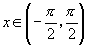 ,求
,求 (精确到
(精确到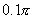 ).
).
(2)已知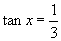 ,且
,且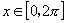 ,求
,求 的取值集合.
的取值集合.
解:(1)由正切函数在开区间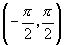 上是增函数和
上是增函数和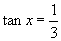 可知,符合条件的角有且只有一个,利用计算器可得
可知,符合条件的角有且只有一个,利用计算器可得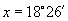 (或
(或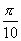 ).
).
(2)由正切函数的周期性,可知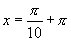 时,
时,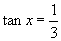 ,所以所求的
,所以所求的 的集合是
的集合是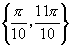 .
.
下面讨论反正切概念,请看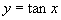 图形(图1)(投影仪):
图形(图1)(投影仪):
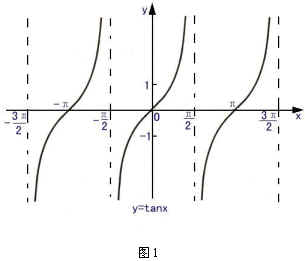
观察正切函数的图像的性质,为了使符合条件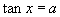 (
(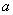 为任意实数)的角
为任意实数)的角 有且只有一个,我们选择开区间
有且只有一个,我们选择开区间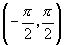 作基本的范围,在这个开区间内,符合条件
作基本的范围,在这个开区间内,符合条件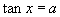 (
(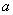 为任意实数)的角
为任意实数)的角 ,叫做实数
,叫做实数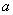 反正切,记作
反正切,记作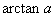 ,即
,即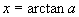 ,其中
,其中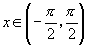 ,且
,且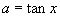 ,那么,此例第(2)小题的答案可以写成
,那么,此例第(2)小题的答案可以写成 .
.
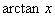 表示的意义:
表示的意义: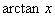 表示一个角,角的特点是①角的正切值为x,因此角的大小受x的限制;②并不是所有满足
表示一个角,角的特点是①角的正切值为x,因此角的大小受x的限制;②并不是所有满足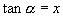 的角都可以,只能是
的角都可以,只能是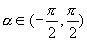 范围内满足
范围内满足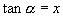 的角;③由于x为角的正切值,所以x的值可为全体实数.
的角;③由于x为角的正切值,所以x的值可为全体实数.
[例2](1)已知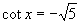 ,且
,且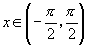 ,求
,求 .
.
(2)已知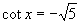 ,且
,且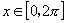 ,求
,求 的取值集合.
的取值集合.
解:(1)因为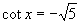 ,所以
,所以 .由正切函数在开区间
.由正切函数在开区间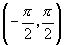 上是增函数可知符合条件的角有且只有一个,所以
上是增函数可知符合条件的角有且只有一个,所以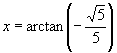 .
.
(2)由正切函数的周期性,可知当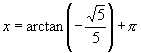 时,
时, .
.
∴所求 的取值集合是
的取值集合是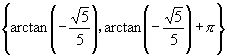 .
.
参考例题(供层次高的学生使用):
1.设置情境
师:请同学们看投影,回答问题
(1)若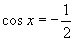 ,
,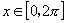 ,则
,则 .
.
(2)若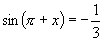 ,
,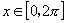 则
则 .
.
生:(1)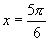 或
或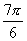 .
.
(2)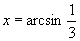 或
或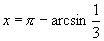 .
.
师:回答正确.请同学结合上面两个小题的求解过程,总结一下已知三角函数值求角的一般步骤:
生:从上面两个小题的求解过程看,有三个步骤:
第一步,决定角 可能是第几象限角.
可能是第几象限角.
第二步,如果函数值为正数,则先求出对应的锐角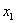 ;如果函数值为负数,则先求了与其绝对值对应的锐角
;如果函数值为负数,则先求了与其绝对值对应的锐角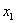 ;
;
第三步,如果函数值为负数,则根据角 可能是第几象限角,得出
可能是第几象限角,得出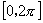 内对应的角-如果它是第二象限角,那么可表示为
内对应的角-如果它是第二象限角,那么可表示为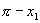 ,如果它是第三或第四象限角,那么可表示为
,如果它是第三或第四象限角,那么可表示为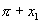 或
或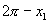 .
.
师:总结得很好,本节课我们继续学习用反正切表示角的方法,先请同学看问题(投影仪):
投影仪
2.掌握给定区间内,用反三角函数表示一个角的方法.
1.掌握已知一角的正切值,求角的方法.
|
课题 例1 反正弦概念 例2 |
反余弦概念 例3 用反三角函数表示角 |
演练反馈 总结提炼 |
教学设计示例(第二课时)
4.总结提炼
(1)反三角函数的概念是中学数学较难理解的概念之一,它之所以难以理解是由于三角函数在其整个定义域内并不存在反函数,只有在某一特定区间才存在反函数因此,反三角函数的值域也就被限制在某一区间内,这个区间常称为反三角函数的主值区间,如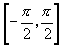 ,
,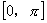 分别为反正弦、反余弦主值区间.解题出错,往往是主值区间概念不清.
分别为反正弦、反余弦主值区间.解题出错,往往是主值区间概念不清.
(2)由反正弦、反余弦定义,不难得:
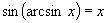 ,
,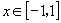
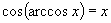 ,
,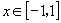
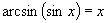 ,
,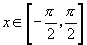
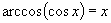 ,
,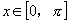
(3)用反三角表示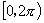 中角
中角
|
已知函数值 |
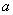 范围 范围 |
 值及位置 值及位置 |
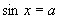 |
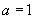 |
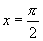 在 在 轴正半轴 轴正半轴 |
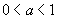 |
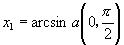 或 或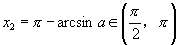 |
|
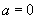 |
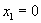 或 或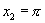 |
|
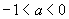 |
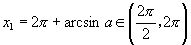 或 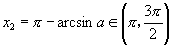 |
|
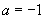 |
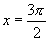 |
|
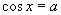 |
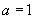 |
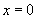 |
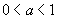 |
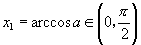 或 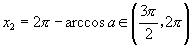 |
|
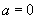 |
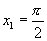 或 或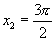 |
|
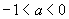 |
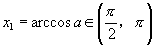 或 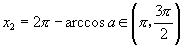 |
|
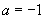 |
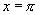 |
3.演练反馈(投影):
(1)若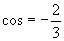 ,
,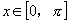 ,则
,则 的值为( )
的值为( )
A.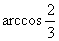 B.
B.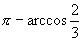 C.
C.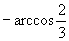 D.
D.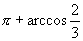
(2)若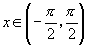 ,集合
,集合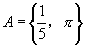 ,
,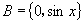 且
且 ,则
,则 的值为___________.
的值为___________.
(3)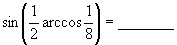 .
.
参考答案:
(1)B.说明: 应为钝角,故只有B.
应为钝角,故只有B.
(2)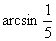 ,说明
,说明 ,只有
,只有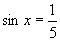 ,故
,故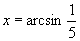
(3)∵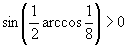
∴
2.探索研究
请同学回忆一下
(1)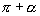 ,
,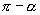 ,
,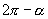 ,
,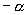 的诱导公式.
的诱导公式.
(2)师: ,
,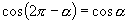 ,
,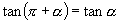 分别表示
分别表示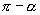 与
与 的正弦值相等,
的正弦值相等,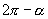 与
与 的余弦值相等,
的余弦值相等,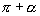 与
与 的正切值相等,能否说它们表示的角也相等?为什么?
的正切值相等,能否说它们表示的角也相等?为什么?
生:不能,因为在0- 间对一个已知的三角函数值一般都有两个角度与它对应.
间对一个已知的三角函数值一般都有两个角度与它对应.
师:对,同学们知道,利用诱导公式,我们可以求得任意角三角函数值,反过来,如果已知一个角的三角函数值,我们利用诱导公式也将能求出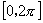 中与之对应的角.这两个过程是互逆的,已知角x求它的正弦值、余弦值、正切值是唯一的,而已知角的正弦值、余弦值、正切值求角在不同范围内可以是一个、二个,也可以是无数多个不同的解.
中与之对应的角.这两个过程是互逆的,已知角x求它的正弦值、余弦值、正切值是唯一的,而已知角的正弦值、余弦值、正切值求角在不同范围内可以是一个、二个,也可以是无数多个不同的解.
(板书课题--已知三角函数值求角(一))
请同学们看一个例题:
[例1](1)已知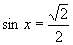 ,且
,且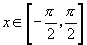 ,求
,求 .
.
(2)已知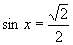 ,且
,且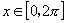 ,求
,求 的取值集合.
的取值集合.
师生共同分析:
(1)由正弦函数在闭区间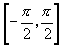 上是增函数和
上是增函数和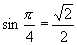 .可知符合条件的角有且只有一个,即
.可知符合条件的角有且只有一个,即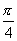 ,于是
,于是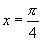 .
.
(2)因为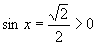 ,所以
,所以 是第一或第二象限角,由正弦函数的单调性和
是第一或第二象限角,由正弦函数的单调性和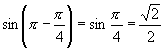 可知,符合条件的角有且只有两个,即第一象限角
可知,符合条件的角有且只有两个,即第一象限角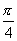 或第二象限角
或第二象限角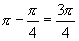 ,∴所求的
,∴所求的 的集合是
的集合是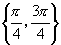 .
.
下面给出反正弦概念,请看投影:

观察上图,根据正弦函数的图像的性质,为了使符合条件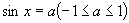 的角
的角 有且只有一个,我们选择闭区间
有且只有一个,我们选择闭区间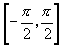 作为基本范围,在这个闭区间上,符合条件
作为基本范围,在这个闭区间上,符合条件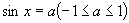 的角
的角 ,叫做实数
,叫做实数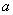 的反正弦,记作
的反正弦,记作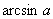 ,即
,即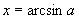 ,其中
,其中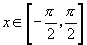 ,且
,且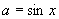 .
.
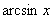 表示的意义:
表示的意义: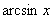 表示一个角,角的特点是①角的正弦值为x,因此角的大小受x的限制;②并不是所有满足
表示一个角,角的特点是①角的正弦值为x,因此角的大小受x的限制;②并不是所有满足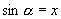 的角都可以,只能是
的角都可以,只能是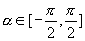 范围内满足
范围内满足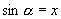 的角;③由于x为角的正弦值,所以x的值在[-1,1]范围内.
的角;③由于x为角的正弦值,所以x的值在[-1,1]范围内.
例如,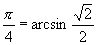 ,
,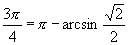 .那么例1中第(2)小题答案可以写成
.那么例1中第(2)小题答案可以写成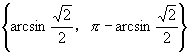 .
.
练习(投影)
(1)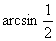 是什么意思?
是什么意思?
(2)若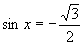 ,
,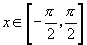 ,则
,则 .
.
(3)若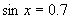 ,
,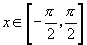 ,
, .
.
参考答案:
(1)表示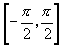 上正弦值等于
上正弦值等于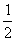 的那个角,其实应是
的那个角,其实应是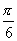 ,故记作
,故记作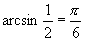
(2)这个 应该是
应该是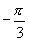 ,因此
,因此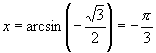
(3)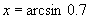 ,它不是特殊角,故只能这样抽象表示了.
,它不是特殊角,故只能这样抽象表示了.
下面再来建立反余弦概念.
先看下面例题:
[例2](1)已知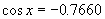 ,且
,且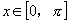 ,求
,求 ;
;
(2)已知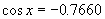 ,且
,且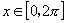 ,求
,求 的取值集合.
的取值集合.
师生共同分析:
解:(1)由余弦函数在闭区间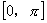 上是减函数和
上是减函数和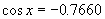 ,可知符合条件的角有且只有一个,这个角为钝角,利用计算器并由
,可知符合条件的角有且只有一个,这个角为钝角,利用计算器并由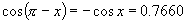 ,可得
,可得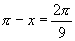 ,所以
,所以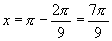 .
.
(2)因为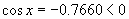 ,所以
,所以 是第二或第三象限角,由余弦函数的单调性和.
是第二或第三象限角,由余弦函数的单调性和.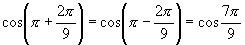
可知符合条件的角有且只有两个,即第二象限角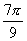 或第三象限角
或第三象限角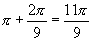 ,于是所求的
,于是所求的 的集合是
的集合是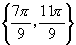 .
.
下面我们来给出反余弦定义,先看投影

观察上图,根据余弦函数图像的性质,为了使符合条件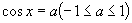 的角
的角 有且只有一个,我们选择闭区间
有且只有一个,我们选择闭区间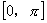 作为基本的范围,在这个闭区间上,符合条件
作为基本的范围,在这个闭区间上,符合条件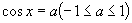 的角
的角 ,叫做实数
,叫做实数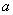 的反余弦,作
的反余弦,作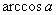 ,即
,即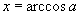 ,其中
,其中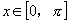 ,且
,且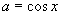 .
.
由学生根据反正弦的意义说明反余弦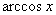 的意义:
的意义:
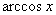 表示的意义:
表示的意义: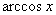 表示一个角,角的特点是①角的余弦值为x,因此角的大小受x的限制;②并不是所有满足
表示一个角,角的特点是①角的余弦值为x,因此角的大小受x的限制;②并不是所有满足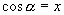 的角都可以,只能是
的角都可以,只能是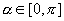 范围内满足
范围内满足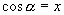 的角;③由于x为角的余弦值,所以x的值在[-1,1]范围内.
的角;③由于x为角的余弦值,所以x的值在[-1,1]范围内.
例如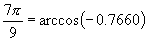
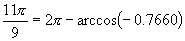
那么,例2的第(2)题的答案可以写成.
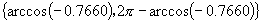
练习(投影)
(1)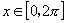 ,
,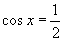 ,求
,求 ;
;
(2)已知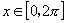 ,
,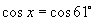 ,求
,求 ;
;
(3)已知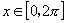 ,
, ,求
,求 .
.
参考答案:
(1)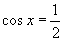 ,当
,当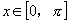 时,
时,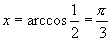 ;当
;当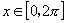 时,
时,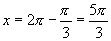 ,∴
,∴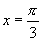 或
或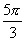 .
.
(2)∵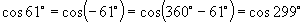 ,∴
,∴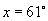 或
或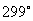
(3)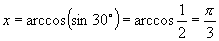 ,或
,或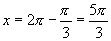 .
.
最后,我们来尝试用反三角表示角,请看投影.
[例3](1)已知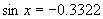 ,且
,且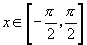 ,求
,求 (用弧度表示);
(用弧度表示);
(2)已知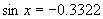 ,且
,且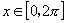 ,求
,求 的取值集合.
的取值集合.
解:(1)利用计算器并由
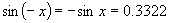
可得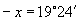 ,所以
,所以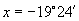 (或
(或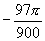 )也可写成
)也可写成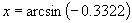
(2)由正弦函数的单调性和
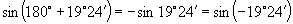

可知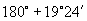 角,
角,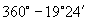 角的正弦值也是
角的正弦值也是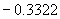 ,所以所求的
,所以所求的 的集合是
的集合是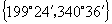 或
或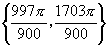
注:本例第(2)小题的结果实际上就是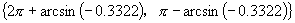
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com