
6.若 ,
, ,则
,则 等于( )
等于( )
A.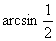 B.
B.
C. D.
D.
5.下列各结论正确的是( )
A.若 ,则
,则
B. ,则
,则
C.若 ,则
,则
D.若 ,则
,则 (其中
(其中 )
)
4.已知不等边△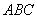 中,
中, ①
① ,②
,② ,③
,③ ,④
,④ 中可能成立的有( )
中可能成立的有( )
A.1个 B.2个 C.3个 D.4个
3.已知 ,
, ,则角
,则角 等于( )
等于( )
A.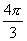 B.
B.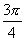 C.
C. D.
D.
2.已知 是三角形的内角,且
是三角形的内角,且 ,则角
,则角 等于( )
等于( )
A.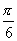 B.
B.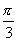 C.
C.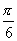 或
或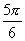 D.
D.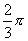 或
或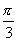
1.若 ,则角
,则角 为( )
为( )
A. ,
, B.
B. ,
,
C. ,
, D.
D. ,
,
|
课题 例1 例2 |
反正切 概念 |
演练反馈 总结提炼 |
典型例题
例1.已知 ,若(1)
,若(1) ;(2)
;(2) .求角
.求角
分析:由正切函数的单调性可知,在开区间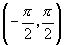 内,符合条件
内,符合条件 的角只有一个,而在
的角只有一个,而在 内,符号条件
内,符号条件 的角就有两个.
的角就有两个.
解 (1)由正切函数在开区间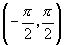 上是增函数可知;符合条件
上是增函数可知;符合条件 的角只有一个,即
的角只有一个,即 .
.
(2)∵ ,所以
,所以 是第二或第四象限角,
是第二或第四象限角,
又∵ ,由正切函数在区间
,由正切函数在区间 、
、 上是增函数知,符合
上是增函数知,符合 的角有两个.
的角有两个.
∵ ,且
,且 ,
,
∴ ,或
,或 .
.
小结:在某范围内解的个数判断,根据函数性质、三角函数线或三角函数值的符号判断所在象限,然后推广到整个范围.
例2.用反三角函数表示下列各式中的
(1) (
( );
);
(2) (
( );
);
(3) (
( );
);
(4) (
( ).
).
分析:用反三角函数表示角,应先观察题中的角是否在定义中规定的基本范围内,如在,则直接写出;如不在,则应运用诱导公式把角化入基本范围内.
解:(1)∵ ,∴
,∴ .
.
(2)∵ ,∴
,∴ .
.
由 ,即
,即 ,
,
∴ ,即
,即  .
.
(3)∵ ,∴
,∴ .
.
又 ,
,
∴ ,即
,即 .
.
(4)∵ ,∴
,∴ .
.
小结:利用反三角函数符号表示角要注意所能表示的范围:
 ,
,
 ,
,
 .
.
例3.已知 .
.
(1)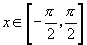 ,求
,求 ;
;
(2)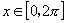 ,求
,求 的取值集合;
的取值集合;
(3) 时,求
时,求 的取值集合.
的取值集合.
分析:当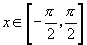 时,满足
时,满足 的
的 ,利用诱导公式可知满足
,利用诱导公式可知满足 且
且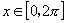 的
的 有两个值
有两个值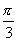 与
与 ,利用终边相同角的三角函数值相等可求出
,利用终边相同角的三角函数值相等可求出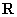 上的所有
上的所有 的集合.
的集合.
解:(1)由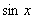 在
在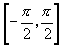 上是增函数及
上是增函数及 知,符合条件的角有且只有一个,利用反正弦概念得:
知,符合条件的角有且只有一个,利用反正弦概念得: .
.
(2)当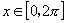 时,由诱导公式
时,由诱导公式 及
及 知
知 ,
, .于是所求的
.于是所求的 的集合是
的集合是 .
.
(3)当 时,根据正弦函数的周期性,可知当
时,根据正弦函数的周期性,可知当 或
或 ,
, 时,
时, .因此所求的
.因此所求的 的集合是
的集合是
 .
.
小结:(1)已知三角函数值求角,一般思路是先求出的给三角函数值的绝对值对应的锐角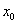 ,然后利用诱导公式求出
,然后利用诱导公式求出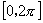 内的特解
内的特解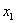 与
与 ,最后利用三角函数的周期性写出
,最后利用三角函数的周期性写出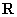 上的通解.
上的通解.
(2)本例是从不同的范围,阐述了已知三角函数值求角的方法,有很强的代表性,要认真领会,学会应用,若把正弦切成余弦、正切,也要会求.
例4.在一个正方形内作一个内接正方形,使这两个正方形面积之比为3:2,求内接正方形一边与原正方形一边之间所成的角.
分析:关键是设法将两正方形边之比表为其夹角 的函数,列出方程求解.
的函数,列出方程求解.
解:如图1,设正方形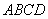 的内接正方形为
的内接正方形为 ,
, ,
, .则
.则


依题意有 
化简得: ,
,
即  .
.
∵ 为锐角,∴
为锐角,∴ 或
或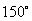 ,即
,即 或
或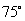 .
.
小结:将题目转化为已知三角函数值求角问题,在求解过程中尽量转化为一个角的三角函数形式,以便利用所学知识求解.
扩展资料
驾驭着波峰的数学

如果你是冲浪运动员,你知道有时难以预料何时浪会升起。有时浪在岸边完整地出现,但是当你进入水中时,它已经消失了,因此你就得等待完整波的到来,有时似乎要好几小时。在另外一些时候,完整波一个接一个地来到,可有许多个供你选择。不用说,波理论和波活动性是一个复杂的系统,许多因素影响着和创造着海浪。风、地震、船的尾波,当然还有月亮和太阳所产生的引起潮汐的万有引力,都扰动着海洋。海浪在水面上行动。当有多重的扰动或因素互相作用时,这些波动形式多少有点随机性。19世纪初,对海浪的数学开展了很多研究。在海上和在受控制的实验室中所作的观测,帮助科学家们获得了有趣的结论。1802年在捷克斯洛伐克,弗朗兹·格特纳开始提出最早的波理论。在他的观测中,他记录着波中水粒是如何作圆周运动的。位于波峰(最高点)的水的运动方向与波相同,位于波谷(最低点)的水的运动方向则相反。在水面上,每一水粒都沿着圆形轨道运动,然后回到原位。圆的直径被发现等于波的高度。水的整个深度中水粒都在生成圆。但水粒愈深,它的圆愈小。事实上,人们发现在相当于波长(两个相邻峰之间的水平距离)的1/9的深度,圆形轨道的直径大约是水面上水粒的圆形轨道的直径的一半。
因为波浪与这些作圆周运动的水粒有关,并且因为正弦曲线和摆线也与转动着的圆有关,这些数学曲线和它们的方程被用来描述海洋波浪就不奇怪了。但是人们发现,波浪既不是严格的正弦曲线,也不是任何别的纯粹的数学曲线。水的深度、风的强度和潮汐只是在描述波浪时必须考察的变量中的几个而已。今天研究波浪时,用到了概率、统计学和复杂性这些数学工具。人们考察了大量小波,并从所收集到的数据提出预测。
* * * * * *
海洋波浪的另外一些有趣的数学特性是:
(1)波长与周期有关。
(2)波高与周期和波长都无关(有一些例外,但周期和波长的影响很小)。
(3)当峰角超过120°时,波会破裂。波破裂时,它的大部分能量都消耗掉了。
(4)确定波何时将会破裂的另一方法是把波高与波长比较。当这比率大于1/7时,波将破裂。

波高 从峰到谷的垂直距离
波长 相邻两峰间的水平距离

波周期 波峰行经一个波长所需时间(以秒为单位)
正弦曲线是一种周期性(有规则地重复它的形状)的三角函数曲线。
摆线是指一个圆在一直线上平稳地滚动时圆上一定点的轨迹。

扩展资料
用几何画板巧作一段正切曲线
首先启用几何画板软件(如果您电脑上没有安装该软件,可以到网上免费下载,但4.0版的不免费),该画法分六步:
第一步:在图表菜单中选择建立直角坐标系命令,在图表菜单中选绘制点选项,绘制出点 、
、 、
、 .(
.( ,4.0以上版可以直接绘制点
,4.0以上版可以直接绘制点 )同时选点
)同时选点 、
、 轴(按住shift、下同),在作图菜单中选择平行线选项,做过
轴(按住shift、下同),在作图菜单中选择平行线选项,做过 点平行于
点平行于 轴的直线
轴的直线 ,同理可做出过
,同理可做出过 点的且平行于
点的且平行于 轴的直线
轴的直线 .
.
第二步:选择点 、点
、点 ,在作图菜单中选择“以圆心和圆周上的点画圆”选项,做出以
,在作图菜单中选择“以圆心和圆周上的点画圆”选项,做出以 为圆心,以线段
为圆心,以线段 为半径的圆,过
为半径的圆,过 点作出平行于
点作出平行于 轴的直线
轴的直线 ,选择圆和
,选择圆和 ,在作图菜单中选择“交点”选项,作出
,在作图菜单中选择“交点”选项,作出 与圆的交点
与圆的交点 、
、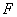 、隐藏
、隐藏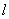 和圆,选择点
和圆,选择点 、
、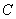 、
、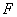 ,在作图菜单中选择“过三点的弧”选项,做出过
,在作图菜单中选择“过三点的弧”选项,做出过 、
、 、
、 三点的弧,连接点
三点的弧,连接点 、点
、点 、做出完整的半圆。
、做出完整的半圆。
第三步:选择“点”工具,在半圆上做出一个点 ,按照
,按照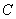 、
、 、
、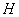 的顺序依次选择三个点,在“度量”菜单中选择“角度”选项,度量出
的顺序依次选择三个点,在“度量”菜单中选择“角度”选项,度量出 的大小,在“显示”菜单中选择“参数选择”选项,在对话框中把“角度”改为“弧度”,选择
的大小,在“显示”菜单中选择“参数选择”选项,在对话框中把“角度”改为“弧度”,选择 的度量值,在“图表”菜单中选择“绘制度量值”选项,出现绘制度量值对话框,单击“确定”,屏幕上出现一条垂直于
的度量值,在“图表”菜单中选择“绘制度量值”选项,出现绘制度量值对话框,单击“确定”,屏幕上出现一条垂直于 轴的虚线
轴的虚线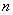
第四步:作出线段 ,在“作图”菜单中,做出过点
,在“作图”菜单中,做出过点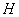 的线段
的线段 的垂线
的垂线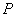 ,过
,过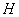 作
作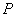 的垂直平分线
的垂直平分线 ,作出直线
,作出直线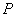 和直线
和直线 的交点
的交点 ,隐藏直线
,隐藏直线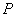 、
、 和线段
和线段 ,作出线段
,作出线段 ,过点工作直线
,过点工作直线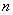 的垂线
的垂线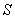 ,作出
,作出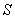 和
和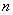 的交点
的交点 ,隐藏垂线
,隐藏垂线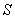 ,过点
,过点 、
、 作线段
作线段 ,选择
,选择 点,打开“显示”菜单选择“追踪点”选项,当点
点,打开“显示”菜单选择“追踪点”选项,当点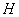 在半圆上运动时,点
在半圆上运动时,点 的轨迹就是正切图像。
的轨迹就是正切图像。
第五步:选择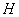 点和半圆,打开“编辑”菜单,选择“操作类按钮”选项,在下拉菜单中选择“动画”选项,在“匹配路径”对话框中,根据情况选择您所需要的动画,双击“动画”图标,点
点和半圆,打开“编辑”菜单,选择“操作类按钮”选项,在下拉菜单中选择“动画”选项,在“匹配路径”对话框中,根据情况选择您所需要的动画,双击“动画”图标,点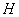 就自动地绕着半圆运动,此时点
就自动地绕着半圆运动,此时点 的轨迹就是正切
的轨迹就是正切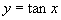 的一段图像
的一段图像
第六步:同时选择点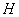 和点
和点 ,打开“作图”菜单,选择“轨迹”选项,正切和图像就出现了,选择正切图像,在“编辑”对话框中选择“操作类按钮”中的隐藏就可以根据您的需要显示或隐藏正切图像。
,打开“作图”菜单,选择“轨迹”选项,正切和图像就出现了,选择正切图像,在“编辑”对话框中选择“操作类按钮”中的隐藏就可以根据您的需要显示或隐藏正切图像。
探究活动
在实际使用计算机投影仪时,常常把投影仪的支架固定在天花板上,如图所示支架的末端P里投影中心O的距离为85.5英寸,俯角是 ,支架PE长18英寸,投影屏幕CD高(上沿与下沿的距离)6英尺,投影屏幕的厚度可以省略.(1英尺等于12英寸)
,支架PE长18英寸,投影屏幕CD高(上沿与下沿的距离)6英尺,投影屏幕的厚度可以省略.(1英尺等于12英寸)
(1)画出相关点与线的示意图,分别求出屏幕上沿和下沿D离天花板的距离.(精确到0.01英寸)
(2)求支架末端P分别与屏幕上沿和下沿连线的夹角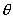 .
.
(3)若(2)中的 ,投影到屏幕上图形或文字会感到失真,如果把上沿C固定,将投影屏幕拉离墙面,那么当下沿
,投影到屏幕上图形或文字会感到失真,如果把上沿C固定,将投影屏幕拉离墙面,那么当下沿 与支架的末端P距离多少英寸时,可使
与支架的末端P距离多少英寸时,可使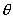 为
为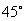 .
.

解:(1)示意图如图所示,设支架的末端为点P,支架在天花板上固定为点E,天花板和投影屏幕所在的墙的交点为点A,屏幕上沿、下沿、中心分别为C、D、O,过P作AD的垂线,垂足为点B,由题意,得
AB-EP=18,PO=85.5,CD=12×6=72,
CO=DO=36,∠BPO= .
.
在 中,
中, ,
,
所以BC=BO-CO=42.75-36=6.75
AC=AB+BC=24.75,
AD=AC+CD=96.75
所以屏幕上沿和下沿离天花板的距离分别为24.75英寸和96.75英寸.
(2)在 中,
中,
在 中,
中,
在 中,
中,

所以 ,即
,即 .
.
(3)设 ,在
,在 中,
中,
 ,
,
解得 或
或 (不符合实际意义,舍去).
(不符合实际意义,舍去).
所以下沿与支架的末端距离101.77英寸时,可使 .
.
习题精选
4.总结提炼
(1)由反正切定义知: ,
,
 ,
,
(2)已知: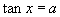 ,
, ,用
,用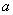 表示
表示
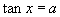 |
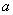 范围 范围 |
 位置及大小 位置及大小 |
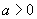 |
 或  |
|
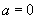 |
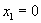 或 或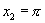 |
|
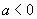 |
 或  |
3.演练反馈(投影)
(1)满足 的
的 的集合是( )
的集合是( )
A. B.
B.
C. D.
D.
(2)已知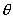 是第二象限角,是
是第二象限角,是 ,则
,则 .
.
(3)已知 ,
, ,且
,且 为第三象限角,
为第三象限角,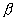 为第四象限角,求
为第四象限角,求 、
、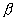 .
.
参考答案:
(1)D (2) ,
, .
.
(3)
∵ 为第三象限角,
为第三象限角,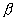 为第四象限角.
为第四象限角.
∴ ,
, ,
,
2.求 的值.
的值.
解:∵ 、
、 表示
表示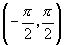 中的角
中的角
∴令 ,则
,则 ,
,
 ,则
,则
∴


又∵ 和
和 均为锐角
均为锐角
∴
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com