
3.未考点:等比数列考查较少(也考到),
思考:
◆等差(比)数列还能出怎样的好题?
◆09年的数列题给我们什么启示?
◆2010年的“示例”又说明什么?
◆简单的递推(可化为等差(比)的)是否会考?
|
7.基本不等式 |
|
|
√ |
|
一元二次不等式 |
|
|
√ |
|
线性规划 |
√ |
|
|
08考题11: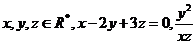 的最小值为 ▲
的最小值为 ▲
[解析]本题主要考查代数式的恒等变形及基本不等式等基础知识.本题属中等题.[答案]3.
09示例11.(08考题11)
2010示例11.(08考题11)
解析:不等式含2个C级考点,是高考的必考题型,
2.难度:中、难为主;
1.考法:以等差(比)数列为背景,考查代数论证能力、代数式的变形及运算能力;
10.(08考题)将全体正整数排成一个三角形数阵:
1
2 3
4 5 6
7 8 9 10
。 。 。 。 。
按照以上排列的规律,第n行(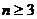 )从左向右的第3个数为
)从左向右的第3个数为
09示例7.已知数列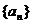 的前
的前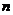 项和
项和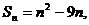 第
第 项满足
项满足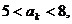 则
则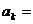
[解析]本题主要考查数列的前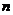 项的和与其通项的关系,以及解简单的不等式等基础知识.本题属中等题. [答案]6.
项的和与其通项的关系,以及解简单的不等式等基础知识.本题属中等题. [答案]6.
09考题14.设 是公比为
是公比为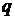 的等比数列,
的等比数列,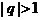 ,令
,令 若数列
若数列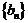 有连续四项在集合
有连续四项在集合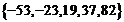 中,则
中,则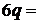 ★ .
★ .
2010示例(09示例7)
(08考题19)(1)设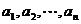 是各项均不为零的
是各项均不为零的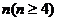 项等差数列,且公差
项等差数列,且公差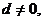
若将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,
(i)当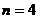 时,求
时,求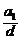 的数值;(ii)求
的数值;(ii)求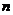 的所有可能值.
的所有可能值.
(2)求证:存在一个各项及公差均不为零的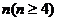 项等差数列,任意删去其中的
项等差数列,任意删去其中的 项
项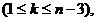 都不能使剩下的项(按原来的顺序)构成等比数列.
都不能使剩下的项(按原来的顺序)构成等比数列.
[解析]本题以等差数列、等比数列为平台,主要考查学生的探索与推理能力.本题属难题.(得分:3分)
09示例16.(08考题19)
09考题17.设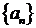 是公差不为零的等差数列,
是公差不为零的等差数列,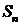 为其前
为其前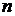 项和,满足
项和,满足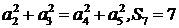
(1)求数列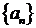 的通项公式及前
的通项公式及前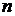 项和
项和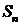 ;
;
(2)试求所有的正整数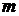 ,使得
,使得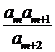 为数列
为数列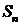 中的项.
中的项.
(得分:9.33分)
2010示例17. (08考题19)
解析:数列历来都是高考的热点,
3.未考点:向量的应用;
思考:
向量的数量积作为C级考点之一,理应着力考查,但由于内容的特殊性,在命题时常以“配角”身份出现,这种状况会不会有所改变?如何改变?会不会以向量作为“工具”,解决平面图形有关问题?(但这与“向量的应用A级”要求又不相符)
|
6.数列的概念 |
√ |
|
|
|
等差数列 |
|
|
√ |
|
等比数列 |
|
|
√ |
2.难度:易、中为主;
1.考法:小题主要围绕基向量间的运算(主要是数量积)命制;
解答题多与其它知识交汇,以向量形式呈现问题,通过向量
运算,还问题本来面貌;
3.未考点:概念、诱导公式、正切函数图像性质,小题注意!
思考:
◆2010年的示例是否意味着什么?
|
5.平面向量的概念 |
|
√ |
|
|
平面向量的加法、减法及数乘运算 |
|
√ |
|
|
平面向量的坐标表示 |
|
√ |
|
|
平面向量的数量积 |
|
|
√ |
|
平面向量的平行与垂直 |
|
√ |
|
|
平面向量的应用 |
√ |
|
|
(08考题5)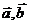 的夹角为
的夹角为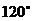 ,
,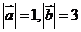 ,则
,则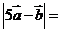
09示例8.已知向量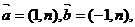 若
若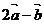 与
与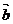 垂直,则
垂直,则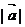 等于
等于
[解析]本题主要考查以坐标表示的平面向量的加、减、数乘及数量积的运算等基础知识.本题属中等题.[答案]2.
09考题2.已知向量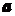 和向量
和向量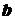 的夹角为
的夹角为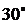 ,
, ,则向量
,则向量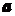 和向量
和向量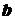 的数量积
的数量积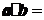 .
.
2010示例10:已知向量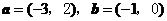 ,若
,若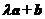 与
与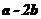 垂直,则实数
垂直,则实数 的值为________.
的值为________.
[解析]本题主要考查用坐标表示的平面向量的加减数乘及数量积的运算等基础知识,本题属中等题.[答案]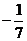
解析:平面向量是高考的必考点,其中含C级考点1个,B级考点4个!
2.难度:易、中难度为主;
1.考法:小题考查三角函数的图像性质+解答题考查三角恒等变换;或者:小题考查三角恒等变换+解答题考查解三角形;
或者:小题考查三角恒等变换+解答题考查三角应用题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com