
3.是否存在整数a,b,使函数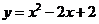 的定义域和值域均为区间[a,b]?如果存在,求出a,b;如果不存在,说明理由.
的定义域和值域均为区间[a,b]?如果存在,求出a,b;如果不存在,说明理由.
(用A4纸做,便于保存)
函数的单调性
复习目标:
1含参数的函数的单调性的讨论;
2.求函数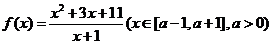 的最小值.
的最小值.
1.求函数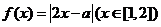 的值域.
的值域.
2.附加题部分
|
内 容 |
要 求 |
||||
|
A |
B |
C |
|||
选修系列 :不含选修系列 :不含选修系列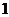 中的内容 中的内容 |
1.圆锥曲线 与方程 |
曲线与方程 |
√ |
|
大题:轨迹条件求抛物线的方程 |
|
顶点在坐标原点的抛物线的标准 方程与几何性质 |
|
√ |
|||
|
2.空间向量 与立体几何 |
空间向量的概念 |
√ |
|
大题:运用空间向量求空间角(尤其是二面角)、探索线面垂直的条件 |
|
|
空间向量共线、共面的充分必要条件 |
|
√ |
|||
|
空间向量的加法、减法及数乘运算 |
|
√ |
|||
|
空间向量的坐标表示 |
|
√ |
|||
|
空间向量的数量积 |
|
√ |
|||
|
空间向量的共线与垂直 |
|
√ |
|||
|
直线的方向向量与平面的法向量 |
|
√ |
|||
|
空间向量的应用 |
|
√ |
|||
|
3.导数及其 应用 |
简单的复合函数的导数 |
|
√ |
大题:不太可能单独考 |
|
|
定积分 |
√ |
|
|||
|
4.推理与 证明 |
数学归纳法的原理 |
√ |
|
大题:运用数学归纳法证明有关问题(归纳、猜想、证明)(要重视) |
|
|
数学归纳法的简单应用 |
|
√ |
|||
|
5.计数原理 |
加法原理与乘法原理 |
|
√ |
大题:不太可能再考 |
|
|
排列与组合 |
|
√ |
|||
|
二项式定理 |
|
√ |
|||
|
6.概率、统计(删去A级考点:统计案例(独立性检验、回归分析)) |
离散型随机变量及其分布列 |
√ |
|
大题: 离散型随机变量的分布列、均值与方差 |
|
|
超几何分布 |
√ |
|
|||
|
条件概率及相互独立事件 |
√ |
|
|||
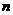 次独立重复试验的模型及二项分布 次独立重复试验的模型及二项分布 |
|
√ |
|||
|
离散型随机变量的均值与方差 |
|
√ |
|||
|
下面探讨2010年的备考策略,见ppt. 2010年高考复习讲座 jb |
|||||
|
内容 |
要求 |
||||
|
A |
B |
C |
|||
选修系列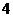 中 中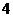 个专题 个专题
|
7.几何证明 选讲 |
相似三角形的判定与性质定理 |
|
√ |
|
|
射影定理 |
√ |
|
|
||
|
圆的切线的判定与性质定理 |
|
√ |
|
||
|
圆周角定理,弦切角定理 |
|
√ |
|
||
|
相交弦定理、割线定理、切割线定理 |
|
√ |
|
||
|
圆内接四边形的判定与性质定理 |
|
√ |
|
||
|
8.矩阵与变换(常见的平面变换由B级降为A级) |
矩阵的概念 |
√ |
|
|
|
|
二阶矩阵与平面向量 |
|
√ |
|
||
|
常见的平面变换 |
√ |
|
|
||
|
矩阵的复合与矩阵的乘法 |
|
√ |
|
||
|
二阶逆矩阵 |
|
√ |
|
||
|
二阶矩阵的特征值与特征向量 |
|
√ |
|
||
|
二阶矩阵的简单应用 |
|
√ |
|
||
|
9.坐标系与 参数方程 |
坐标系的有关概念 |
√ |
|
|
|
|
简单图形的极坐标方程 |
|
√ |
|
||
|
极坐标方程与直角坐标方程的互化 |
|
√ |
|
||
|
参数方程 |
|
√ |
|
||
|
直线、圆及椭圆的参数方程 |
|
√ |
|
||
|
参数方程与普通方程的互化 |
|
√ |
|
||
|
参数方程的简单应用 |
|
√ |
|
||
|
10.不等式选讲 |
不等式的基本性质 |
|
√ |
|
|
|
含有绝对值的不等式的求解 |
|
√ |
|
||
|
不等式的证明(比较法、综合法、分析法) |
|
√ |
|
||
|
算术-几何平均不等式与柯西不等式 |
√ |
|
|
||
|
利用不等式求最大(小)值 |
|
√ |
|
||
|
运用数学归纳法证明不等式 |
|
√ |
|
1.必做题部分
|
内 容 |
要 求 |
|||
|
A |
B |
C |
||
|
1.集合 |
集合及其表示 |
√ |
|
小题:集合的并、补集 |
|
子集 |
|
√ |
||
|
交集、并集、补集 |
|
√ |
||
|
2.函数概念 与基本初 等函数Ⅰ |
函数的概念 |
|
√ |
小题:一般函数(或对数函数)的性质; 解答题:运用导数(转化为二次函数)研究函数(含 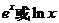 )的性质 )的性质 |
|
函数的基本性质 |
|
√ |
||
|
指数与对数 |
|
√ |
||
|
指数函数的图象与性质 |
|
√ |
||
|
对数函数的图象与性质 |
|
√ |
||
|
幂函数 |
√ |
|
||
|
函数与方程 |
√ |
|
||
|
函数模型及其应用 |
|
√ |
||
|
3.基本初等 函数Ⅱ(三角函数)、三角恒等变换 |
三角函数的概念 |
|
√ |
小题:诱导公式+同角三角函数;解答题:解三角形+恒等变换+函数值域 |
|
同角三角函数的基本关系式 |
|
√ |
||
|
正弦函数、余弦函数的诱导公式 |
|
√ |
||
|
正弦函数、余弦函数、正切函数的图象与性质 |
|
√ |
||
函数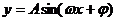 的图象与性质 的图象与性质 |
√ |
|
||
|
两角和(差)的正弦、余弦及正切(C) |
|
|
||
|
二倍角的正弦、余弦及正切 |
|
√ |
||
|
积化和差、和差化积及半角公式 |
√ |
|
||
|
4.解三角形 |
正弦定理、余弦定理及其应用 |
|
√ |
|
|
5.平面向量 |
平面向量的概念 |
|
√ |
小题:由向量的平行与垂直确定参数的值或向量数量积的运算; 解答题:其它知识戴向量帽子或单独考向量在几何图形中的运用 |
|
平面向量的加法、减法及数乘运算 |
|
√ |
||
|
平面向量的坐标表示 |
|
√ |
||
|
平面向量的数量积(C) |
|
|
||
|
平面向量的平行与垂直 |
|
√ |
||
|
平面向量的应用 |
√ |
|
||
|
6.数列 |
数列的概念 |
√ |
|
|
|
等差数列(C) |
|
|
小题:等差(比)的基本量的运算或简单性质的运用; 解答题:等差(比)数列的判断与性质的推证 |
|
|
等比数列(C) |
|
|
||
|
7.不等式 |
基本不等式 |
|
|
小题:运用基本不等式求函数(二元或一元分式)的最值;也可能考查线性规划; 解答题:与其它知识综合考查 |
|
一元二次不等式 |
|
|
||
|
线性规划 |
√ |
|
||
|
8.复数 |
复数的概念 |
|
√ |
小题:复数的概念和四则运算; |
|
复数的四则运算 |
|
√ |
||
|
复数的几何意义 |
√ |
|
||
|
9.导数及其应用 |
导数的概念 |
√ |
|
小题:切线、单调性、极值的基本运算; 解答题:代数论证压轴题;也可能是中档计算与推证题(见示例) |
|
导数的几何意义 |
|
√ |
||
|
导数的运算 |
|
√ |
||
|
利用导数研究函数的单调性与极值 |
|
√ |
||
|
导数在实际问题中的应用 |
|
√ |
||
|
10.算法初步(“概念”改为“含义”) |
算法的含义 |
√ |
|
小题:流程图+数列求和的小题; |
|
流程图 |
√ |
|
||
|
基本算法语句 |
√ |
|
||
|
11.常用逻辑用语 |
命题的四种形式 |
√ |
|
小题:量词构成的命题为真判断或充要条件的判断 |
|
充分条件、必要条件、充分必要条件 |
|
√ |
||
|
简单的逻辑联结词 |
√ |
|
||
|
全称量词与存在量词 |
√ |
|
||
|
12.推理与证明 |
合情推理与演绎推理 |
|
√ |
小题:归纳结论 |
|
分析法与综合法 |
√ |
|
||
|
反证法 |
√ |
|
||
|
13.概率、统计 |
抽样方法 |
√ |
|
小题:运用频率求样本均值,或简单的分层抽样的运算 |
|
总体分布的估计 |
√ |
|
||
|
总体特征数的估计 |
|
√ |
||
|
变量的相关性 |
√ |
|
||
|
随机事件与概率 |
√ |
|
小题、解答题:古典概型的计算 |
|
|
古典概型 |
|
√ |
||
|
几何概型 |
√ |
|
||
|
互斥事件及其发生的概率 |
√ |
|
||
|
14.空间几何体 (删去A级考点:三视图与直观图) |
柱、锥、台、球及其简单组合体 |
√ |
|
小题:简单集合体的面、体积的计算 |
|
柱、锥、台、球的表面积和体积 |
√ |
|
||
|
15.点、线、面 之间的位置关系 |
平面及其基本性质 |
√ |
|
解答题:线面平行、垂直的证明;面面垂直的证明 |
|
直线与平面平行、垂直的判定及性质 |
|
√ |
||
|
两平面平行、垂直的判定及性质 |
|
√ |
||
|
16.平面解析 几何初步 |
直线的斜率和倾斜角 |
|
√ |
小题: ◆直线的平行与垂直的条件; ◆求直线或圆的方程; ◆直线和圆的位置关系判断; ◆已知位置关系、数量关系确定相关参数的值(范围)(不单独考解答题) |
|
直线方程(C) |
|
|
||
|
直线的平行关系与垂直关系 |
|
√ |
||
|
两条直线的交点 |
|
√ |
||
|
两点间的距离、点到直线的距离 |
|
√ |
||
|
圆的标准方程与一般方程(C) |
|
|
||
|
直线与圆、圆与圆的位置关系 |
|
√ |
||
|
空间直角坐标系 |
√ |
|
||
|
17.圆锥曲线与方程 |
中心在坐标原点的椭圆的标准方程与几何性质 |
|
√ |
小题:曲线(含双曲线、抛物线)基本量的计算 解答题: ◆建立椭圆基本量的方程组(或轨迹条件)求其方程; ◆椭圆简单的几何性质的推证; ◆以圆等其它曲线为背景考查椭圆 |
|
中心在坐标原点的双曲线的标准方程与几何性质 |
√ |
|
||
|
顶点在坐标原点的抛物线的标准方程与几何性质 |
√ |
|
3.未考点:共轭复数、复数的几何意义(模、向量表示)
思考:复数考题题型会不会有所改变?如何改变?
|
9.导数及其应用 |
导数的概念 |
√ |
|
|
|
导数的几何意义 |
|
√ |
|
|
|
导数的运算 |
|
√ |
|
|
|
利用导数研究函数的单调性与极值 |
|
√ |
|
|
|
导数在实际问题中的应用 |
|
√ |
|
(08考题8)直线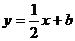 是曲线
是曲线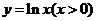 的一条切线,则实数b的值为 ▲
的一条切线,则实数b的值为 ▲
[解析]本题主要考查导数的几何意义,切线的求法,本题属于中等题.[答案]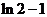 .
.
(08考题14)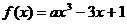 对于
对于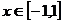 总有
总有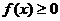 成立,则
成立,则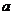 =
▲
=
▲
09示例15.设函数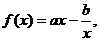 曲线
曲线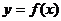 在点
在点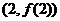 处的切线方程为
处的切线方程为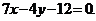
(1)求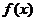 的解析式;
的解析式;
(2)证明:曲线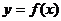 上任一点处的切线与直线
上任一点处的切线与直线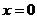 及直线
及直线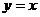 所围成的三角形的面积是一个(与
所围成的三角形的面积是一个(与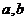 无关的)定值,并求此定值.
无关的)定值,并求此定值.
[解析]本题主要考查导数的几何意义、导数的运算以及直线方程等基础知识,考查运算求解能力、推理论证能力.本题属中等题.
2.难度:易
1.考法:复数的四则运算(以乘除法运算为主)+复数的概念(实虚部、相等)
3.未考点:线性规划
思考:
◆会不会考“线性规划”?
◆09年应用题考查了求形如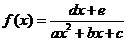 的分式函数的最值,通过多项式的除法运算,可化归为形如
的分式函数的最值,通过多项式的除法运算,可化归为形如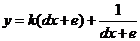 型函数,运用基本不等式求解,这类“陈题”会否再考?
型函数,运用基本不等式求解,这类“陈题”会否再考?
◆08考题11连续作为09、10典型题示例,这意味着什么?
|
8.复数 |
复数的概念 |
|
√ |
|
|
复数的四则运算 |
|
√ |
|
|
|
复数的几何意义 |
√ |
|
|
(08考题3)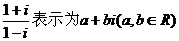 的形式,则
的形式,则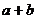 =
=
09示例3.若将复数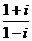 表示为
表示为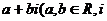 是虚数单位)的形式,则
是虚数单位)的形式,则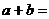
[解析]本题主要考查复数的运算.本题属容易题.[答案]l.
09考题1.若复数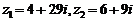 ,其中
,其中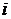 是虚数单位,则复数
是虚数单位,则复数 的实部为★.
的实部为★.
2010示例3.若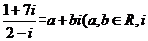 是虚数单位),则乘积
是虚数单位),则乘积 的值是
的值是
[解析]本题主要考查复数的基本概念,本题属于容易题.[答案]-3
解析:复数这一内容如同鸡肋,“弃之可惜,考之无味”
1.考法:小题既可单独考查,也可与其它知识交汇考查;解答题一般
不会单独考,常常与“函数”、“数列”等其它知识综合考查;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com