4.已知函数．若时，恒有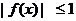, 试求实数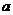的取值范围.

§9　　 简单的有理函数与无理函数

复习目标：

3.已知函数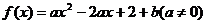，在区间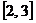上有最大值5，最小值2，求a，b的值。

2.函数f(x)=x²+ax+3，当x∈[－2,2]时，f(x)≥a恒成立，求a的取值范围.

1.已知二次函数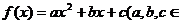R)满足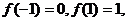且对任意实数x都有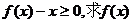的解析式.

2.准确的作出所给函数的示意图，能帮助我们理解题意，找准分类标准，但解题过程中应结合图像对函数的性质作适当的描述，以提高解题的严谨性

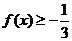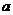变式3：(自编)设，在区间 [1，2]上，有，求的取值范围

答案：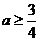

说明：此类不等式恒成立问题，有两种转化方向：

(1)转化为含参数的函数的最值问题(或范围问题)；

(2)分离参数后，转化为一个已知函数的最值(或范围)问题

(3)上述两种转化都能进行时，一般说来，分离参数法更为简单.

练习：(自编)设函数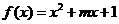同时满足下列条件：

(1)对一切实数，；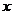

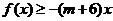(2)当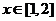时，.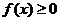

求实数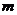的取值集合.

答案：

课后补充作业：

2.二次函数、二次不等式之间关系的运用；

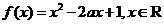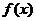题1：设，求函数在区间

[1，2]上的最小值，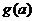

答案：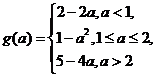

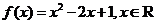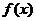变式1：设，求函数在区间

[a，a+1]上的最小值，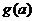

答案：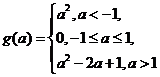

说明：抓住指定区间和二次函数图象的对称轴的相对位置是解好问题的关键

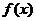变式2：设，求函数在区间

[1，2]上的最小值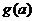

答案：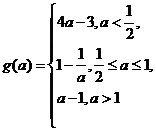

说明：1.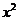的系数含参量a时，一方面要注意的特殊情形，另一方面要注意a为负的情形

1.含参数的二次函数的最值问题的讨论；

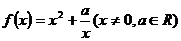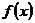3.已知函数，若在区间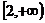是增函数，求实数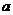的取值范围。

二次函数补充题

复习目标：

2.函数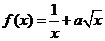在区间(0，4]上单调递减，求a的取值范围．

2. 给定函数在指定区间上的单调性，求参数的范围.

例1：已知，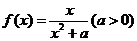

(1)试判断函数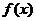的单调性；

(2)求函数f(x)在区间［1，2］上的最大值.

例2：设函数f(x)=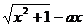,求a的取值范围，使函数f(x)在区间[1,2]上是单调递增函数

例3：已知f(x)=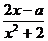在区间[-1，1]上是增函数，求实数a的值组成的集合.

作业：

1：设函数f(x)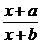＝(a＞b＞0)，讨论f(x)的单调区间.