
4.已知θ是第二象限的角,且sin4θ+cos4θ=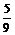 ,求sin2θ
,求sin2θ
3. 已知 ,且
,且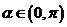 ,求下列各式的值:①sin3α+cos3α; ②sin4α+cos4α
,求下列各式的值:①sin3α+cos3α; ②sin4α+cos4α
2.已知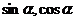 是方程
是方程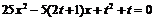 的两根且
的两根且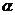 为锐角,求t的值.
为锐角,求t的值.
1.解不等式: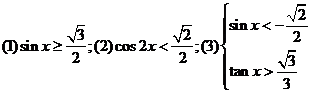
3. 公式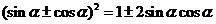 的运用.
的运用.
专题1:单位圆中的三角函数线的运用
例1:解不等式: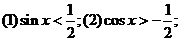 (3)
(3)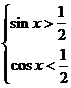
例2:(2000全国,4)已知sinα>sinβ,那么下列命题成立的是( )
A.若α、β是第一象限角,则cosα>cosβ B.若α、β是第二象限角,则tanα>tanβ
C.若α、β是第三象限角,则cosα>cosβ D.若α、β是第四象限角,则tanα>tanβ
专题2: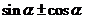 的符号确定方法及其运用
的符号确定方法及其运用
例3:(2007辽宁理5)若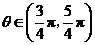 ,则复数
,则复数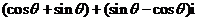 在复平面内所对应的点在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限
在复平面内所对应的点在( )A.第一象限 B.第二象限 C.第三象限 D.第四象限
例4:(2002春北京、安徽)若角α满足条件sin2α<0,cosα-sinα<0,则α在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
例5:(1998全国,6)已知点P(sinα-cosα,tanα)在第一象限,则在[0,2π]内α的取值范围是( )
A.(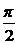 ,
,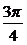 )∪(π,
)∪(π,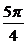 ) B.(
) B.(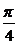 ,
,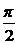 )∪(π,
)∪(π,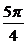 )
)
C.(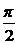 ,
,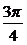 )∪(
)∪(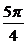 ,
,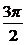 ) D.(
) D.(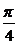 ,
,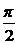 )∪(
)∪(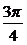 ,π)
,π)
例6:已知q为第二象限角,且sin<cos,那么sin+cos的取值范围是( )
A. ( -1 ,0 ) B. ( 1 ,) C. ( -1 ,1 ) D. ( - ,-1 )
专题3:公式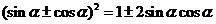 的运用
的运用
例7:若
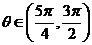 ,求:
,求: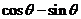 、
、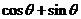 的值
的值
例8:已知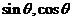 是方程
是方程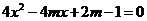 的两个根,
的两个根,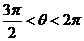 ,求角
,求角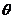 .
.
例9:求函数y=sinxcosx+sinx+cosx的最大值和最小值
课后练习:
1.单位圆中的三角函数线的运用;2. 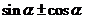 的符号确定方法及其运用;
的符号确定方法及其运用;
14. (06重庆卷)已知定义域为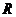 的函数
的函数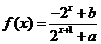 是奇函数。
是奇函数。
(Ⅰ)求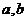 的值;
的值;
(Ⅱ)若对任意的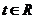 ,不等式
,不等式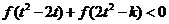 恒成立,求
恒成立,求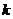 的取值范围;
的取值范围;
点评:注意不等式恒成立问题的处理方法!
平面向量的几何运算、式的运算补充问题
复习目标:
1:用基底表示指定的向量;
解题关键:设 ,学会通过运算求得
,学会通过运算求得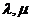 的值
的值
2:会根据向量条件,确定点P的位置.
解题关键:寻找与点P相关的两条向量的共线关系
题型1:用基底表示指定的向量
例1:(2009安徽卷理)给定两个长度为1的平面向量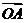 和
和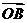 ,它们的夹角为
,它们的夹角为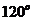 .如图所示,点C在以O为圆心的圆弧
.如图所示,点C在以O为圆心的圆弧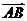 上变动.
上变动.
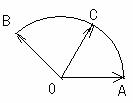 若
若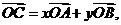 其中
其中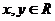 ,则
,则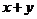 的最大值是________.
的最大值是________.
答案:2
例2: (08湖南理)设D、E、F分别是△ABC的三边BC、CA、AB上的点,且
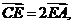
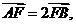 设
设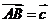 ,
,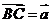 ,
,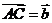 则
则 用
用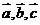 表示为______
表示为______
答案: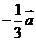
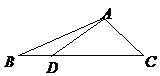 例3:(07天津文理15)
如图,在
例3:(07天津文理15)
如图,在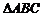 中,
中,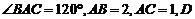 是边
是边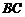 上一点,
上一点,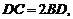 则
则
 .
.
[答案]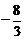
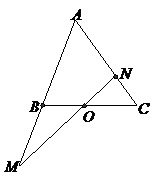 例4:(07江西理15)如图,在
例4:(07江西理15)如图,在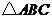 中,点
中,点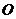 是
是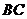 的中点,过点
的中点,过点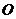 的直线分别交直线
的直线分别交直线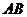 ,
,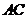 于不同的两点
于不同的两点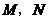 ,若
,若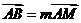 ,
,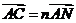 ,则
,则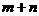 的值为______
的值为______
答案:2
题型2:根据向量条件,确定点P的位置.
例5: (2006陕西卷) 已知非零向量与满足(+)·=0且·= , 则△ABC为________三角形
答案:等边
例6:(07北京理4改)已知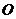 是
是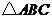 所在平面内一点,
所在平面内一点,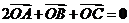 ,那么
,那么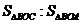 =______
=______
答案:2
例7:(2005全国I改)点O是三角形ABC所在平面内的一点,满足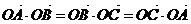 ,则点O是
,则点O是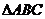 的_______心.
的_______心.
答案:垂心
三角函数概念、同角三角函数关系部分补充问题
复习目标:
11.(07江苏8)设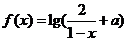 是奇函数,则使
是奇函数,则使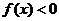 的
的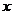 的取值范围是( )
的取值范围是( )
A.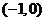 B.
B.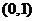 C.
C.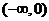 D.
D.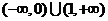
点评:奇函数如果在x=0处有定义,则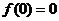
12(08安徽卷理)若函数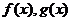 分别是
分别是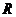 上的奇函数、偶函数,且满足
上的奇函数、偶函数,且满足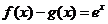 ,则有( )
,则有( )
A.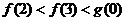 B.
B.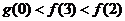
C.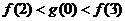 D.
D.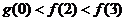
点评:运用奇偶性解函数方程组,需构造两个方程!
题型4:解答题:
13(2002上海春,20)已知函数f(x)=ax+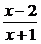 (a>1).
(a>1).
(1)证明:函数f(x)在(-1,+∞)上为增函数;
点评:两个不相干的函数的和函数的单调性问题,一定是它们具有相同的奇偶性!
10.(05江西卷)若函数 是奇函数,则a=
.
是奇函数,则a=
.
9.(08天津卷理)设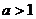 ,若仅有一个常数c使得对于任意的
,若仅有一个常数c使得对于任意的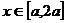 ,都有
,都有 满足方程
满足方程 ,这时,
,这时,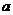 的取值的集合为
的取值的集合为
点评:理解题意与恰当转化是解题的关键!
题型3:有关奇偶性问题:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com