
重点: 理解并掌握弧度制定义;熟练地进行角度制与弧度制地互化换算;弧度制的运用.
难点: 理解弧度制定义,弧度制的运用.
3、情态与价值
通过本节的学习,使同学们掌握另一种度量角的单位制---弧度制,理解并认识到角度制与弧度制都是对角度量的方法,二者是辨证统一的,而不是孤立、割裂的关系.角的概念推广以后,在弧度制下,角的集合与实数集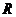 之间建立了一一对应关系:即每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应,为下一节学习三角函数做好准备.
之间建立了一一对应关系:即每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应,为下一节学习三角函数做好准备.
2、过程与方法
创设情境,引入弧度制度量角的大小,通过探究理解并掌握弧度制的定义,领会定义的合理性.根据弧度制的定义推导并运用弧长公式和扇形面积公式.以具体的实例学习角度制与弧度制的互化,能正确使用计算器.
1、知识与技能
(1)理解并掌握弧度制的定义;(2)领会弧度制定义的合理性;(3)掌握并运用弧度制表示的弧长公式、扇形面积公式;(4)熟练地进行角度制与弧度制的换算;(5)角的集合与实数集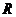 之间建立的一一对应关系.(6) 使学生通过弧度制的学习,理解并认识到角度制与弧度制都是对角度量的方法,二者是辨证统一的,而不是孤立、割裂的关系.
之间建立的一一对应关系.(6) 使学生通过弧度制的学习,理解并认识到角度制与弧度制都是对角度量的方法,二者是辨证统一的,而不是孤立、割裂的关系.
2.多举出一些日常生活中的“大于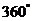 的角和负角”的例子,熟练掌握他们的表示,
的角和负角”的例子,熟练掌握他们的表示,
进一步理解具有相同终边的角的特点.
1.作业:习题1.1 A组第1,2,3题.
8.学习小结
(1) 你知道角是如何推广的吗?
(2) 象限角是如何定义的呢?
(3) 你熟练掌握具有相同终边角的表示了吗?会写终边落在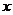 轴、
轴、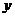 轴、直
轴、直
线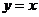 上的角的集合.
上的角的集合.
7.[展示投影]练习
教材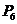 第3、4、5题.
第3、4、5题.
注意: (1)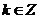 ;(2)
;(2)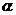 是任意角(正角、负角、零角);(3)终边相同的角不一定相等;但相等的角,终边一定相同;终边相同的角有无数多个,它们相差
是任意角(正角、负角、零角);(3)终边相同的角不一定相等;但相等的角,终边一定相同;终边相同的角有无数多个,它们相差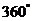 的整数倍.
的整数倍.
6.[展示投影]例题讲评
例1. 例1在 范围内,找出与
范围内,找出与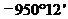 角终边相同的角,并判定它是第几象限角.(注:
角终边相同的角,并判定它是第几象限角.(注: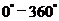 是指
是指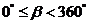 )
)
例2.写出终边在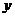 轴上的角的集合.
轴上的角的集合.
例3.写出终边直线在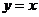 上的角的集合
上的角的集合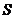 ,并把
,并把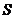 中适合不等式
中适合不等式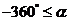
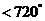 的元素
的元素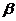 写出来.
写出来.
5.探究:将角按上述方法放在直角坐标系中后,给定一个角,就有唯一的一条终边与之对应.反之,对于直角坐标系中任意一条射线 (如图1.1-5),以它为终边的角是否唯一?如果不惟一,那么终边相同的角有什么关系?请结合4.(2)口答加以分析.
(如图1.1-5),以它为终边的角是否唯一?如果不惟一,那么终边相同的角有什么关系?请结合4.(2)口答加以分析.
[展示课件]不难发现,在教材图1.1-5中,如果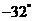 的终边是
的终边是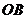 ,那么
,那么 角的终边都是
角的终边都是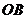 ,而
,而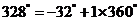 ,
,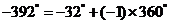 .
.
设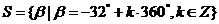 ,则
,则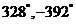 角都是
角都是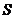 的元素,
的元素,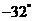 角也是
角也是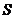 的元素.因此,所有与
的元素.因此,所有与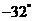 角终边相同的角,连同
角终边相同的角,连同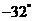 角在内,都是集合
角在内,都是集合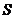 的元素;反过来,集合
的元素;反过来,集合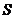 的任一元素显然与
的任一元素显然与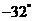 角终边相同.
角终边相同.
一般地,我们有:所有与角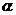 终边相同的角,连同角
终边相同的角,连同角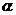 在内,可构成一个集合
在内,可构成一个集合
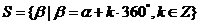 ,即任一与角
,即任一与角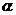 终边相同的角,都可以表示成角
终边相同的角,都可以表示成角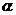 与整数个周角的和.
与整数个周角的和.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com