
9.练习
教材 .
.
8.例题讲评
例3.利用弧度制证明下列关于扇形的公式:
(1)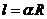 ; (2)
; (2)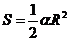 ; (3)
; (3) .
.
其中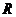 是半径,
是半径,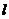 是弧长,
是弧长, 为圆心角,
为圆心角, 是扇形的面积.
是扇形的面积.
例4.利用计算器比较 和
和 的大小.
的大小.
注意:弧度制定义的理解与应用,以及角度与弧度的区别.
7. 填写特殊角的度数与弧度数的对应表:
|
度 |
 |
 |
 |
|
|
 |
 |
 |
|
|
 |
|
弧度 |
|
|
|
 |
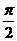 |
|
|
|
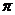 |
 |
|
角的概念推广以后,在弧度制下,角的集合与实数集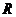 之间建立了一一对应关系:即每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
之间建立了一一对应关系:即每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.
6.例题讲解
例1.按照下列要求,把 化成弧度:
化成弧度:
(1) 精确值;
(2) 精确到0.001的近似值.
例2.将3.14 换算成角度(用度数表示,精确到0.001).
换算成角度(用度数表示,精确到0.001).
注意:角度制与弧度制的换算主要抓住 ,另外注意计算器计算非特殊角的方法.
,另外注意计算器计算非特殊角的方法.
5.根据探究中 填空:
填空:
 ,
, 度
度
显然,我们可以由此角度与弧度的换算了.
4.思考:如果一个半径为 的圆的圆心角
的圆的圆心角 所对的弧长是
所对的弧长是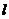 ,那么
,那么 的弧度数是多少?
的弧度数是多少?
角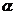 的弧度数的绝对值是:
的弧度数的绝对值是: ,其中,l是圆心角所对的弧长,
,其中,l是圆心角所对的弧长, 是半径.
是半径.
3.探究:如图,半径为 的圆的圆心与原点重合,角
的圆的圆心与原点重合,角 的终边与
的终边与 轴的正半轴重合,交圆于点
轴的正半轴重合,交圆于点 ,终边与圆交于点
,终边与圆交于点 .请完成表格.
.请完成表格.

弧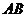 的长 的长 |
 旋转的方向 旋转的方向 |
 的弧度数 的弧度数 |
 的度数 的度数 |
 |
逆时针方向 |
|
|
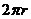 |
逆时针方向 |
|
|
 |
|
 |
|
 |
|
 |
|
|
|
|
 |
|
|
|
|
 |
|
|
|
|
|
 |
|
|
|
|
 |
我们知道,角有正负零角之分,它的弧度数也应该有正负零之分,如-π,-2π等等,一般地, 正角的弧度数是一个正数,负角的弧度数是一个负数,零角的弧度数是0,角的正负主要由角的旋转方向来决定.
2.弧度制的定义
[展示投影]长度等于半径长的圆弧所对的圆心角叫做1弧度角,记作1 ,或1弧度,或1(单位可以省略不写).
,或1弧度,或1(单位可以省略不写).
[创设情境]
有人问:海口到三亚有多远时,有人回答约250公里,但也有人回答约160英里,请问那一种回答是正确的?(已知1英里=1.6公里)
显然,两种回答都是正确的,但为什么会有不同的数值呢?那是因为所采用的度量制不同,一个是公里制,一个是英里制.他们的长度单位是不同的,但是,他们之间可以换算:1英里=1.6公里.
在角度的度量里面,也有类似的情况,一个是角度制,我们已经不再陌生,另外一个就是我们这节课要研究的角的另外一种度量制---弧度制.
[探究新知]
1.角度制规定:将一个圆周分成360份,每一份叫做1度,故一周等于360度,平角等于180度,直角等于90度等等.
弧度制是什么呢?1弧度是什么意思?一周是多少弧度?半周呢?直角等于多少弧度?弧度制与角度制之间如何换算?请看课本 ,自行解决上述问题.
,自行解决上述问题.
在我们所掌握的知识中,知道角的度量是用角度制,但是为了以后的学习,我们引入了弧度制的概念,我们一定要准确理解弧度制的定义,在理解定义的基础上熟练掌握角度制与弧度制的互化.
教学用具:计算器、投影机、三角板
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com