
1.作业:习题1.2 A组第1,2题.
11.学习小结
(1)本章的三角函数定义与初中时的定义有何异同?
(2)你能准确判断三角函数值在各象限内的符号吗?
(3)请写出各三角函数的定义域;
(4)终边相同的角的同一三角函数值有什么关系?你在解题时会准确熟练应用公式一吗?
10.巩固练习 第4,5,6,7题
第4,5,6,7题
9.例题讲评
例4.确定下列三角函数值的符号,然后用计算器验证:
(1)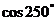 ; (2)
; (2)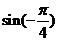 ; (3)
; (3)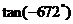 ; (4)
; (4)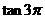
例5.求下列三角函数值:
(1)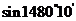 ; (2)
; (2)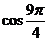 ; (3)
; (3)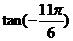
利用公式一,可以把求任意角的三角函数值, 转化为求 到
到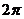 (或
(或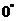 到
到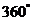 )角的三角函数值. 另外可以直接利用计算器求三角函数值,但要注意角度制的问题.
)角的三角函数值. 另外可以直接利用计算器求三角函数值,但要注意角度制的问题.
8.思考:根据三角函数的定义,终边相同的角的同一三角函数值有和关系?
显然: 终边相同的角的同一三角函数值相等.即有公式一:
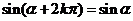
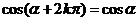 (其中
(其中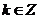 )
)
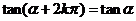
7.例题讲评
例3.求证:当且仅当不等式组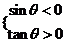 成立时,角
成立时,角 为第三象限角.
为第三象限角.
6.探究:请根据任意角的三角函数定义,将正弦、余弦和正切函数的定义域填入下表;再将这三种函数的值在各个象限的符号填入表格中:
|
三角函数 |
定义域 |
第一象限 |
第二象限 |
第三象限 |
第四象限 |
|
|
角度制 |
弧度制 |
|||||
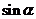 |
|
|
|
|
|
|
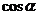 |
|
|
|
|
|
|
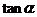 |
|
|
|
|
|
|
5.巩固练习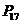 第1,2,3题
第1,2,3题
4.例题讲评
例1.求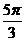 的正弦、余弦和正切值.
的正弦、余弦和正切值.
例2.已知角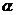 的终边过点
的终边过点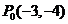 ,求角
,求角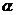 的正弦、余弦和正切值.
的正弦、余弦和正切值.
教材给出这两个例题,主要是帮助理解任意角的三角函数定义.我也可以尝试其他方法:
如例2:设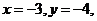 则
则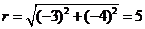 .
.
于是 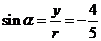 ,
,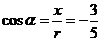 ,
,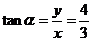 .
.
3.思考:如果知道角终边上一点,而这个点不是终边与单位圆的交点,该如何求它的三角函数值呢?
前面我们已经知道,三角函数的值与点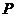 在终边上的位置无关,仅与角的大小有关.我们只需计算点到原点的距离
在终边上的位置无关,仅与角的大小有关.我们只需计算点到原点的距离 ,那么
,那么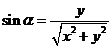 ,
,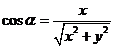 ,
,
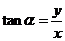 .所以,三角函数是以为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,又因为角的集合与实数集之间可以建立一一对应关系,故三角函数也可以看成实数为自变量的函数.
.所以,三角函数是以为自变量,以单位圆上点的坐标或坐标的比值为函数值的函数,又因为角的集合与实数集之间可以建立一一对应关系,故三角函数也可以看成实数为自变量的函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com