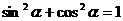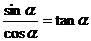重点：公式及的推导及运用：(1)已知某任意角的正弦、余弦、正切值中的一个，求其余两个；(2)化简三角函数式；(3)证明简单的三角恒等式.

难点: 根据角α终边所在象限求出其三角函数值；选择适当的方法证明三角恒等式.

3、情态与价值

通过本节的学习，牢固掌握同角三角函数的三个关系式并能灵活运用于解题，提高学生分析，解决三角问题的能力；进一步树立化归思想方法和证明三角恒等式的一般方法.

2、过程与方法

由圆的几何性质出发,利用三角函数线,探究同一个角的不同三角函数之间的关系；学习已知一个三角函数值，求它的其余各三角函数值；利用同角三角函数关系式化简三角函数式；利用同角三角函数关系式证明三角恒等式等.通过例题讲解，总结方法.通过做练习,巩固所学知识.

1、知识与技能

(1) 使学生掌握同角三角函数的基本关系；(2)已知某角的一个三角函数值，求它的其余各三角函数值；(3)利用同角三角函数关系式化简三角函数式；(4)利用同角三角函数关系式证明三角恒等式；(5)牢固掌握同角三角函数的三个关系式并能灵活运用于解题，提高学生分析，解决三角问题的能力；(6)灵活运用同角三角函数关系式的不同变形，提高三角恒等变形的能力，进一步树立化归思想方法；(7)掌握恒等式证明的一般方法.

2．练习三角函数线的作图.

1．　 作业：

　比较下列各三角函数值的大小(不能使用计算器)

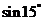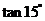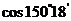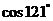(1)、　 (2)、　 (3)、

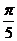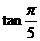
8.练习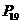第1,2,3,4题

9学习小结

(1)了解有向线段的概念.

(2)了解如何利用与单位圆有关的有向线段，将任意角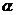的正弦、余弦、正切函数值分别用正弦线、余弦线、正切线表示出来.

(3)体会三角函数线的简单应用.

[评价设计]

7.例题讲解

例1．已知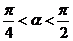，试比较的大小.

处理:师生共同分析解答,目的体会三角函数线的用处和实质.

6.探究：(1)当角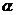的终边在第二、第三、第四象限时，你能分别作出它们的正弦线、余弦线和正切线吗？

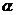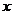(2)当的终边与轴或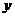轴重合时，又是怎样的情形呢？

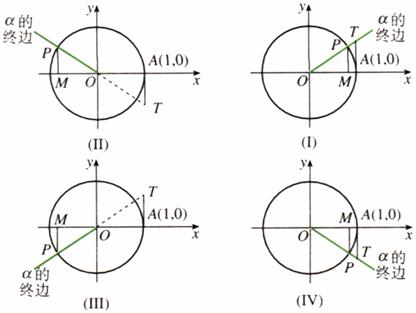
5.如何用有向线段来表示角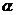的正切呢?

如上图,过点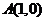作单位圆的切线,这条切线必然平行于轴,设它与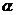的终边交于点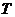,请根据正切函数的定义与相似三角形的知识,借助有向线段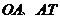,我们有

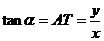
我们把这三条与单位圆有关的有向线段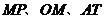,分别叫做角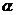的正弦线、余弦线、正切线，统称为三角函数线.